ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА.
Дифференциальное уравнение второго порядка имеет вид  .
.
Определение. Общим решением уравнения второго порядка называется такая функция 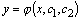 , которая при любых значениях
, которая при любых значениях 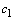 и
и 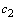 является решением этого уравнения.
является решением этого уравнения.
Определение. Линейным однородным уравнением второго порядка называется уравнение 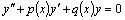 . Если коэффициенты
. Если коэффициенты 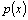 и
и 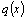 постоянны, т.е. не зависят от
постоянны, т.е. не зависят от 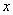 , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:
, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: 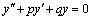 .
.
Уравнение  будем называть линейным неоднородным уравнением.
будем называть линейным неоднородным уравнением.
Определение. Уравнение  , которое получается из линейного однородного уравнения заменой функции
, которое получается из линейного однородного уравнения заменой функции 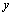 единицей, а
единицей, а  и
и  - соответствующими степенями
- соответствующими степенями 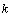 , называется характеристическим уравнением.
, называется характеристическим уравнением.
Известно, что квадратное уравнение  имеет решение, зависящее от дискриминанта
имеет решение, зависящее от дискриминанта 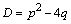 :
: 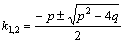
 , т.е. если
, т.е. если 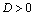 , то корни
, то корни 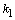 и
и 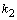 - действительные различные числа. Если
- действительные различные числа. Если  , то
, то 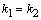 . Если же
. Если же 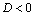 , т.е.
, т.е. 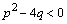 , то
, то 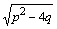 будет мнимым числом, а корни
будет мнимым числом, а корни 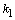 и
и 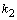 - комплексными числами. В этом случае условимся обозначать
- комплексными числами. В этом случае условимся обозначать  .
.
Пример 4. Решить уравнение 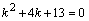 .
.
Решение. Дискриминант этого квадратного уравнения  , поэтому
, поэтому 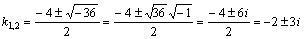 .
.
Покажем, как по виду корней характеристического уравнения найти общее решение однородного линейного уравнения второго порядка.
Если  - действительные корни характеристического уравнения, то
- действительные корни характеристического уравнения, то 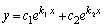 .
.
Если корни характеристического уравнения одинаковы, т.е. 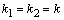 , то общее решение дифференциального уравнения ищут по формуле
, то общее решение дифференциального уравнения ищут по формуле 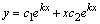 или
или 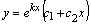 .
.
Если же характеристическое уравнение имеет комплексные корни  , то
, то  .
.
Пример 5. Найти общее решение уравнения 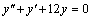 .
.
Решение. Составим характеристическое уравнение для данного дифференциального уравнения:  . Его корни
. Его корни  ,
,  действительны и различны. Поэтому общее решение
действительны и различны. Поэтому общее решение 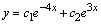 .
.
Пример 6. Решить уравнение  .
.
Решение. Характеристическое уравнение 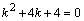 или
или  имеет корни
имеет корни  . Так что
. Так что 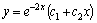 .
.
Пример 7. Решить уравнение 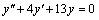 .
.
Решение. Характеристическое уравнение 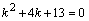 данного однородного линейного уравнения мы уже решили выше в примере 4. Корни этого уравнения
данного однородного линейного уравнения мы уже решили выше в примере 4. Корни этого уравнения 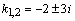 , поэтому общее решение линейного однородного уравнения находим по формуле
, поэтому общее решение линейного однородного уравнения находим по формуле  , где
, где 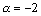 ,
, 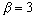 . Итак,
. Итак, 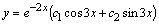 .
.
Общее решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами, т.е. уравнения вида  , записывается в виде
, записывается в виде 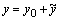 , где
, где 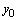 - общее решение соответствующего однородного уравнения, а
- общее решение соответствующего однородного уравнения, а  - какое-либо частное решение неоднородного уравнения.
- какое-либо частное решение неоднородного уравнения.
Укажем способ, позволяющий найти частное решение неоднородного уравнения по виду правой части. Заметим, что это возможно лишь в случаях, когда правая часть уравнения является функцией определенного вида.
1. Пусть 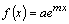 , где
, где 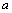 - некоторое число, не равное нулю. Тогда
- некоторое число, не равное нулю. Тогда
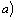 если,
если, 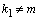 ,
, 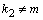 , то частное решение уравнения ищут в виде
, то частное решение уравнения ищут в виде 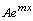 , где
, где  - неизвестное число, которое находят, подставляя
- неизвестное число, которое находят, подставляя 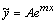 в неоднородное уравнение;
в неоднородное уравнение;
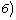 если
если  , а
, а 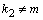 , то в этом случае частное решение ищут в виде
, то в этом случае частное решение ищут в виде 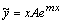 ;
;
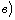 наконец, если и
наконец, если и  и
и 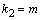 , т.е.
, т.е. 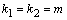 , то
, то  .
.
2. Если  , где
, где 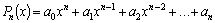 – многочлен степени
– многочлен степени 
 , то
, то
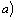 при
при 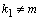 ,
, 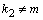 решение ищут, просто «передразнивая» правую часть, т.е.
решение ищут, просто «передразнивая» правую часть, т.е. 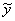 , как и правая часть, должна представлять собой произведение многочлена той же степени, что и в правой части уравнения, но с неопределенными коэффициентами, и
, как и правая часть, должна представлять собой произведение многочлена той же степени, что и в правой части уравнения, но с неопределенными коэффициентами, и 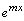 , т.е.
, т.е. 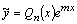 . В частности, если
. В частности, если 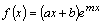 , то
, то  ;
;
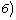 при
при  ,
, 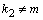 частное решение
частное решение  ищут в виде
ищут в виде  ;
;
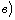 при
при 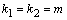 находим
находим  по формуле
по формуле 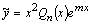 .
.
2. Пусть теперь 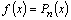 , т.е. в правой части уравнения находится многочлен некоторой степени или некоторое число (если степень многочлена нулевая). Тогда мы можем воспользоваться формулами, рассмотренными выше, полагая в них
, т.е. в правой части уравнения находится многочлен некоторой степени или некоторое число (если степень многочлена нулевая). Тогда мы можем воспользоваться формулами, рассмотренными выше, полагая в них 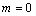 . (Действительно
. (Действительно 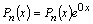 и, очевидно,
и, очевидно, 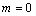 ).
).
Таким образом, имеем:
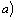 если
если 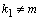 ,
, 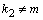 , то
, то 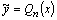 ;
;
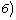 если
если  ,
, 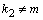 , то
, то 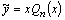 ;
;
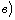 если
если 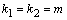 , то
, то 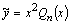 .
.
Пример 8. Решить уравнение  .
.
Решение. Составим характеристическое уравнение соответствующего данному уравнению однородного уравнения  :
:  . Корни этого уравнения
. Корни этого уравнения 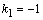 и
и 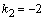 действительны и различны, поэтому общее решение соответствующего однородного уравнения имеет вид
действительны и различны, поэтому общее решение соответствующего однородного уравнения имеет вид 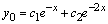 . Составим частное решение
. Составим частное решение  неоднородного уравнения по виду правой части:
неоднородного уравнения по виду правой части:  . Среди корней характеристического уравнения нет равных числу
. Среди корней характеристического уравнения нет равных числу 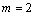 . Поэтому ищем частное решение
. Поэтому ищем частное решение  в виде
в виде  , где
, где  - неопределенный коэффициент, который находим, подставляя
- неопределенный коэффициент, который находим, подставляя  в исходное уравнение. Найдем
в исходное уравнение. Найдем 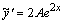 ,
,  и подставим
и подставим  ,
, 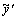 и
и  в уравнение. Имеем
в уравнение. Имеем 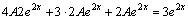 . Далее соберем подобные в левой части уравнения и разделим обе части уравнения на
. Далее соберем подобные в левой части уравнения и разделим обе части уравнения на  :
: 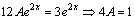 , откуда
, откуда  . Подставим найденное
. Подставим найденное  в
в  . Тогда
. Тогда 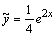 .
.
Складывая общее решение однородного уравнения и найденное частное решение неоднородного уравнения, получим 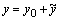 :
:  .
.
Пример 9. Решить уравнение 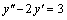 .
.
Решение. Составим характеристическое уравнение соответствующего однородного уравнения  . Получим квадратное уравнение
. Получим квадратное уравнение  .
. 

Его корни 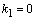 ,
, 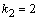 , так что общее решение однородного уравнения получим в виде
, так что общее решение однородного уравнения получим в виде 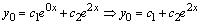 .
.
Правая часть уравнения 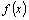 представляет собой многочлен нулевой степени или число, равное трем. В этом случае, «передразнивая» правую часть, мы должны и решение
представляет собой многочлен нулевой степени или число, равное трем. В этом случае, «передразнивая» правую часть, мы должны и решение  неоднородного уравнения искать в виде числа. Но среди корней характеристического уравнения имеется
неоднородного уравнения искать в виде числа. Но среди корней характеристического уравнения имеется  , поэтому
, поэтому 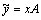 .
.
Найдем неизвестный коэффициент  , подставляя
, подставляя  в уравнение. Для этого найдем
в уравнение. Для этого найдем 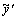 и
и 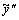 :
: 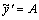 ,
,  . Тогда получим
. Тогда получим 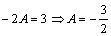 и
и 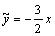 , а общее решение неоднородного уравнения получим, складывая
, а общее решение неоднородного уравнения получим, складывая  и
и  . Окончательно
. Окончательно 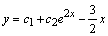 .
.

