Нормальное уравнение прямой. Расстояние от точки до прямой

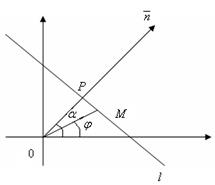Пусть дана прямая L. Проведем через начало координат прямую, перпендикулярную L: n – нормаль. На нормали введем положительное направление- от (·) 0 к (·) Р. – угол от оси ОХ до направления нормали, p – длина ОР. Считая и p известными, выведем уравнение прямой. Возьмем на прямой (·)М (х; у). Очевидно, что . Пусть полярные координаты = 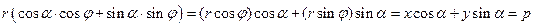или – нормальное уравнение прямой (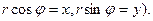

 

Расстояние от (·) до прямой. Пусть L – прямая в нормальном виде . (·) Мо (xo, yo) – лежит вне прямой. Определим d – расстояние от (·) Мо до прямой L. Через Мо проведем прямую Lо, параллельную L. Nо – (·) пересечения Lо с нормалью.

а) если Nо лежит по ту же сторону от 0, что и N, то нормальное уравнение прямой Lо: 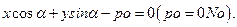т.к. то 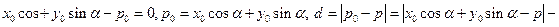расстояние.

б) если Nо лежит по другую сторону от О, то уравнение прямой Lо:

.

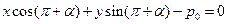
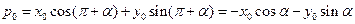Приведение общего уровня к нормальному. Пусть – общее уравнение, а – ее нормальное уравнение, т.к. эти уравнения определяют одну прямую, то их коэффициенты пропорциональны. Умножим все члены общего уровня на первые два возведем в квадрат и сложим: < 0, поэтому знак берется противоположным знаку С. – нормирующий множитель.

Пример. Дана прямая 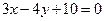и (·) М (4; 3). Найти расстояние d от М до прямой.

Приведем уравнение к нормальному виду:

.

 

 

Общее уравнение плоскости. Неполные уравнения плоскости. Уравнение плоскости в отрезках

Теорема. В декартовых координатах каждая плоскость определяется уравнением первой степени.

Возьмем на плоскости , выберем нормальный вектор 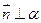, 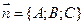. Пусть – произвольная точка на плоскости. Тогда , 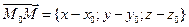. Тогда , – уравнение плоскости, проходящей через . Раскроем скобки: , – общее уравнение плоскости, где .

Справедливо и обратное: каждое уравнение первой степени определяет плоскость.

Рассмотрим некоторые частные случаи полученного уравнения.

– параллельна оси ОХ.

– параллельна оси ОY.

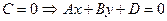– параллельна оси ОZ.

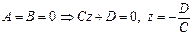– плоскость параллельна плоскости XOY

– плоскость параллельна плоскости XOY

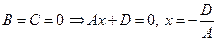– плоскость параллельно плоскости YOZ

D = 0 => плоскость проходит через начало координат.

 

Уравнение плоскости в отрезках.

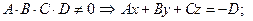
. Обозначим – уравнение плоскости в отрезках. Смысл величин а, b, c – это отрезки, которые плоскость отсекает от осей координат.

 

Нормальное уравнение плоскости. Расстояние от точки до плоскости

Рассмотрим величину 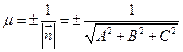, μ – нормирующий множитель. Умножим обе части общего уравнения плоскости на μ . Получим . Коэффициенты при x, y, z являются направляющими косинусами вектора нормами плоскости: , , , где α , ß , γ – углы, которые нормаль образует с координатными осями.

Обозначим . Получим – нормальное уравнение плоскости.

Расстояние от точки до плоскости

 

Пусть уравнение плоскости Р : Ax + By + Cz + D = 0, дана (∙ ) , которая не принадлежит плоскости. Тогда . Чтобы найти расстояние от точки до плоскости, следует подставить координаты этой точки в уравнение плоскости и полученную величину поделить на модуль вектора , т.е. на нормирующий множитель μ . Для определения расстояния от точки до плоскости можно пользоваться нормальным уравнением плоскости. В этом случае .

 

 

Уравнение плоскости, проходящей через 3 данных точки. Угол между плоскостями

Пусть точки лежат в плоскости Р и точка – любая точка плоскости. Тогда , , лежат в одной плоскости и являются компланарными. Условие компланарности: равенство нулю смешенного произведения: , т.е.

—уравнение плоскости, проходящей через 3 точки.

Взаимное расположение 2-х плоскостей

 

Пусть плоскости Р₁ и Р₂ заданы общими уравнениями , . Соответственно векторы 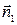и 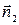этих плоскостей , . Угол между плоскостями равен углу между нормалями, который можно найти по формуле , .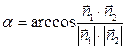

Плоскости параллельны, если 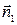|| 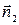, следовательно .

Плоскости перпендикулярны, если .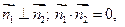

 

Прямая в пространстве

 

В общем случае прямую в пространстве можно рассматривать как линию пересечения 2-х плоскостей: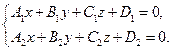

Канонические уравнения прямой

Пусть (∙ ) М₀(x₀; y₀; z₀) – точка лежащая на прямой; 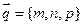, где m, n, p – координаты направляющего вектора прямой, т.е. вектора параллельного данной прямой. М (x; y; z) – текущая точка. 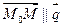, получаем уравнение 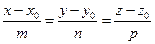– канонические уравнения прямой.

Чтобы перейти от общего уравнения прямой к каноническому, в качестве точки М₀берут любое решение системы, направляющий вектор прямой можно найти как векторное произведение векторов нормалей × .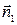

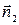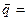
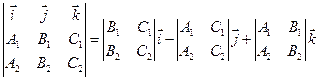. Если направляющий вектор прямой задан точками M₁, M₂, то можно записать уравнение прямой, проходящей через 2 данные точки , : .

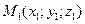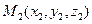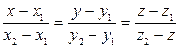Угол между прямыми

Пусть 2 прямые заданы в канонической форме, т.е. известны направляющие векторы каждой прямой: , .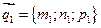

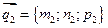Угол 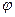между прямыми равен углу между направляющими векторами: .

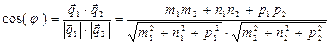Если прямые параллельны, то 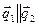и .

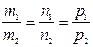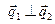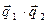Если прямые перпендикулярны, , то =0 и 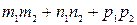= 0 – условия перпендикулярности прямых.

 

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться: