Представление комплексных чисел

Алгебраическая форма

Запись комплексного числа 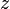в виде , , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ):

Тригонометрическая и показательная формы

Если вещественную и мнимую части комплексного числа выразить через модуль и аргумент ( 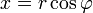, ), то всякое комплексное число 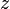, кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где 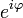— расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

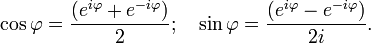
Формула Муавра и извлечение корней из комплексных чисел

Основная статья: Формула Муавра

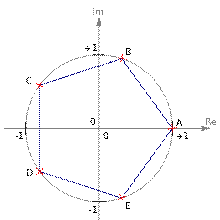
Корни пятой степени из единицы(вершины пятиугольника)

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где — модуль, а — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней -ой степени из ненулевого комплексного числа:

Отметим, что корни -й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса с центром в начале координат (см. рисунок).

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту стригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа выполнено следующее равенство:

,

где — основание натурального логарифма,

— мнимая единица.

Доказательство

Доказательство формулы Эйлера можно провести с использованием рядов Тейлора. Разложим функцию в ряд Тейлора по степеням . Получим:

Но

Поэтому

 

53.МОМЕНТ ИНЕРЦИИ КОНУСА

J = ∫ r^2*dm(r)- интеграл момента инерции
A=H/R - тангенс угла наклона образующей конуса
h(r)=A*(R-r)*r - зависимость высоты цилиндра от его радиуса
dm(r)=p*2*Pi*r*h(r)*dr - дифференциал массы цилиндра толщиныой dr
J = ∫ A*p*2*Pi*r*(R-r)*r*r^2*dr -интеграл момента инерции цилинра переменных радиуса и высоты, выраженной через текущий радиус
J = A*p*2*Pi* ∫ r^4*(R-r)*dr
∫ r^4*(R-r)*dr = R^4*R/4-R^5/5 = R^5/20
J = A*p*Pi*R^5/10
V = Pi*R^2*H/3 - объем конуса из школьной геометрии
H=A*R - тангенс угла наклона образующей конуса
m = p*Pi*A*R^3/3- масса через плотность и объем
p = 3*m/(A*Pi*R^3) - плотность для выражения ее в формуле момента инерции через массу
Окончательно: J=3*m*R^2/10

54.МОМЕНТ ИНЕРЦИИ СФЕРЫ

Сразу выразим плотность через массу 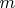и объем сферы cреднего радиуса малой толщины :
(объем тонкой сферы = пл.сферы на ее толщину).
Интегрируем произведение масс колец (плотности , длины , толщины , ширины ) на квадрат расстояния от оси
Дифференциал мом. инерции

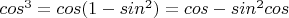
Интеграл этой функции
интеграл момента инерции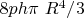
Подставим вместо плотности и получим итог:
.

Будем считать что функция плотности задана на поверхности и за ось примем . Площадь сферы обозначим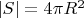
Переходим к цилиндрическим координатам:
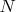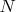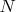Мысленно разбиваем диаметр вдоль оси на равных отрезков и получаем соответственно разбиение сферы на сферических поясов (и шапочки на полюсах) одинаковой высоты . Далее проводим меридианов и соответственно разбиваем каждый сферический пояс на сферические " квадраты" ( в полюсах- треугольники) каждый с угловой мерой . Получаем в общей сложности кусочков.

В каждом кусочке /элементе сферы - выбираем точку с координатами 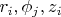, и находим значение плотности Момент каждого кусочка относительно оси приблизительно равен

Чтобы найти площадь кривой поверхности, вообще говоря необходимо привлекать частные производные, но в нашем случае (сферы) спасает теорема, утверждающая, что если сферические пояса имеют одинаковую высоту, то их площади равны. (Доказывается средствами матана 2 курса или просто смотри в инете ). Поэтому равны и площади всех элементов нашего разбиения сферы .

Далее все это суммируем по обоим индексам, устремляем 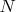к бесконечности и получаем двойной интеграл по поверхности как советовали в самом начале.

Ну а если, как частный случай, масса распределена равномерно, то вытаскивая за интегралы и умножив на получаем

где 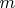- масса сферы.

 

 

 

 

 

 

 

 

 

⇐ Предыдущая123456789

Поделиться: