Локальное присваивание значений

Программа Mathcad — это обособленный модуль внутри документа Mathcad со
своими именами переменных и их значениями, которые не видны из других мест
документа.

Присваивание значений переменным и константам в программах производится
с помощью программного оператора присваивания (← ), который вводится с панели программирования щелчком на кнопке Local Definition (Локальное определение).
При создании программы, когда этот знак приходится использовать часто, полезно пользоваться клавишей ((открывающая фигурная скобка).

Локальные значения переменных нельзя использовать вне программы. Если это
все же необходимо, их надо вывести из программы специальным образом (см. раз-
дел «Вывод значений из программы»).

ВНИМАНИЕ: Ни «обычный» оператор присваивания (: =), ни оператор вывода (=) в пределах программ не применяются.

Из основного документа в программу передаются в виде констант все значения
величин, имеющих одинаковые имена. Эти значения сохраняются неизменными
при любых действиях с ними внутри программы.

В большой программе, например, в программе решения упругопластической задачи (пример 16 в части IV), где в головную программу ZZ надо передать много переменных величин, всем им в начале программы присваиваются значения. Обратите
внимание, что имена передаваемых и принимаемых величин чаще всего совпадают, чтобы программу было легче понять. В указанном примере передается 6 вели-
чин и каждая занимает одну строку в программе, что в значительной степени увеличивает программу.

Передать нужные величины в программу можно и другим способом, создав программу-функцию, где передаваемые величины заданы в виде параметров функции. Так оформлены в рассмотренном примере все подпрограммы, используемые
затем в главной программе. При этом программа занимает меньше места в длину,
но больше в ширину.

Для экономии места в документе можно прибегать к наложению объектов друг на
друга. Щелкните правой кнопкой мыши на объекте и выберите в контекстном меню команду Вringto Front (Выдвинуть на передний план) или Send to Back (Убрать на задний план). Документ получается более компактным. Именно так скомпонованы
многие программы в этой книге.

Любая программа представляет собой сочетание обычных математических выражений с операторами условия и цикла. Разберем действие этих операторов.

Условный оператор if.

Условный оператор if действует в два этапа. Сначала проверяется условие, записанное справа от оператора if, и, если оно истинно, выполняется выражение слева
от него, если ложно, происходит переход к следующей строке программы.

Чтобы вставить условный оператор if в программу, проделайте описанную ниже процедуру.
1. В создаваемой программе установите курсор на свободное место ввода, в которое должен быть вставлен условный оператор.

2. На панели программирования щелкните на кнопке If Statement (Оператор if).

В программе появится шаблон оператора с двумя местами ввода.

3. В правое место ввода введите условие. Пользуйтесь при этом логическими операторами, вводя их с панели Boolean (Булевы операторы).

4. Слева от оператора if введите выражение, которое должно выполняться, если условие истинно.

Рис. 6.2. Способ записи условия if в Mathcad.

Если при выполнении условия должно выполняться сразу несколько выражений,
то надо иметь несколько мест ввода. Для их создания установите курсор на место
ввода слева от оператора if и щелкните на кнопке Add Program Line (Добавить строку программы) панели программирования столько раз, сколько строк надо ввести.

Обратите внимание, что при этом меняется вид условного оператора. Новая вертикальная линия с местами ввода появляется не слева, а ниже и правее оператора if (рис 6.2.).

 

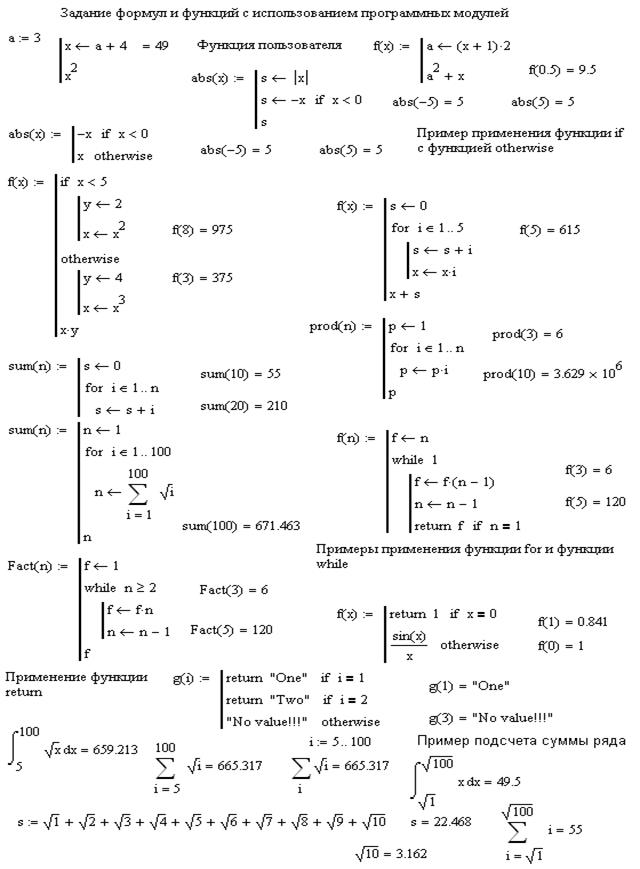
Рис. 6.3. Примеры записи операторов программирования.

Для примера рассмотрим решение задачи Коши для ДУ вида

у' = -x² + y

с начальным условием у(0) = 1.
Для реализации задания мы будем использовать пакет Mathcad. В пакете Mathcad соответствующие блоки будут выглядеть следующим образом:
1. x0: = 0 y0: = 1 задание начальных условий;

2. f(x, y): = -x² + y - запись самой функции, решение которой необходимо найти;

3. x1: = 10 - конечное значение интервала интегрирования;

N: =1000, - число итераций;

i: = 0..N, - т.е. индекс при x меняется от 0 до N;

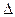= (х1 — х0)/N - цикл нахождения шага интегрирования;
4. x₁ = 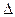x * i - нахождение значений x_i;
5. В данном блоке нам предстоит написать функцию, реализующую алгоритм Эйлера, которая будет состоять из нескольких операторов, т. е. является программой. Так как существуют определенные отличия средств создания программ пакета Mathcad от обычных языков программирования, необходимо, на примере решения данной задачи подробно описать последовательность действий, позволяющих создавать программы в пакете MathCAD.
В качестве входных параметров, передаваемых в данную функцию, будем использовать следующие:

значение функции в начальной точке у0 (см пункт 1); массив координат точек, в которых ищется решение ДУ (см. пункт 3); функцию f(х, у); N — количество точек, в которых ищется решение ДУ.
Для создания функции необходимо:
1) , затем — символ присваивания:
2) на втором - включить панель с набором инструментов программирования, нажав кнопку

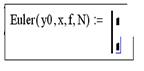3) нажать на панели программирования кнопку , в результате
в рабочем документе появится заготовка для ввода операторов, входящих в состав функции (можно также кнопкой ъ).

4) переместить курсор в первое поле ввода, щелкнув по нему мышью

и ввести y₀ затем нажать

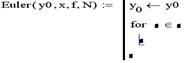кнопку «← » и ввести в появившееся поле у0: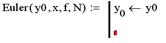
5) щелкнуть по кнопке «Add line»

6) и нажать кнопку «for»

 

7) ввести в соответствующие

местозаполнители: счетчик

цикла, диапазон
изменения счетчика
цикла и оператор, вы-
полняемый в цикле:

8) переместить кур-
сор в нижнее поле и
напечатать у:

6. Получить решение ДУ
в массив М (вывод решения): М: = Еu1ег(y0, x, f, N)
7. График решения ДУ (см. рис.6.4).

 

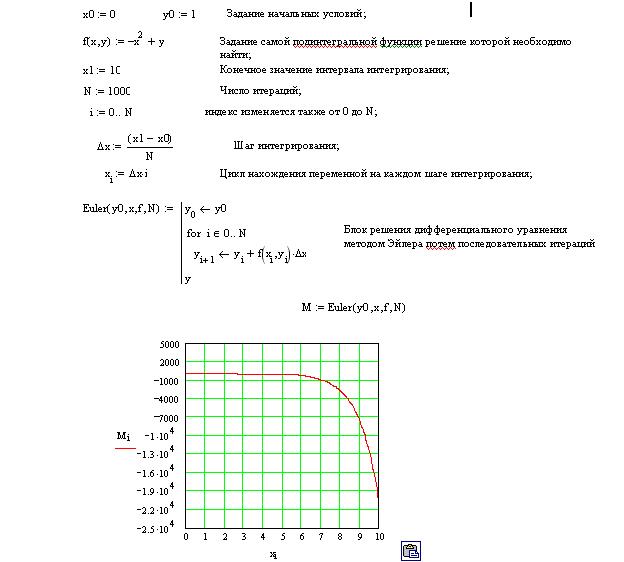
Рис.6.4. График решения уравнения.

 

Задание:

1. Решить дифференциальное уравнение первого порядка (ДУ), согласно варианту (см. таблицу 6-2), традиционным способом (аналитически).

2. Составить таблицу значений решения ДУ первого порядка, при различных значениях шага h, методом Эйлера в пакете MathCAD.

3. Поварьировать начальными условиями (x₀, y₀, x_n), чтобы выявить их влияние на решение ДУ.

4. На отдельном листе представить график решения ДУ в пакете MathCAD.

Таблица 6-2.

№№ п.п.	Дифференциальное уравнение	Начальное условие	Конечная Точка xn	Шаг h
x0	y0
	y’ = x*y2 + 1				0.1
	y’= x2*y3 + x2				0.1
	y’ = x + Sin y/π				0.1
	y’ = x + Sin y/√ 10	1.6	2.9	2.6	0.1
	y’ = x + Cos y/π	1.7	5.3	2.7	0.1
	y’= x + Cos y/3	1.6	4.6	2.6	0.1
	y’ = x2*y2 -1				0.1
	y’ = Sin y – Sin x				0.1
	y’ = 1 + x – x2 -2y2				0.1
	y’ = 0, 1*(x2 + y2)				0.1
	y’ = √ x *y2 + 1				0.1
	y’ = 1/(x2 + y2)				0.1
	y’ = x +Cos y/√ 7	0.5	0.6	1.5	0.1
	y’ = x + Cos y/e				0.1
	y’ = x + Sin y/3				0.1
	y’ = x + √ y	0.5	0.7	1.5	0.1
	y’ = √ x + √ y				0.1
	y’ = y3 -x			0.1	0.01
	y’ = ex – y2			0.4	0.04
	y’ = x2*y2 -1			0.1	0.01
	y’ = 0, 1(x2*y2 +1)				0.1
	y’ = x2 –xy + y2		0.1		0.1
	y’ = 0, 2(x2 – y3)				0.1
	y’ = 0, 1(x2 + y2)		0.1		0.1
	y’ = ex –y2			0.5	0.05
	y’ = x + y2				0.1
	y’ = x2 + y				0.1
	y’ = 2x – 0, 1y2				0.1
	y’ =0, 1x2 + y2		0.1		0.1
	y’ = 2x – y2				0.1
	y’ = x2 + 2√ y				0.1
	y’ = 2x2 + √ y				0.1
	y’ = 0, 2x + 3y2				0.2
	y’ = xy + y2		0.1		0.1
	y’ = Sin x + y		0.2		0.1
	y’ = x3 + y2				0.1
	y’ = 3√ x +√ y				0.1
	y’ = x + √ y				0.1
	y’ = x + Sin y/√ 5				0.1
	y’ = x + √ y				0.1
	y’ = √ y *y2 + 1				0.1
	y’ = x2 + y2 - 3				0.1

 

 

Назад

 

ЛАБОРАТ0РНАЯ РАБОТА № 7

⇐ Предыдущая234567891011Следующая ⇒

Поделиться: