Статические и динамические свойства динамических систем.

1. Статические и динамические модели
По признаку учета зависимости объекта моделирования от времени различают статические и динамические характеристики систем, отражаемые в соответствующих моделях.
Статические модели (модели статики) отражают функцию системы - конкретное состояние реальной или проектируемой системы (своего рода его «мгновенную фотографию»)
Примеры. Закон Ома, описание показателей эффективности организацией в некоторый момент времени.
Динамические модели (модели динамики) отражают функционирование системы - процесс изменения состояний реальной или проектируемой системы. Они показывают различия между состояниями, последовательность смены состояний и развитие событий с течением времени.
Примеры. Описание процесса изменения спроса на какой-либо товар под влиянием рекламы, изменение температуры электроплиты при ее включении, описание процесса изменения показателей эффективности за некоторый период времени.
Отличие статических и динамических моделей заключено в учете времени: в статике его как бы не существует, а в динамике это основной элемент.

2. Статические характеристики систем
В узком смысле к статической характеристике системы можно отнести ее структуру. Однако нас чаще будут интересовать свойства системы по преобразованию ходов и выходов (т.е. функция системы) в установившемся режиме, когда отсутствуют изменения значений как входных, так и выходных переменных. Такие свойства определяются как статические характеристики.
Статическая характеристика - это зависимость между входной и выходной величинами в установившемся режиме. Статическая характеристика может быть представлена:
o математической моделью вида Y = F(X)
o графической моделью.

3. Динамические характеристики систем
Следующий шаг в исследовании систем состоит в том, чтобы понять и описать, как система «работает», что происходит с ней самой и с окружающей средой в ходе реализации поставленной цели. Для описаний функционирования системы используются динамические модели.
Для разных объектов и систем разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, до формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля. Свойства динамических систем определяет динамические характеристики.

Динамическая характеристика - это реакция системы на возмущение (зависимость изменения выходных переменных входных и от времени).
Динамическая характеристика может быть представлена:
o математической моделью в виде дифференциального уравнения (или уравнений) вида:

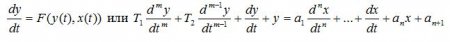
o математической моделью в виде решения дифференциального уравнения;
o графической моделью, состоящей из двух графиков: графика изменения возмущения во времени и графика реакции выхода на это возмущение - графической зависимости измене-ния выхода во времени.

Рис. 1. Статическая (а) и динамическая (б) характеристики электроплиты

4. Элементарные динамически звенья
При исследовании динамики систем часто невозможно составить математическое описание всей системы сразу. Для облегчения этой задачи систему разбивают на отдельные элементы и для каждого из них составляют дифференциальные уравнения, которые записываются на основе соответствующих физических законов. Для отображения динамических свойств элементов системы независимо от их физической природы используют понятие динамического звена.
Динамическое звено - это часть системы или элемента, описываемая определенным дифференциальным уравнением. Динамическим звеном можно представить элемент, совокупность эле-ментов, автоматическую систему в целом.
Любую динамическую систему можно условно разложить на динамические «атомы» - элементарные динамические звенья. Упрощенно элементарным динамическим звеном можно считать звено с одним входом и одним выходом (рис. 2).

 

Рис. 2. Элементарное динамическое звено.

 

Элементарное звено должно быть звеном направленного действия: звено передает воздействие только в одном направлении с входа на выход, так что изменение состояния звена не влияет на состояние предшествующего звена, работающего на вход. Поэтому при разбиении системы на звенья направленного действия математическое описание каждого звена может быть составлено без учета связей его с другими звеньями. Соответственно математическое описание всей системы в целом может быть получено как совокупность независимых друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связи между звеньями.
Дифференциальные уравнения элементов имеют порядок не выше второго, поэтому типовые звенья описываются дифференциальными уравнениями нулевого, первого и второго порядка. Таким образом, разновидностей элементарных динамических звеньев немного, и все многообразие конструктивных элементов схем с точки зрения общности их динамических характеристик можно свести к небольшому числу эквивалентных им звеньев. Для линейных систем можно выделить ограниченную совокупность элементарных динамических звеньев, которых образуют своего рода «таблицу Менделеева» динамики.

Все звенья различают по виду уравнений, определяющих характеристики переходных процессов, возникающих в них при одинаковых исходных условиях и одинаковом виде возмущения.
Для оценивания поведения элементарного звена обычно на его вход подают тестовые сигналы определенной формы. Наиболее часто используются такие виды возмущающих сигналов.
1. Ступенчатое воздействие (рис. 3, а):

Частым случаем ступенчатого воздействия является единичное воздействие, которое описывается так называемой единичной функцией: x(t)=l(t)

2. Импульсное воздействие (единичный импульс или дельта функция) x(t) = σ (t) (рис. 3, б):

Следует заметить, что δ (t) и единичная ступенчатая функция связаны соотношением:

Рис. 3. Воздействия: а- ступенчатое; б- импульсное.

3. Периодический сигнал: либо в виде синусоиды, либо в виде прямоугольной волны.

5. Виды типовых звеньев и их переходные функции
Воздействие на вход системы вызывает изменение ее выхода y(t) - переходный процесс, именуемый переходной функцией.
Переходная (временная) функция — это реакция выходной переменной звена на изменение входа.
В дальнейшем мы будем рассматривать типовые звенья и характер изменения их выходов при единичном ступенчатом возмущении. В частности, будем анализировать такие динамические характеристики каждого звена: дифференциальное уравнение, его описывающее, его частное решение и переходную функцию звена при единичном воздействии — кривую разгона h(t). Таким образом, h(t) = y(t) при x(t) = l(t).
В случае импульсного возмущения переходная характеристика называется весовой или импульсной переходной функцией и обозначается g(t), т.е. g(t) = y(t) при x(t) = σ (t); при этом:

Обычно при исследовании динамики значения выхода и входа рассматривают не в абсолютных значениях, а в отклонениях от некоторых установившихся значений, т. е. в начальном установившемся режиме x(0) = 0 и у(0) = 0.
Безынерционное звено (усилительное, безъемкостное, масштабирующее или пропорциональное) описывается уравнением:
y(t) = kx(t),
где k — коэффициент пропорциональности или усиления (здесь и во всех последующих уравнениях.
Переходная функция звена (его реакция на единичное ступенчатое воздействие на вход) представлена на рис. 4, а.

 

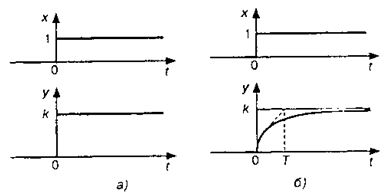
Рис. 4. Реакция безынерционного (а) и инерционного (б) звеньев.

Примеры.
1. Газовая плита: при повороте ручки регулировки расхода газа практически мгновенно устанавливается новая температура пламени.
2. Швейная машина: при повороте ее колеса практически мгновенно иголка займет новое положение.

Инерционное звено (апериодическое, емкостное, релаксационное) описывается дифференциальным уравнением:

При возмущении звена единичным ступенчатым воздействием его переходный процесс описывается уравнением

где Т — постоянная времени, определяемая емкостью звена и его пропускной способностью.

Постоянная времени — это условное время изменения выходной величины от начального значения до нового установившегося значения,, если бы изменение происходило с постоянной.
Скорость изменения функции характеризуется ее производной. Поскольку графически производная в заданной точке определяется как тангенса угла наклона касательной в этой точке, то Т можно определить, проведя касательную к точке наибольшей крутизны кривой разгона от оси времени до асимптоты — установившегося значения выходной переменной у (линии, к которой у стремится). Постоянную времени можно определить и как время, за которое выходная переменная достигнет 63 % своей установившейся величины: при t — Т получаем

Пример
При увеличении затрат на рекламу какого-либо товара новый устойчивый спрос на этот товар устанавливается также с динамическим запаздыванием.

Дифференцирующее звено. Идеальное (безынерционное) дифференцирующее звено опи-сывается дифференциальным уравнением:
y(t) = kx'(t)
Переходная функция звена представлена на рис. 5, а. Во всех точках, кроме нулевой, значение у равно нулю; в нулевой точке у за бесконечно малое время «успевает» увеличиться до бес-конечности и вернуться в ноль. Такого, конечно, в реальной жизни быть не может, поэтому рас-смотрим «реальный» вариант дифференцирующего звена - реальное дифференцирующее звено.

 

Рис. 5. Реакция идеального (безынерционного) звена.

 

Реальное дифференцирующее звено описывается дифференциальным уравнением, в котором, в отличие от реального звена, дополнительно появляется инерционный член Ty'(t):

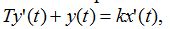
При возмущении звена единичным ступенчатым воздействием переходный процесс в звене описывается уравнением:

Переходная функция звена представлена на рис. 5, б. Реальное дифференцирующее звено не яв-ляется элементарным его можно заменить соединением двух звеньев: идеального дифференцирующего и инерционного:

Пример.
Рассмотрим связь спроса и цены на товар повседневного спроса, например хлеб. При повышении цены на товар в первый же момент произойдет спад спроса на некоторую величину, но в дальнейшем он будет повышаться практически до первоначального уровня.
Интегрирующее звено (астатическое, нейтральное) описывается дифференциальным уравнением
y’(t) = kx(t).

Переходный процесс в звене описывается решением этого уравнения:

при x(t) = l(t) получаем y(t) = kt. Переходная функция звена представлена на рис. 6.

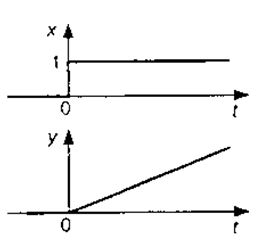
Рис. 6. Реакция интегрирующего звена.

 

Примеры.
1. Изменение уровня в емкости при несбалансированности прихода и расхода жидкости.
2. Изменение количества товара на складе при неравенстве его поступления и отпуска.

Колебательное звено в общем виде описывается следующим уравнением:

Колебательное звено получается при наличии в нем двух емкостных элементов, способных запасать энергию двух видов и взаимно обмениваться этими запасами.

 

Рис. 7. Реакция колебательного звена с затуханием (а) и инерционного звена второго порядка (б).

 

Если в процессе колебаний запас энергии, полученный звеном в начале возмущения, уменьшается, то колебания затухают, т. е. имеем колебательное звено с затуханием (рис. 7, а). При этом (т. е. корни характеристического уравнения - комплексные), и колебательный процесс описывается уравнением:

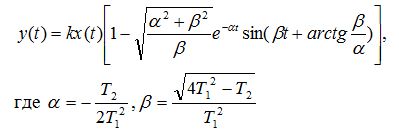
то характеристическое уравнение имеет вещественные корни и вместо колебательного звена получается апериодическое звено второго порядка (рис. 7, б) с переходным процессом

Апериодическое звено второго порядка представляет собой последовательное соединение двух апериодических звеньев первого порядка.

 

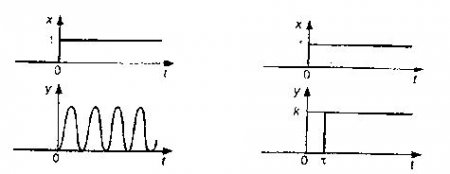
Рис. 8. Реакция консервативного звена. Рис. 9. Реакция звена чистого запаздывания.

 

При Т₂ = 0 получаем консервативное звено с незатухающими колебаниями (рис. 8).

Звено чистого (транспортного) запаздывания повторяет по форме входной сигнал, но с за-паздыванием по времени (рис. 9):
y(t) = kx(t - τ ),
где τ - время запаздывания.

 

Пространство состояний.

Поскольку свойства системы выражаются значениями ее выходов, то состояние системы можно определить как вектор значений выходных переменных Y = (y₁,.., y_m). Выше говорилось (см. вопрос №11), что среди составляющих вектора Y, кроме непосредственно выходных переменных появляются произвольные от них.
Поведение системы (ее процесс) можно изображать разными способами. Например, при m выходных переменных могут быть следующие формы изображения процесса:
o в виде таблицы значений выходных переменных для дискретных моментов времени t₁, t₂…t_k;
o в виде m графиков в координатах y_i - t, i = 1,..., m;
o в виде графика в m-мерной системе координат.
Остановимся на последнем случае. В m-мерной системе координат каждой точке соответст-вует определенное состояние системы.
Множество возможных состояний системы Y (у ∈ Y) рассматривают как пространство состояний (или фазовое пространство) системы, а координаты этого пространства называют фазовыми координатами.
В фазовом пространстве каждый его элемент полностью определяет состояние системы.
Точка, соответствующая текущему состоянию системы, называется фазовой, или изображающей, точкой.
Фазовая траектория — это кривая, которую описывает фазовая точка при изменении состояния невозмущенной системы (при неизменных внешних воздействиях).
Совокупность фазовых траекторий, соответствующих всевозможным начальным условиям, называется фазовым портретом.
Фазовый портрет фиксирует только направление скорости фазовой точки и, следовательно, отражает лишь качественную картину динамики.

Построить и наглядно представить фазовый портрет можно только на плоскости, т. е. когда фазовое пространство является двухмерным. Поэтому метод фазового пространства, который в случае двухмерного фазового пространства называется методом фазовой плоскости, эффективно используется для исследования систем второго порядка.
Фазовой плоскостью называется координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы.
Неподвижными (особыми или стационарными) называются точки, положение которых на фазовом портрете с течением времени не изменятся. Особые точки отражают положения равно-весия.

Использование фазовой плоскости вполне оправдано, поскольку состояние системы как минимум определяется двумя переменными: значением выходной координаты системы и скоростью ее изменения. В дальнейшем будем считать, что на оси абсцисс фазовой плоскости откладываются зна-чения выходной координаты y₁ = y, а на оси ординат - скорость ее изменения y₂ = y' (рис. 1).

 

Рис. 1. Пример фазового портрета.

Тогда для фазовых траекторий невозмущенной системы справедливы следующие свойства:
o через одну точку фазовой плоскости проходит только одна траектория;
o в верхней полуплоскости изображающая точка движется слева направо, а в нижней - соот-ветственно наоборот;
o на оси абсцисс производная dy₂/dy₁ = ∞ всюду, за исключением точек равновесия, поэтому фазовые траектории пересекают ось абсцисс (в неособых точках) под прямым углом.
Линейная система имеет единственную особую точку - начало координат. Нелинейные си-стемы характеризуются большим разнообразием фазовых портретов - они могут иметь несколько особых точек.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: