Системный подход к прогнозированию.

Слово «прогноз» происходит от греческого слова «prognosis» (предвидение, предсказание о развитии чего-либо, основанное на определенных данных). Прогнозирование широко используется во многих областях человеческой деятельности, особенно актуально прогнозирование в задачах управления.
Процесс разработки прогнозов называется прогнозированием.
Под методами прогнозирования подразумевают совокупность приемов мышления, способов, позволяющих на основе анализа информации о прогнозном объекте вынести относительно достоверное суждение о его будущем развитии. Тип применяемого метода зависит от типа объекта. Существует большое количество классификаций видов прогнозов по различным классификационным признакам.

1. Постановка задачи прогнозирования.
Прогнозирование означает предсказание состояния какого-либо объекта, процесса или явления в будущем. Фактически любое моделирование дает прогноз, т. е. отвечает на вопрос: «Что будет если...? », но здесь мы ограничимся прогнозированием в более узком смысле. Различают такие виды прогнозов, как прогноз погоды, предсказание хода болезни, научно-технический прогноз, прогноз экономический и т. д. В данной книге мы будем в основном говорить об экономическом прогнозе, который тесно связано с планированием и управлением.
Задачу прогнозирования в самом общем виде можно поставить следующим образом. Имеется некоторый прогнозируемый показатель Р. Необходимо определить значение P_s этого показателя в некоторый заданный момент времени в будущем s.
По времени упреждения прогнозирование разделяется на текущее, краткосрочное, среднесрочное, долгосрочное и сверхдолгосрочное. В зависимости от характера и цели прогнозирования диапазон каждого из видов прогноза может простираться от долей секунды (например, в физике) до миллиардов лет (в космологии). В экономических и общественных науках рассматривают прогнозы: краткосрочные (1-2 года), среднесрочные (5-10 лет), долгосрочные (15-20 лет) и сверхдолгосрочные (30-100 лет). Существуют и другие классификации по срокам прогноза.
Наиболее распространен такой подход к прогнозированию. Анализируется временной ряд значений прогнозируемого показателя, устанавливается закономерность изменения показателя во времени, а затем эта закономерность экстраполируется на будущие моменты времени. Однако такой подход не всегда дает удовлетворительный прогноз, поскольку основан на учете только части причин, по которым происходит изменение прогнозируемого показателя. Для повышения точности прогноза необходимо провести системный анализ: определить факторы, действующие в объекте исследования, и оценить их влияние на прогнозируемый показатель. На основании результатов анализа можно выбирать методы прогнозирования, в наибольшей степени пригодные для решения конкретной задачи.
Основу прогнозирования составляют либо причинно-следственные связи между прогнозируемым показателем и факторами, на него влияющими, либо инерционные свойства объекта (в этом случае «причиной» является время).
Основой любого прогнозирования является гипотеза об инерционности объекта. Причем инерционность можно рассматривать не только временную (в последующие моменты времени прогнозируемый показатель будет изменяться в том же направлении, что и сейчас), но и более широко — инерционность функциональную. В этом случае функциональная зависимость прогнозируемого показателя от факторов, на него влияющих (в частном случае это может быть и время), известная на некотором интервале изменения этих факторов, продолжается и за пределами интервала.
Примеры:
1. Последние несколько дней температура воздуха падала ежедневно на 1 °С. Можно предположить, что эта тенденция сохранится и ближайшие дни.
2. Цепа на сахар последние месяцы росла в среднем на 3 %. Можно прогнозировать сохранение этой тенденции и в последующие месяцы.
3. Пусть зависимость спроса на некоторый товар Сп от его цены Ц при изменении цены от 10 до 14 р. описывается моделью вида:

Можно предполагать, что при ценах, меньших 10 р. или больших 14 р., эта зависимость сохранится.
На инерционности построен метод научного исследования - экстраполяция (от лат. extra сверх и polio - приглаживаю, выправляю).
Экстраполяция - это распространение результатов, полученных из наблюдений над одной частью явления, на другую его часть.
Экстраполяция закономерностей - это перенос закономерностей, выявленных на одном материале и одном классе задач, на другой материал и другой класс задач.
С математической точки зрения:
Экстраполяция - это приближенное определение значений функции F(x) в точках х, лежащих вне отрезка [х₀, х_n], по ее значениями в точках х₀ < х₁ < ... < х_n.

2. Причины изменения прогнозируемого показателя.
Если ставится задача прогнозирования значения некоторого показателя, то закономерно возникает вопрос о причинах его изменения. Такие причины можно разбить на две группы: внешние причины (по отношению к исследуемой системе) и внутренние.
К внешним причинам относятся изменения: возмущающих переменных - вектор Х; управляющих переменных - вектор U; неконтролируемых переменных (шумов или помех) — вектор ε.
К внутренним причинам относятся такие свойства объекта, как динамичность (инерционность), нестационарность, целенаправленность (активность).
Рассмотрим влияние на прогнозируемый показатель каждой из причин в отдельности.

2.1. Влияние возмущающих и управляющих переменных
Если пренебречь остальными причинами, то влияние возмущающих и управляющих переменных (для простоты обозначим их векторы пока одной буквой Х) можно представить в виде следующей математической модели:
Р = F(X) (1)
Зная функцию F и значение входной перемен X_s в заданный момент времени в будущем s, можно вычислить значение прогнозируемого показателя P_s:
P_s = F(Х_s).

2.2. Влияние неконтролируемых переменных
Если мы знаем, что ни возмущающие, ни управляющие переменные не изменятся к моменту времени s, а единственной причиной изменения Р являются шумы ε, то надо рассматривать такую модель:
P=F(ε ) (2)
К сожалению, в этом случае мы чаще всего не знаем причин и значений неконтролируемой переменной ε. Поэтому построение соответствующей математической модели типа (2) является проблематичным. Единственное, что можно сказать, так это то, что при нулевом среднем значении ε значение прогнозируемой переменной в среднем не изменится.

2.3. Влияние динамичности
Динамические системы, как правило, являются инерционными, т. е. даже при отсутствии наблюдаемых изменений входных переменных выходная переменная продолжает изменяться. Единственный «виновник» этого - время, т. е. если бы удалось остановить время, то выходная величина перестала бы изменяться.
Таким образом, если мы работаем с данными, относящимися к некоторому периоду времени, в пределах которого входные переменные можно считать неизменными, поведение прогнозируемого показателя можно описывать моделью
P(t) = F(t) (3)
Это характерно для систем, содержащих инерционные, интегрирующие, реальные дифференцирующие и колебательные звенья.

2.4. Влияние нестационарности
В нестационарной системе происходит изменение ее структуры и/или параметров. В модели (1) прогнозируемый показатель зависит не только от входных переменных, но и от вектора параметров (коэффициентов) А. Тогда более точное представление модели (1) будет следующим:
P = F(X, A) (4)
Если система стационарная, то при изменении входных воздействий модель (4) можно записать
P(t) = F(X(t), A).
Для нестационарной системы при неизменных внешних воздействиях на объект модель будет иметь вид:
P(t) = F(X, A(t)) (5)
Или
P(t) = F(A(t)) (5’)
В этом случае задача прогнозирования показателя Р столкнется с проблемой прогнозирования значения параметров А. Если она будет решена успешно (что чаще всего невозможно) и будет построена модель (5'), то можно надеяться и на решение основной задачи. Изменение парамет-ров может быть монотонным, случайным или управляемым. В первом случае параметры являются функциями времени А(t), что соответствует рассмотренной выше задаче построения динамической модели типа (3). Во втором - параметры изменяются случайным образом. Это можно рассматривать как влияние неконтролируемых переменных - модель типа (2).
При управляемом изменении параметров объект не является нестационарным и может описываться моделью типа (4).

2.5. Влияние целенаправленности (активности)
К целенаправленным объектам относятся объекты, элементам которых являются люди. В таких объектах каждый отдельный человек или группа людей способны поставить свои цели и действовать в соответствии с ними. В этом случае следует говорить о том, что структура зависимостей типа (1), (3) или (4) уже сама будет изменяться во времени, даже при неизменных Х, А или ε:
P(t)=F_t(· ).
Формальные методы прогнозирования здесь малопригодны - это поле деятельности в основном для психологов.

3. Выбор метода прогнозирования.
Всего известно около двухсот методов прогнозирования, которые базируются на трех ос-новных подходах (классах методов):
1) экстраполяционный, когда единственной причиной изменения прогнозируемого показателя считается время (используется инерционность процессов во времени);
2) модельный, при котором ищется функциональная зависимость прогнозируемого показателя от факторов, на него влияющих;
3) экспертный - прогноз на основании мнений экспертов.

3.1 Экстраполяционный подход к прогнозированию.
Этот подход заключается в установлении закономерности изменения прогнозируемого показателя за предыдущие моменты времени с последующей экстраполяцией этой закономерности на последующие моменты времени. При экстраполяционном подходе единственной причиной изменения прогнозируемого показателя считается время. Для определения закономерности изменения прогнозируемого показателя Р во времени (другими словами, модели Р = F(t)) необходимо знать значения прогнозируемого показателя в предыдущие моменты времени. Прогнозирование в этом случае заключается в установлении закономерности изменения прогнозируемого показателя за предыдущие моменты времени с последующей экстраполяцией этой закономерности на следующие моменты времени. Таким образом, этот подход пригоден только для прогнозирования динамических процессов. Из-за простоты и наглядности это самый распространенный подход при количественном прогнозировании в экономике, которая по своей сути представляет собой совокупность динамических процессов.
Тенденции развития экономических показателей. Статистическое описание движения экономических явлений осуществляется с помощью динамических (временных) рядов. Поведе-ние динамического ряда, характеризующего развитие экономического явления, традиционно рассматривают как сумму четырех компонент, которые непосредственно не могут быть измерены (ненаблюдаемые компоненты): вековой уровень (или тренд), циклическая составляющая, сезонная составляющая и случайные колебания.
При анализе динамических рядов наибольший интерес вызывает тенденция развития изучаемой системы. Понятие тенденции развития не имеет достаточно четкого определения - под ней понимают некоторое общее направление развития, долговременную эволюцию. Обычно тенденцию развития стремятся представить в виде более или менее гладкой траектории, ко-торую можно формализовать в виде некоторой функции от времени. Такую функцию называют трендом, он описывает фактическую, усредненную для периода наблюдения тенденцию изучаемого процесса во времени.
Наиболее распространенным и простым путем выявления тренда является сглаживание, в частности, скользящим средним. К недостатку скользящих средних можно отнести то, что зачастую они сглаживают (читай, уничтожают) важные мелкие волны и изгибы в тренде!
Изобразив в осях координат «прогнозируемый показатель - время» временной ряд значений Р, после сглаживания можно графически решить задачу прогнозирования путем продолжения вы-явленной тенденции развития для последующих моментов времени.
Кривые роста. Графическое решение задачи прогнозирование является приближенным и носит субъективный характер. Более точный прогноз можно получить с помощью аналитического выравнивания динамических рядов — нахождения модели Р = F(t). При построении этой модели возникают те же проблемы, что и при построении любой другой: выбор структуры модели, оценивание ее параметров (коэффициентов) и оценка точности модели. Рассмотрим первую проблему. При выборе структуры модели проходится определять, какие входные пере-менные войдут в модель и в каком виде. Здесь мы имеем только одну входную переменную t, поэтому задача сужается до поиска функции одной переменной.
Функции, описывающие закономерности развития явления во времени, полученные путем аналитического выравнивания динамических рядов, получили название кривые роста. Вопрос о выборе типа кривой является основным; ошибка этого этапа более значима по своим последствиям, чем ошибка в оценивании параметров. Многолетние исследования временных рядов в экономике, социологии, политике, демографии и других экономико-общественных науках позволили выявить ряд наиболее распространенных кривых роста, описывающих соответствующие явления в этих науках.
Наиболее часто применяют такие простые функции, как:
1) многочлены (полиномы);
2) различного рода экспоненты;
3) логистические кривые.
Многочлены. Для выравнивания временных рядов используются многочлены:
o первой степени: p_t = а₀ +а₁t,
o второй степени: p_t = а₀ +а₁t+а₂t²,
o n-й степени: p_t = а₀ +а₁t+а₂t²+...+а_ntⁿ.
При этом коэффициент a1 можно трактовать как скорость роста, а₂ - ускорение роста, а₃ - изменение ускорения роста. Многочлены первой степени предполагают постоянство приращения ординат для процессов, равномерно развивающихся во времени. Парабола второй степени описывает движение с равномерным изменением прироста, т. е. равноускоренных процессов.
Обоснованием применения полиномов при выборе структуры модели может быть теорема Вейерштрасса, из которой следует, что любую непрерывную функцию на заданном отрезке можно сколь угодно точно описать многочленом.
Экспоненты. Самая простая экспоненциальная (показательная) кривая имеет вид P_t = AB¹. Если это уравнение прологарифмировать, то в полулогарифмических координатах получим уравнение прямой
logP = log a + tlog b.
Более сложную зависимость можно описать логарифмической параболой

 

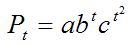
Рассмотренные выше кривые, соответствующие многочленам, не имеют асимптот, их рост ничем не ограничен. В отличие от них экспоненциальная кривая и логарифмическая пара-бола имеют асимптоты, но только в области P_T = 0. Однако есть много процессов, имеющих асимптоту, отличающуюся от нуля. Наиболее простым представителем семейства кривых, имеющих такую асимптоту, является кривая, получившая в статистике название модифицированной экспоненты:

 

Кривая Гомперца и логистическая кривая. В страховых и некоторых демографических расчетах нашла себе применение S-образная кривая, получившая название кривой Гомперца:

 

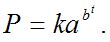
Также для описания S-образных кривых применяется логистическая кривая:

 

Экспоненциальные кривые роста хорошо описывают процессы, имеющие так называемый лавинообразный характер, а именно, когда прирост зависит в основном от уже достигнутого уровня.
Если же на процесс все время воздействует ограничивающий фактор, то хорошее описание этого процесса можно получить с помощью модифицированной экспоненты. Если же ограничивающий фактор начинает влиять только после некоторого момента времени (точка перегиба), то наилучшее приближение дают S-образные кривые, которые описывают два встречных лавинообразных процессам один с ускорением развития, другой - с замедлением.

3.2. Модельный подход к прогнозированию
Рассматривая задачу прогнозирования, мы предполагали, что прогнозируемая величина является функцией времени. Однако, часто это слишком упрощенный подход. Конечно, например, радиоактивный распад можно считать зависимым только от времени, но большинство прогнозируемых показателей все же зависит от других факторов. Например, прогнозирование числа больных в данном населенном пункте зависит не от времени как такового, а от числа жителей, экологической обстановки и т.п. И если в следующем году число жителей резко сократится или возрастет, то во столько же раз изменится потенциальное число больных.
При модельном подходе ищется функциональная зависимость прогнозируемого показателя от факторов, на него влияющих. Модельный подход потенциально дает самый точный прогноз, но является наиболее сложным и наукоемким.
Вернемся к причинам изменения прогнозируемого показателя и оценим пригодность тех или иных подходов к прогнозированию.
1. Если изменение прогнозируемого показателя связано только с динамическими процессами (а точнее, процесс изменения Р(t) является частью переходного процесса), то наиболее эффектив-ным будет применение экстраполяциопного подхода.
При этом причинами изменения Р могут быть:
o переходные процессы, происходящие в объекте; динамические процессы в объекте, приводящие к изменению его параметров A(t) (можно рассматривать и динамические процессы в психике людей, входящих в качестве элементов исследуемого объекта);
o динамические процессы, протекающие вне объекта, следствием чего могут быть изменения возмущающих и неконтролируемые переменных - Х(t) и ε (t).
В общем виде это можно описать такой моделью:
P(t) = F(X(t), A(t), ε (t), t) (6)
При этом, если мы не можем построить модель типа (6), прогнозная модель будет строиться на основании временных рядов и описывать зависимость прогнозируемого показателя только как функцию времени.
2. Другим подходом к прогнозированию динамических процессов можно назвать модельный авторегрессионный подход, когда строится модель, связывающая значения прогнозируемого показателя в некоторый момент времени s со значениями этого же показателя в предыдущие моменты времени:
P(s) =F[P(s-l), P(s-2),...].
Авторегрессионная модель является попыткой описать динамический процесс алгебраическим уравнением вместо дифференциального.
3. Если изменение прогнозируемого показателя нельзя объяснить только как функцию времени (т. е. объяснить только динамическими процессами), то применяется модельный подход, при котором в модели учитываются возмущающие и управляющие переменные.
Такой подход предполагает, что прогнозируемая величина является выходной переменной исследуемого объекта (процесса или явления) Р = у и, в первую очередь, зависит от множества различных повременных факторов Х = {х₁,..., х_n}.
Строятся как простейшие модели типа (1) так и более сложные, учитывающие запаздывающие переменные и время:
P(t) = F[X(t), X(t-l), X(t-2),.., t],
а также авторегрессионные составляющие:
P(t) = F[Р(t-1), P(t-2),..., X(t), X(t-1), X(t-2),..., t].
Построение таких моделей связано с серьезными трудностями. Хотя следует сказать, что такая полная модель никогда и не используется для прогнозирования, но всегда можно допускать присутствие ее членов в прогностической модели. Здесь мы сталкиваемся с серьезной задачей выбора структуры модели, а именно, отбора значимых членов модели. Во-первых, довольно сложно выбрать структуру модели; второй проблемой является ограниченное количество экспериментальных данных, что не позволяет получить статистически значимые оценки параметров модели.

3.3. Оценивание точности прогнозных моделей
В предыдущем разделе рассматривался вопрос выбора структуры прогнозных моделей. Что касается оценивания параметров этих моделей, то здесь нет никаких отличий от традиционной задачи построения моделей, и обычно применяется метод наименьших квадратов.
Особую проблему представляет вопрос оценки качества прогнозной модели. Выше говорилось, что критерий качества модели должен определяться той целью, для которой строится модель. Прогнозная модель строится с целью предсказания значения выходной переменной в будущие моменты времени, т. е. нам надо проверить, правильно ли модель предсказывает. Но если мы предсказываем либо на год или больше вперед, то только через этот срок сможем узнать, хороша ли наша модель. Это, безусловно, нас не устраивает. Остается единственный выход — «спрятать» одно или несколько (k) последних по времени известных значений прогнозируемой величины, построить прогнозную модель по оставшимся значениям и попытаться спрогнозировать известные значения (р_i^m, i= 1,..., k). Из множества прогнозных моделей лучшей будем считать ту, которая имеет минимальное значение следующего критерия:

 

Вообще же точность прогноза определяют несколько факторов.
1. Объем статистики (длина предыстории) - чем данных больше, тем надежнее прогноз. Это верно, к сожалению, только с позиций математической статистики - «чем больше, тем лучше». При прогнозировании социально-экономических и политических процессов часто имеют дело с резкими изломами тенденций изменения прогнозируемых показателей. В этом случае в выборке могут присутствовать разные тенденции. Обработка таких данных приведет к получению некой усредненной тенденции («средней температуре по больнице»), по которой можно получить «среднее» значение прогнозируемого показателя.
2. Неизменность тенденции изменения прогнозируемого показателя - важно, чтобы в вы-борке данных для прогнозирования присутствовали только данные, относящиеся к текущей тенденции. Иногда таких данных бывает крайне мало, что не позволяет сделать надежный прогноз.
3. Глубина (интервал) прогноза - чем он больше, тем сильнее возрастает ошибка прогноза. Есть эмпирическое правило - длина предыстории должна как минимум втрое превышать интервал прогноза.
Пример. Пусть нам необходимо спрогнозировать цену на хлеб в следующем месяце. Можно взять ряд данных о цене на хлеб за прошедшие 100 лет, Умножив на 12 месяцев, получаем 1200 «точек» для построения прогнозных моделей. Эта огромная выборка даст нам усредненную тенденцию за сто лет, которая с крайне малой вероятностью будет соответствовать тенденции изменения цены на хлеб «завтра». Если же мы возьмем выборку, отражающую тенденцию последних месяцев, и экстраполируем полученную тенденцию на сто лет вперед, то достоверность такого прогноза тоже будет чрезвычайно низкой, поскольку очень мала вероятность сохранения современной тенденции изменения цены на хлеб.

3.4. Экспертный подход
Экспертный подход основывается на экспертных оценках специалистов в своей области.
Экспертные оценки - это неформальный прогноз, основанный на опыте и интуиции специалистов-экспертов.
Такой прогноз обычно применяют в тех случаях, когда либо прогнозируемый показатель и/или факторы, на него влияющие, измеряются в качественных шкалах, либо но ним отсутствует репрезентативная (достаточная) статистика. Экспертные оценки вытекают из анализа и обобщения процессов, происходивших в прошлом и происходящих и настоящем.
Сущность экспертных методов прогнозирования заключается в построении рациональной процедуры интуитивно-логического мышления человека в сочетании с количественными методами оценки и обработки полученных результатов.
Метод экспертных оценок базируется на предположении, что на основе мнений экспертов возможно построить адекватную модель будущего развития системы. Исходной информацией при этом служат мнения специалистов, занимающихся исследованиями и разработками в прогнозируемой области. Экспертные оценки разделяют на индивидуальные и коллективные в зависимости от того, разрабатывается ли прогноз на основе суждений одного эксперта или группы их.
Индивидуальные экспертные оценки бывают двух типов: оценки типа «интервью» и аналитические. Оценка типа «интервью» это беседа прогнозиста с экспертом, в ходе которой прогнозист, в соответствии с заранее разработанной программой, ставит перед экспертом вопросы относительно перспектив развития прогнозируемого объекта. Процесс аналитической экспертной оценки заключается в самостоятельной работе эксперта, направленной на анализ тенденций и оценку будущего состояния и путей развития прогнозируемого объекта.
Применение коллективных экспертных оценок позволяет повысить точность прогноза. Методы коллективных экспертных оценок разделяются на метод комиссий, метод отнесенной оценки и дельфийский метод.
Метод комиссий - это проведение группой экспертов дискуссии с целью выработки общей по-зиции по вопросам будущего развития прогнозируемого объекта. Недостатком этого метода является взаимное влияние экспертов, экспертам часто бывает трудно отказаться от публично высказанного мнения.
Частично эту проблему решает метод отнесенной оценки (метод «мозгового штурма»), при котором эксперты сначала высказывают любые оценки без права их критики другими и только потом анализируют эти оценки и по ним делают выводы. При этом в качестве экспертов могут привлекаться не только специалисты по данной проблеме, но и специалисты в других областях.
Дальнейшим развитием методов коллективной экспертной оценки является дельфийский метод (по названию древнегреческого города Дельфы). Этот метод предполагает отказ от прямых коллективных суждений. Дебаты заменяются индивидуальными опросами в форме заполнения таблиц экспертной оценки. Ответы экспертов обобщают и вместе с новой дополнительной информацией и обобщенными аргументами передают в распоряжение экспертов, после чего они уточняют свои первоначальные ответы. Такая процедура повторяется несколько раз до достижения приемлемой сходимости высказанных мнений.
Дельфийский метод дает надежные прогнозы на период 1—3 года и более отдаленный период. В зависимости от цели прогноза привлекают от 10 до 100 экспертов.
Достоинством экспертных методов является их относительная простота и применимость для прогнозирования практически любых ситуаций, в том числе и в условиях неполной информации, а недостатком - субъективизм экспертов и невысокая точность прогноза опять же в условиях неполной информации («из ничего нельзя получить ничего»).

Резюме
1. Процесс разработки прогнозов называется прогнозированием. Прогнозирование означает предсказание состояния какого-либо объекта, процесса или явления в будущем. Фактически любое моделирование дает прогноз, т. е. отвечает на вопрос: «Что будет, если...? "
2. По времени упреждения прогнозирование разделяется на текущее, краткосрочное, среднесрочное, долгосрочное и сверхдолгосрочное. В зависимости от характера и цели прогнозирования диапазон каждого из видов прогноза может простираться от долей секунды (например, в физике) до миллиардов лет (в космологии).
3. Основой любого прогнозирования является гипотеза об инерционности объекта. Причем инерционность можно рассматривать не только временную, но и более широко - инерционность функциональную, когда функциональная зависимость прогнозируемого показателя от факторов, на него влияющих, известная на некотором интервале изменения этих факторов, продолжается и за пределами интервала. На инерционности построен метод научного исследования - экстраполяция - распространение результатов, полученных из наблюдений над одной частью явления, на другую его часть.
4. Причины изменения прогнозируемого показателя можно разбить на две группы: внешние причины (возмущения, управление и помехи) и внутренние (нестационарность, ак-тивность и динамичность).
5. Можно выделить следующие основные подходы к прогнозированию: экстраполяционный (единственной причиной изменения прогнозируемого показателя считается время), модельный (ищется функциональная зависимость прогнозируемого показателя от факто-ров, на него влияющих) и экспертный (прогноз на основании мнений экспертов).
6. Одной из проблем прогнозирования является вопрос оценки качества прогнозной модели.
7. Важной проблемой построения прогнозных моделей является ограниченность количества данных предыстории (длина предыстории должна как минимум втрое превышать интервал прогноза), что затрудняет применение таких моделей в условиях частой смены тенденций изменения системы.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: