Принцип возможных перемещений и общее уравнение динамики.

Принцип возможных перемещений.

Эффект связей можно учитывать не только вводя их реакции, но и рассматривая те перемещения, которые точки механической системы могут иметь при наложенных на нее связях. Такой метод позволяет сразу получить уравнение равновесия или движения системы, не содержащие наперед неизвестных реакций связей, что существенно облегчает решение многих задач механики. Эти перемещения называют возможными или виртуальными перемещениями. Они должны быть малыми (элементарными), так как при конечном перемещении система может прийти в положение, где эффект наложенных связей будет другим; быть такими, чтобы все наложенные в данный момент времени на систему связи сохранились, иначе может измениться вид рассматриваемой механической системы.

Следует различать действительное элементарное перемещение от виртуальных перемещений. Поэтому возможное перемещение принято обозначать , при этом δ s будет обозначать его модуль , а - проекции на координатные оси.

Следует отметить также, что число независимых между собой возможных перемещений системы равно ее числу степеней свободы.

Обозначим равнодействующие всех(внешних и внутренних) активных сил и реакции связей действующих на некоторую точку системы соответственно через и . В случае равновесия механической системы, когда каждая ее точка находится в равновесии, имеет место равенство

Умножаем это равенство скалярно на и получим

Сложив эти равенства по индексу k получим

В случае идеальных связей сумма работ их реакций на любом возможном перемещений равна нулю, т.е. . Тогда окончательно приходим к соотношению

(4.54)

которое характеризует принцип возможных перемещений: для равновесия механической системы с иральными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Уравнение (4.54) можно записать в аналитической форме

(4.55)

Равенства (4.54) и (4.55) часто называют общим уравнением статики.

Принцип Даламбера – Лагранжа

Принцип возможных перемещений дает общий метод решения задач статики, а принцип Даламбера позволяет использовать методы статики для решения задач динамики. Следовательно, применяя эти два принципа одновременно мы можем получить общий метод решения задачи динамики. Согласно принципу Даламбера система активных сил , реакций связей и сил инерции образуют уравновешенную систему сил. Тогда, применяя к этим силам принцип возможных перемещений, получим

Но поскольку связи идеальные и , окончательно запишем

(4.56)

Равенство (4.56) выражает принцип Даламбера – Лагранжа, при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещений системы будет равна нулю. В аналитической форме уравнение (4.56) имеет вид

(4.57)

Уравнение (4.56) и (4.57) называют общим уравнением динамики.

Задача Д5

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока (рис. Д5.0 – Д5.9, табл. Д5). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: а шкива 2 их радиусы инерции относительно осей вращения равны соответственно и

Пренебрегая трением, определить ускорение груза, имеющего большой вес; веса шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).

Указания. Задача Д5 – на применение к изучению движения системы общего уравнения динамики (принципа Даламбера – Лагранжа). Предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом где - момент инерции тела относительно оси вращения, - угловое ускорение тела; направление противоположно направлению .

Таблица Д5

Номер условия

Рис. Д5.0

Рис. Д5.1

Рис. Д5.2

Рис. Д5.3

Рис. Д5.4

Рис. Д5.5

Рис. Д5.6

Рис. Д5.7

Рис. Д5.8

Рис. Д5.9

Пример Д5. Механическая система (рис. Д5) состоит из обмотанных нитями блока1 радиуса R1 и ступенчатого шкива 2 (радиусы и , радиус инерции относительно оси вращения ), а также из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к блоку 1.

Дано:

Определить: ускорение груза 3, пренебрегая трением.

Рис. Д5

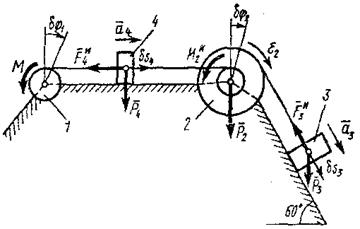
Решение. 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, - идеальные.

Для определения применим общее уравнение динамики:

(1)

Где - сумма элементарных работ активных сил; - сумма элементарных работ сил инерции.

2. Изображаем на чертеже активные силы и пару сил с моментом М. Задавшись направлением ускорения , изображаем на чертеже силы инерции и пару сил инерции с моментом величины которых равны: