За одно и то же время теплоход прошел 216 км, а пароход 72 км. Найти скорость теплохода, если скорость парохода 24 км в час.

I. Этап восприятия и осмысления текста задачи.
Цели:
– понять в целом ситуацию, описанную в задаче;
– выделить условия и требования;
– назвать известные и искомые объекты;
– выделить все отношения (зависимости) между объектами.

Приём выполнения	Образец рассуждения
1.Получение информации о содержании задачи Формы получения информации: – чтение про себя; – чтение вслух; – слушание текста задачи. Обратить внимание на – правильное прочтение слов и предложений; – расстановку логических ударений и ударных слогов.	За одно и то же время теплоход прошел 216 километров, а пароход 72 километра. Найти скорость теплохода, если скорость парохода 24 километра в час.
2.Представление ситуацииСодержание работы: описание ситуации, данной в задаче. Формы представления: – словесное моделирование; – зрительное представление.	Нам известно, что по воде движутся теплоход и пароход.Теплоход движется быстрее, потому что за одно и то же время он прошёл большее расстояние.
3.Переформулирование текста задачи: Вид переформулировки: перенос части условия из требования.	Нам известно, что за одно и то же время теплоход прошёл 216 км, а пароход 72 км со скоростью 24 км/ч. Надо найти скорость теплохода.
4.Определение вида задачи. Выделение величин, данных в задаче	Задача на движениедвух тел. Тройка величин: – скорость(v=s: t) – время(t=s: v) – расстояние(s=v )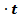
5.Деление задачи на смысловые части по утверждениям	теплоход прошёл 216 км, пароход прошел 72 км. Теплоход и пароход двигались одно и то же время, скорость парохода 24 км/ч. Надо найти скорость теплохода,
6.Уточнение: является ли текст задачей? Примечание. Выявление признаков задачи: – наличие условия, требования; – связь условия с требованием.	В данном тексте есть условие и требование.
7.Беседа на понимание текста задачи Осмыслениехарактеристик задачи – О чем говорится в задаче? – О каких объектах идет речь? – Какие количественные характеристики известны в задаче? – Каково требование в задаче?	– О движении двух объектов. – О теплоходе и пароходе. – 216 км – расстояние, пройденное теплоходом; 72 км – расстояние, пройденное пароходом; 24 км/ч – скорость парохода. – Найти скорость теплохода.
8.Построение вспомогательной модели Вид модели: схематический рисунок. Соотнесение величин с языком схемы: – верхняя, маленькая дуга (мерка)– скорость; – количество таких дуг (мерок) – время; – нижняя дуга (целое) расстояние.	Соотнесение величин с языком схемы: 1)? км/ч; 24км/ч(верхние дуги) – скорость; ? ч – время; 72км, 216км – расстояние. 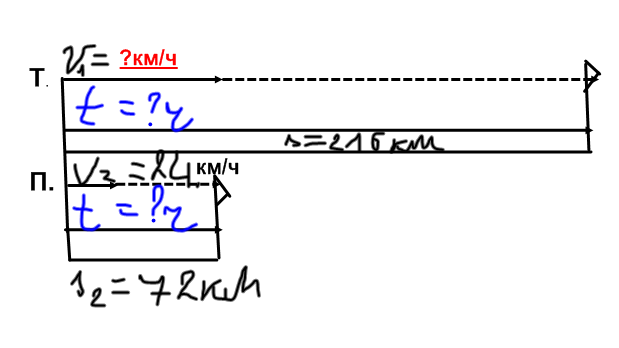1-я часть схемы поясняет характеристики теплохода; 2-я часть – поясняет характеристики парохода.
9.Построение вспомогательной модели Вид модели: таблица. На модели указать: – все объекты; – величины; – количественные характеристики; – требования.	Объект скорость время расстояние Теплоход ? км/ч Одинаковое (? ч) 72км Пароход 24км/ч 216км

II. Этап поиска плана решения текстовой задачи.
Цель: установить связь между данными и искомыми объектами, наметить последовательность действий по решению задачи.

Прием выполнения	Образец рассуждения
От требования к даннымРазбор задачи по тексту: обратить внимание на вопрос задачи и установить, что достаточно узнать для ответа на этот вопрос. Для этого нужно обратиться к условию задачи и выяснить, есть ли необходимые данные. Если таких данных нет или известна только одна величина, то установить, что нужно знать, чтобы найти недостающие данные.	– Что нужно знать, чтобы ответить на вопрос задачи? (Чтобы найти скорость теплохода надо расстояние 216км разделить на время.)– Знаем ли мы расстояние, пройденное теплоходом? (Да, 216 км.) – Знаем ли мы время, которое теплоход находился в пути? (Нет, оно неизвестно.)– Что можно использовать в условии задачи для нахождения времени, которое теплоход был в пути? (Можно использовать расстояниеи скорость парохода, так как время, затрачен­ное теплоходом и пароходом, одинаковое.)
От требования к даннымРазбор по вспомогательной модели:	– Что требуется найти в задаче? (скорость теплохода.)– Что для этого нужно знать? (расстояние и время.) – Все ли известно? (Нет, не известно время.)– А что известно о времени? (Оно одинаковое.)– Как узнать время? (расстояние 72км делим на скорость 24км/ч) – А теперь можно ответить на требование задачи? (Да, расстояние 216км разделим на полученное время)
От условия к требованиюРазбор задачи по тексту: – выделить в тексте задачи две данные величины и на основе знания связи между ними определить, какая неизвестная величина может быть найдена по этим данным с помощью арифметического действия; – затем, считая это неизвестное данным, вновь выделить две взаимосвязанные данные величины, определить неизвестную, которая может быть найдена по ним и с помощью какого действия и т.д., пока не будет выяснено, какое действие приводит к получению искомой в задаче величины.	– Что означает число 72? (Путь, пройденный пароходом.)– Что означает число 24? (Скорость парохода.)– Какую величину можно найти, зная расстояние и скорость? (Время движения парохода.)– Если мы узнаем время движения парохода, то что еще мы узнаем? (Время движения теп­лохода).– Что еще известно про теплоход? (Известно, что он прошел 216 км.) – Что требуется найти в задаче? (Надо найти скорость теплохода).– Можем ли мы ответить на вопрос задачи? (Да, мы знаем расстояние, пройденноетеплоходом216км, и время, которое он был в пути.)
От условия к требованию: Разбор по вспомогательной модели:	– Движение какого транспорта характеризует первая часть схемы? (Теплохода.) – Что можно сказать о времени, пройденном теплоходом? (Оно равно времени, пройден­ному пароходом.) – Разъясните ту часть схемы, которая характеризует движение теплохода. (Это первая часть схемы, в ней необходимо найти скорость; известно расстояние и найдено время.) Что известно о движении парохода? (расстояние 72 км.)- Как найти его время? (расстояние 72км разде­лить на скорость 24км/ч; ( 72: 24.) – Что можно сказать о времени, пройденном теплоходом? (Оно равно времени, пройден­ному пароходом.) – Разъясните ту часть схемы, которая характеризует движение теплохода. (Это первая часть схемы, в ней необходимо найти скорость; расстояние, пройденное тепло­ходом, разделим на время, пройденное тепло­ходом, разделим на время.)

III.Этап составления плана решения задачи.
Цель: записать последовательность выполнения действий решения
задачи. Приемы выполнения и образцы
оформления даны в табл. 3.

 

Прием выполнения	Образец оформления
Построение плана решения по вспомогательной модели На языке схемы	1) время = расстояние: скорость. 2) скорость = расстояние: время
Построение плана решения по вспомогательной модели На основе взаимосвязи тройки величин	1) Время = расстояние: скорость. 2) Скорость = расстояние: время.
Составление программы действий Примечание. Промежуточные результаты арифметических действий не находят, записывают условным знаком.	1) 72: 24 = ▲ (ч) 2) 216: ▲ =? (км/ч)
Запись шагов решения в виде выражения Примечание. 1. Запись плана решения осуществляется поэтапно. 2. Фиксируются последовательность действий шагов, затем составляется итоговое выражение.	72: 24 – время, затраченное пароходом; 216: (72: 24) – скорость теплохода.

 

IV.Этап осуществления плана решения задачи.
Цель: найти ответ на требование задачи, выполнив все действия в
соответствии с планом.
Приемы выполнения даны в табл. 4.

 

Прием выполнения	Образец оформления
По действиям с кратким пояснением к каждому выполненному действию Примечание. 1. Равенство записывают в строчку, если прием вычисления устный, в столбик – если прием вычисления письменный. 2. В пояснении слова пишутся полностью. Если слово сокращают, то сокращают после согласной буквы и ставят точку. 3. Точку не ставят при сокращении в том случае, если оно общепринятое. 4. В ответе сначала записывают число, затем его поясняют. 5. В ответе записывают полное пояснение.
По действиям с полным пояснением к каждому выполненному действиюПримечание. 1. Равенство записывают в строчку, если прием вычисления устный, в столбик – если прием вычисления письменный. 2. Найденное значение в каждом арифметическом действии поясняется полностью через черточку после числа. 3. В пояснении допускается общепринятое сокращение. 4. В ответе сначала записывают число, затем его поясняют. 5. В ответе пояснение записывают кратко. (так как нет смысла пояснять одно и то же число дважды).
По действиям с записью вопросов Примечание. 1. Сначала записывают вопросительное предложение, под ним равенство, отвечающее на требование действия. 2. Нумерацию действий записывают перед предложением. 3. Равенство записывают посередине в сравнении с требованием к действию. 4. Равенство записывают в строчку, если прием вычисления устный, в столбик – если прием вычисления письменный. 5. Найденное значение в каждом арифметическом действии не поясняют (исключение: единицы величин, если они не указаны в требовании к выполняемому действию). 6. В пояснении допускается общепринятое сокращение. 7. В ответе сначала записывают число, затем 8. В ответе пояснение записывают кратко.
В виде выражения, преобразуемого после вычислений в равенство, без записи шагов по составлению выраженияПримечание. 1. Равенство записывают посередине. 2. Выражение не должно содержать лишних скобок. 3. Найденное значение в выражении не поясняют (исключение: единицы величин, если они не указаны в требовании к выполняемому действию). 4. В ответе сначала записывают число, затем его поясняют. 5. В ответе пояснение записывают подробно.

 

V. Проверка решения задачи.

Цель этапа - установить правильность или ошибочность выполнения решения.

Известно несколько приемов, помогающих установить, верно ли решена задача.

Рассмотрим основные:

Прикидка

2. Установление соответствия между результатом и условием задачи.

Для этого найденный результат вводится в текст задачи и на основе рассуждений устанавливается, не возникает ли при этом противоречия.

3. Решение задачи другим способом.

Пусть при решении задачи каким-то способом получен некоторый результат. Если её решение другим способом приводит к тому же результату, то задача решена верно.

⇐ Предыдущая123456Следующая ⇒

Поделиться: