Энергетическая характеристика случайного процесса

 

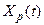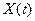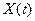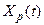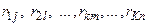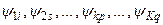Отметим, что каждая отдельная реализация (4.28) входного процесса не отражает в полной мере свойства реального процесса. Все свойства процесса будут выражены только лишь совокупностью реализаций , в которых выборки параметров и соответствуют распределениям случайных величин 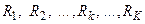и 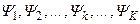. В частности, дисперсия D_x процесса 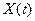не может служить характеристикой средней энергии отдельной реализации 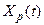. Однако эта дисперсия является характеристикой представительной совокупности реализаций.

Введем в рассмотрение энергетическую характеристику отдельной реализации 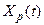. В качестве такой характеристики 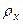можно рассматривать сумму квадратов амплитуд отдельных гармонических составляющих

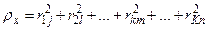. (4.29)

При определенном наборе фиксированных значени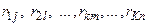й и 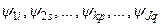, т.е. при заданной реализации входного процесса 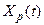соответствующая нелинейная задача динамики (4.1) может быть решена путем численного интегрирования уравнений движения механической системы. При относительно слабо выраженной нестационарности системы (4.1) математические ожидания и дисперсии выходных процессов (вынужденных колебаний) пренебрежимо мало зависят от сдвигов фаз отдельных спектральных составляющих входного процесса, т.е. от факторов 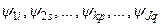. Механические системы, обладающие таким свойством, будем называть квазистационарными. Результаты многочисленных экспериментальных и расчетных исследований показывают, что системы уравнений, описывающие устойчивые режимы качки судна и гидроупругих колебаний его конструкций, являются квазистационарными. При рассмотрении неустойчивых механических систем влияние факторов 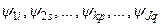на характеристики выходного процесса может быть заметным. В дальнейшем будем считать, что рассматриваемая система устойчива и квазистационарна.

В результате численного решения системы дифференциальных уравнений (4.1) определяется реализация 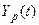выходного процесса 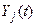. Для этой реализации также может быть вычислена энергетическая характеристика. Процедура вычисления зависит от свойств рассматриваемой механической системы или, точнее, от вида ее реакций на гармонические возмущения, рассмотренных выше в разделе 4.5.

Наиболее просто энергетическая характеристика вычисляется при совпадении числа гармоник и частот входного и выходного процессов. В этом случае вычисления производятся по формуле, аналогичной (4.29)

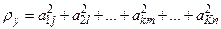. (4.30)

Здесь 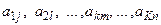- амплитуды гармонических составляющих реализации 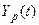выходного процесса, соответствующие частотам .

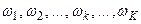При наличии в колебательном решении динамической системы ультрагармонических и субгармонических составляющих по отношению к частотам 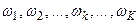, которые могут быть выделены из этого решения, например, с помощью финитного преобразования Фурье, квадрат амплитуды 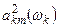определяется следующим образом

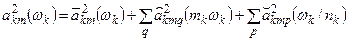, (m_k, n_k = 2, 3, 4, …),

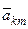- амплитуда основной составляющей выходного процесса; 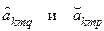- амплитуды ультрагармонических и субгармонических составляющих соответственно.

При хаотическом характере реакции системы на регулярные входные процессы необходимо вычислить дисперсию реализации 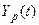и принять энергетическую характеристику 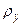равной среднему значению квадрата амплитуды, которое в соответствии с формулой (1.26) в два раза превышает значение дисперсии (в предположении нормальности процесса).

Предположим, что расчет выполнен не только при одной реализации входного процесса вида (4.28), но реализован достаточно объемный численный эксперимент с полнофакторным планом, предусматривавшим фиксирование фактора R_k на N_r уровнях, равных 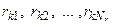, и фактора 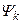на N_y уровнях ( 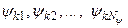). Для каждой реализации входного процесса найдено значение энергетической характеристики 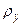реализации выходного процесса. Совокупность этих значений 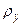представляет собой очень ценную информацию, позволяющую определить вероятностные распределения амплитуд выходного процесса 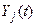. Для оценки таких распределений можно использовать различные методы.

Метод моментов.

При использовании этого метода находят начальные моменты s-го порядка энергетической характеристики 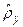как математическое ожидание s-й степени этой случайной величины

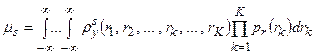. (4.31)

где .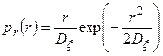

Обычно аналитический вид выражения 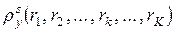неизвестен. Из численного решения системы уравнений (4.1) находят лишь величины 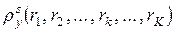, вычисленные при определенных значениях случайных параметров 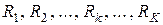(например, при значениях 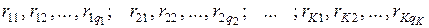, называемых узлами интерполяции). Приближенные значения функции 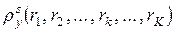в произвольных точках будем определять с помощью интерполяционного полинома Лагранжа

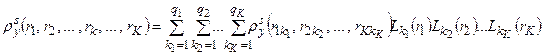, (4.32)

где 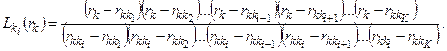(4.33)

Подставив выражение (4.32) в равенство (4.31) и меняя прядок интегрирования и суммирования, получим

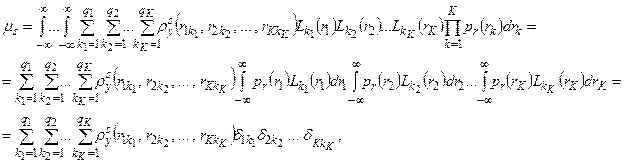где 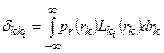- величины, называемые числами Кристоффеля.

Таким образом, для вычисления математического ожидания 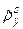в соответствии с формулой (4.31) можно использовать приближенное соотношение

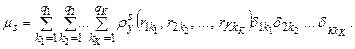(4.34)

Точность приближенной формулы (6.6) определяется рациональным выбором узлов интерполирования .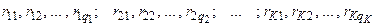

Применение описанного выше интерполяционного метода определения моментов 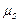теоретически обосновывается на основе теорем, доказательство которых приведено в работе [88]. Мы же здесь ограничимся формулировками этих теорем.

Теорема 1. Если функция 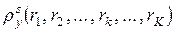, являющаяся решением системы дифференциальных уравнений (4.1), непрерывна по аргументам 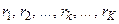за исключением конечного числа точек, где имеются разрывы первого рода, то существует полином относительно 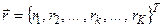, приближающий равномерно в области 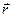Î [a, b] эту функцию с любой наперед заданной точностью за исключением сколь угодно малых окрестностей точек разрыва непрерывности.

Теорема 2. Для того чтобы интерполяционный полином (4.32) сходился слабо в среднем для всякой непрерывной при всех 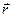Î [a, b] функции 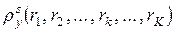, достаточно, чтобы узлы интерполирования были выбраны так, чтобы числа Кристоффеля 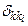были неотрицательны.

Теорема 3. Если в качестве узлов интерполирования выбрать корни ортогональных полиномов по весу, равному 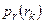- плотности распределения случайной величины 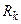, то при использовании n узлов интерполирования интерполяционный метод дает точные значения в классе многочленов 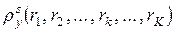всех степеней до степени 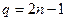включительно.

Теорема 4. Для каждой плотности распределения вероятностей, являющейся весовой функцией, существует единственная система ортогональных многочленов.

Теорема 5. Многочлен H_n(u) степени n, ортогональный относительно плотности распределения вероятностей 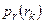, имеет внутри промежутка [a, b] значений, принимаемых случайной величиной 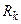, n вещественных корней 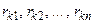(узлов интерполирования). Причем числа Кристоффеля, вычисленные для случая, когда в качестве узлов интерполирования выбраны корни ортогональных многочленов, положительны.

Для некоторых распределений случайных величин (равномерного, экспоненциального, нормального и других) в технической литературе приводятся оптимальные узлы интерполирования и соответствующие им числа Кристоффеля [83, 84, 88]. Для других законов распределения случайных величин узлы интерполирования могут быть вычислены по известным значениям узловых точек для какого-нибудь из указанных выше стандартных распределений, если предварительно установлена функциональная связь между случайными величинами вида

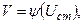
приводящее рассматриваемое распределение вероятностей случайной величины V к распределению стандартной величины .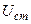

Функция 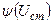определяется из уравнения

,

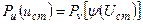где 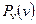- интегральный закон распределения вероятностей случайной величины V; 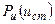- интегральный закон распределения случайной величины 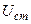, для которой известны узлы типа Чебышева.

Например, если стандартная величина 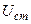имеет показательный закон распределения, для которого

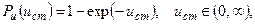
то для отыскания функциональной связи величины 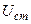со случайной величиной V, распределенной по закону Рэлея

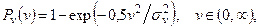
получим уравнение

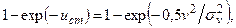
из которого следует, что

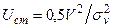(4.35)

или

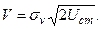(4.36)

Найденное преобразование (4.36) позволяет осуществить переход от закона Рэлея к стандартной форме показательного закона. Таким образом, пересчет узловых точек осуществляется по формуле (4.36), а числа Кристоффеля принимаются при этом одинаковыми.

Найденные таким способом оценки нескольких моментов 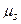приравниваются теоретическим значениям моментов, соответствующим некоторому закону распределения вероятностей величины энергетической характеристики 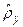, используемому для аппроксимации распределения. Получаемые при этом равенства рассматривают как систему уравнений для определения неизвестных параметров распределения 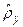. Например, при использовании аппроксимации плотности распределения законом Вейбулла-Гнеденко

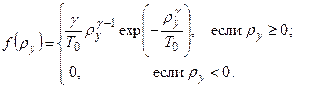(4.37)

эта система уравнений для определения параметров T₀ и g имеет вид

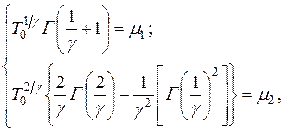
где 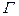- гамма-функция.

 

Располагая известным законом распределения, можно определить плотность распределения амплитуд нелинейных колебаний A_y, используя правило преобразования плотности вероятности случайных величин, связанных функциональной зависимостью 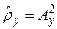. Если плотность распределения случайной величины 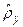задана в форме (4.37), то плотность распределения вероятностей амплитуд колебаний принимает вид:

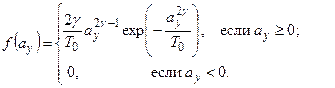
Таким образом, вычисления плотности вероятностей амплитуд выходного процесса системы, заданной уравнениями (4.1), с помощью метода моментов выполняют в следующей последовательности.

1. Определяют рациональную форму аппроксимации по Лагранжу спектральной плотности входного процесса (морского волнения), а также параметры 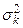математической модели входного процесса (морского волнения) в виде зависимости (4.27).

2. Для заданного порядка интерполяционных многочленов и найденных из таблицы узлов интерполирования для стандартных случайных величин (с пересчетом по формулам вида (4.35) или (4.36)) выбирают значения чисел Кристоффеля, а также значения случайных параметров 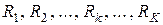, равных 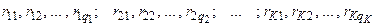, при которых производится интегрирование уравнений (4.1), описывающих поведение рассматриваемой гидроупругой системы.

2. Производят численное интегрирование уравнений системы (4.1) с выбранными значениями случайных параметров, находят периодические решения системы (или хаотические решения, если они существуют в неустойчивых режимах колебаний) и определяют значение функции 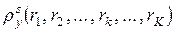в узлах интерполяции.

3. Умножают полученный результат на соответствующие числа Кристоффеля и рассчитывают начальные моменты 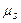энергетической характеристики 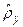по формуле (4.34).

4. Составляют систему уравнений для определения параметров распределения случайной энергетической характеристики 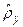, приравнивая найденные моменты 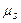их теоретическим значениям, следующим из принятого для аппроксимации закона распределения энергетической характеристики 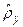. Оценивают параметры распределения случайной величины .

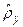5. Находят выражение для плотности распределения вероятностей амплитуд A_y выходного процесса, пользуясь правилом преобразования распределений случайных величин, связанных функциональной зависимостью.

Отметим, что при увеличении числа K случайных параметров 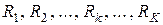оценка распределений амплитуд выходного процесса связана с резким увеличением числа рассматриваемых реализаций входного процесса (нерегулярного волнения), и соответствующих этим реализациям решений системы дифференциальных уравнений (4.1). Происходит также большой рост числа разыскиваемых периодических решений системы при каждом варианте реализации входного процесса. В связи с таким увеличением объема вычислений необходимо ограничивать число K. Обычно его рациональное значение находится в диапазоне от 4 до 6.

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться: