Многоконтурная одномерная САУ

САУ называют многоконтурной, если она помимо главной обратной связи содержит местные обратные или параллельные связи. При наличии обратной связи образуется замкнутый контур передачи воздействия от одного звена к другому.

	Рисунок 12

 

Рассмотрим общий случай одномерной системы, когда она содержит произвольное число связанных друг с другом контуров. Здесь возможны два пути. Первый – это преобразование многоконтурной схемы в эквивалентную одноконтурную, а второй – применение готовых формул для передаточной функции замкнутой системы произвольной сложности.

Рассмотрим первый путь. Для преобразования схемы руководствуются рядом правил: правила замены групп параллельно и последовательно соединенных звеньев, а также звена с обратной связью (мы их рассмотрели в предыдущей главе) и правила переноса воздействий из одной точки системы в другую, которые рассмотрим сейчас.

Эти правила вытекают из условия сохранения неизменными сигналов на выходе системы при выполнении таких преобразований.

f

При перенесении суммирующего элемента вперед по стрелке основного контура в ветвь добавляется фиктивное звено с передаточной функцией 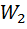обойденного при этом звена основного контура.

 

 

f

При перенесении суммирующего устройства назад добавляется звено с обратной передаточной функцией .

			Рисунок 13

 

В обоих случаях сигнал на выходе рассматриваемой части основного контура сохраняется неизменным. При перенесении точки разветвления правило преобразования обратное: при переносе этой точки вперед в ветвь добавляется звено с обратной передаточной функцией обойденного звена, а при переносе назад – звено с передаточной функцией .

	Рисунок 14

 

Основной задачей преобразования многоконтурной структурной схемы является прежде всего, приведение ее к схеме с неперекрещивающимися связями, когда отдельные контуры схемы не сцепляются друг с другом. После этого каждый из контуров может быть заменен одним эквивалентным звеном с передаточной функцией, определенной по формуле , в результате чего исходная схема приводится к одноконтурной.

Многомерная САУ

Многомерная система, содержащая произвольное число выходных величин m и входных воздействий n описывается передаточными функциями

= , k=1, 2, (22)

Здесь - передаточная функция замкнутой системы, определяющая зависимость k-ой выходной величины от i - ого входного воздействия.

Систему уравнений 22 удобно представить в матрично-векторным уравнением

 

x= - матрица-столбец

f= - матрица-столбец

- матрица размера.

 

Пример поэтапного преобразования

 

УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ.

Основные понятия

Одной из важнейших характеристик АСУ является ее устойчивость.

Устойчивость АСУ – свойство системы возвращаться в состояние равновесия после прекращения изменения воздействия, выведшего систему из этого состояния.

Неустойчивая АСУ не возвращается в состояние равновесия, а непрерывно удаляется от него

От устойчивости АСУ зависит ее работоспособность. Система, не обладающая устойчивостью, вообще не способна выполнять функции управления и имеет нулевую или даже отрицательную эффективность. Неустойчивая система может привести управляемый объект в аварийное состояние. Поэтому проблема устойчивости систем является одной из центральных в теории автоматического управления.

 

Проявлением, по которому можно судить об устойчивости или неустойчивости системы, является характер изменения ее сигналов во времени, например, управляемой величины x(t). Если управляемая величина x(t) после прекращения изменения, например, задающего воздействияx_з(t) становитя с течением времени постоянной (рис.5.1, а), то система ведет себя устойчиво. Если же управляемая величина x(t) – возрастает, то система ведет себя неустойчиво.

Рис. 1. Графики изменения сигналов АСУ во времени

а – устойчивая АСУ; б – неустойчивая АСУ

Причинами неправильного действия главной обратной связи АСУ являются:

• Выполнение главной обратной связи АСУ по ошибке положительной вместо отрицательной, что практически при любых параметрах делает систему неустойчивой.
• Значительная инерционность элементов замкнутого контура АСУ (например, объекта управления), из-за которой в режиме колебаний системы сигнал главной обратной связи (например, управляемая величина) значительно отстает от входного сигнала (например, управляющего воздействия) и оказывается с ним в фазе. Это означает, что связь, выполненная конструктивно как отрицательная, в динамическом режиме (режиме гармонических колебаний) начинает на определенной частоте действовать как положительная. Это ведет к раскачиванию системы и нарушению ее устойчивости.

Задачами анализа устойчивости АСУ обычно являются:

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться: