
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Задачи моделирования по экпериментальным даннымСтр 1 из 10Следующая ⇒
Поэтому мы еще раз обратимся к постановке задач моделирования и подробно рассмотрим какие практические многомерные задачи возможно решать с помощью МНК, свойства метода, оценок МНК, преимущества и недостатки классических методов многомерного РА и возможные пути решения этих птроблем Современное моделирование (в том числе аналитическое) принято отслеживать от группы ученых связанных с Ньютоном, создавшего теорию бесконечно малых – Теорию Диференциального и Интегрального исчисления. Это удивительное прозрение практически впервые породило аналит ические математические модели в точности соотв-щие реальным физическим процессам. Он выдвинул гениальную по простоте и адекватности идею что значительное количество физических моделей макромира увязывают в своих взаимоотношениях линейные перемещения с их скоростями, ускорениями и тд и создал строгий аппарат обращения с данными величинами и уравнениями связвывающими эти величины. С помощью этого аппарата была решена грандиозная задача - задача моделирования движения тел небесной механики.
Паралельно эта задача породила к жизни сопутствующие направления исследований - теорию вероятности (ЛАГРАНЖ, МУАВР, БАЙЕС). Конечно ТВ имеет свои родные корни, связанные с изучением случайности, но вычислительные, практические аспекты ТВ стимулировала родственная «небесной механике» задачка из теории измерений. Именно ниже указанная задача стала первой сформулированной задачей статистического моделирования. Надо было наиболее точно определить начальные условия для реш задачи Неб Мех – то есть определить наиболее точное положение звезд на небосклоне по неоднократным их измерениям.. Таким образом в 1800-тых годах - Лаплас, Гаусс и Лежандр, каждый из которых в то время работал над теорией движения небесных тел и не мог обойти проблемы теории измерений предложили свои варианты решения такой задачи. Сначала о Лапласе. Лапласомбыло предложено оценивать неизвестное значение измеряемой величины Оказалось, что такое значение Позже, было показано что задача минимизации суммы модулей отклонений решаеться линейным программированием. О ЛП? Но в то время ученому сообществу более простой и технологичной показалась идея двух других французов – Гаусса и Лежандра которые для тех же условий задачи предложили минимизировать ф-нал
и предложили технологию Метода Наименьших Квадратов которую мы в общих чертах уже представляем. Ниже немного обобщим вгляд на эту технологию моделирования
Задачи моделирования по экпериментальным данным Исх. данные задачи моделивания - Модель в самом общем виде предполагем вида Делаем шаг упрощения задачи – предполагаем наличие в структуре переменных быстрых - х и медленных - а , то есть
а – параметрами модели
Напомним, что нам известно Любая задача моделированмя по экспериментальным данным начинается с данных – таблицы результатов эксперимента или таблицы наблюдений –
Итак, матрица данных имеет m столбцов и n строк, соответственно геометрическую интерпретацию регресии можно получить в пространстве столбцов или в пространстве строк = или что то же самое в пространстве переменных (оси –переменные) или в пространстве точек. (оси - номера точек)
Интерпретация в пространстве переменных (столбцов)
Идея регрессии пришла в математику из теории вероятности. ТВ по сути дала следующее определение понятию регресии у по х: регрессия у по х это матожидание СВ У с условной функцией распределение вероятности или с учетом, что у нас есть только конечная выборка аналогично регрессия х по у это матожидание СВ Х с условной функцией распределение вероятности Тогда использовав выборочные оценки мат. ожиданий как формулы для средних значений точек попавших в полосы
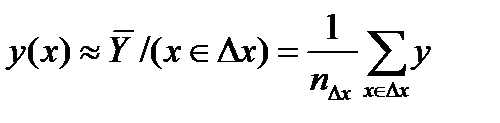 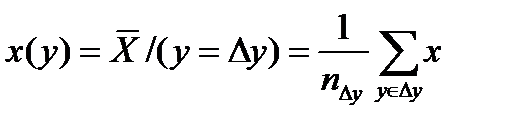
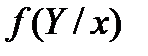 и и 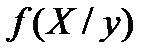 унимодальны и симметричны то по этим формулам для средних линий в полосах получим в каждом “яйце” точки, принадлежащие линии регрессии. Для каждой линии достаточно построить по 2 точки и мы их проведем. Обращаю внимание что регрессии у=f(x) и х=f(у) не совпадают? Они совпадут (центр. линия) – и регр превр в алгебру -когда рассеян симм отн бисктр и унимодальны и симметричны то по этим формулам для средних линий в полосах получим в каждом “яйце” точки, принадлежащие линии регрессии. Для каждой линии достаточно построить по 2 точки и мы их проведем. Обращаю внимание что регрессии у=f(x) и х=f(у) не совпадают? Они совпадут (центр. линия) – и регр превр в алгебру -когда рассеян симм отн бисктр и 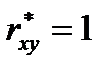
Свойство проективности МНК ( вывод осн ф-ла МНК, используя теперь свойство проективности) 1. Напомним, что применяя МНК для регресии мы оцениваем параметры регресии Здесь Напомним что дальнейшие результаты будут такие же, если мы вместо (1) будем рассматривать модель более общую модель Результаты будут верны с точностью до переобозначения. Поэтому, рассуждая в дальнейшем об (1) что формально проще, имеем далее в виду и (2) то есть модель нелинейную по аргументам регрессии. 2. Описывая данные задачи регрессии в виде таблиц естественно и выводить основные результаты в матричном виде (что бы не выделять отдельно своб член - ниже для упрощения записи - вектор Лапласом было предложено оценивать неизвестное значение измеряемой величины
Оказалось, что такое значение Позже, было показано что задача минимизации суммы модулей отклонений решаеться линейным программированием. О ЛП? Но в то время ученому сообществу более простой и технологичной показалась идея двух других французов – Гаусса и Лежандра которые для тех же условий задачи предложили минимизировать ф-нал
и предложили технологию Метода Наименьших Квадратов.
Несмещенность оценки Несмещенная оценка
Наиболее характерным примером смещенности оценки есть выборочная дисперсия
Но при Такую несмещенность называют асимптотической несмещенностью. А для дисперсии - состоятельной и несмещенной оценкой оказывается выборочная статистика именно для нее имеем Эффективность оценки Эффективная оценка – это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра Доказано, напимер что Что же получиться при нарушении всех или части из 1- 4 – свойств? –нарушаются перечисленные выше свойства (в разной мере) Если оценка не состоятельна это значит что мы ее не только неточно определяем, но вообще не то расчитываеим, а что расчитываем надо отдельно разбиратьься Если оценка смещена – то хорошо если только ассимтотически смещена. А е сли просто смещена надо постаратся разобратся в оценке смещения Наконец если оценка неэффективна – надо искать лучшую, эффективную. 3 ========================= Анализ остатков решения МНК Одним из распространенных приемов оценки условий применения МНК – это анализ остатков моделирования. И так есть табличные значения выхода Основные свойства проверяемые при анализе - - случайность остатков (равномерность распределения вдоль оси аргументов) -гомоскедатичность дисперсии остатков - нормальность частотного распределения остатков с нулевым МО - независимость остатков Случайность остатков Свойства проверяются путем анализа графиков остатков вдоль оси аргументов.
Если на графике получена горизонтальная полоса, то остатки случайные величины от найденной модели
хорошо аппроксимируют фактические значения y.
- Разброс (дисперсия) постоянна, МО –переменно и не равно 0.
- Дисперсия остатков переменна – гетероскедатична (в этом случае остатки тоже неслучайны)
- остатки характер
графиков остатков вошедших в уравнение регрессии: есть ли там зависимость или нет нам зависимости? По поводу анализа графиков - повторяем все то же что при анализе Добавим что: Скопление точек в определенных участках значений фактора xj говорит о наличии систематической погрешности модели. Во всех этих случаях необходимо либо менять базис расчета регрессии - функции 2.Гомоскедастичность дисперсии остатков Свойство проверяются путем анализа графиков дисперсии остатков вдоль оси аргументов (или по оси времени, если это процесс) Гетероскедастичность – непостоянство дисперсии можно демонстрировать как в координатах (у-х) так и в координатах ( Типичные варианты гетероскедастичности - Возрастание по параметру
А) в координатах (у-х) Отклонения от модели растут по мере увеличения x.
получаем вид - имеем большую дисперсию ост. для больших значений
А) в координатах (у-х)
и далее однородна по мере увеличения x.
А ) в координатах (у-х)
Л
3.Проверка нормальности частотного распределения остатков ИТАК Имеем выборку из данных объёма n Как вы помните критерием согласия называют критерий по которому проверяют соответствие (согласие) тестируемого распределения (нашей выборки остатков) гипотезе. В нашем случае гипотеза – нормальное распределение. Функция распределения Для того что-бы определить какому именно Нормальному Распределению необходимо проверить соответствие, ----- то в предположении, что наше распределение нормально – вычисляют выборочные его параметры –оценку МО – среднее Имеется несколько критериев согласия. Наиболее часто используют критерий согласия К.Пирсона («хи-квадрат») .
По выборке остатков рассчитывают эмпирическое распределение: это эмпирические частоты. с серединами в точках Рассчитывают выборочные
В предположении нормального распределения генеральной совокупности Пример При уровне значимости 0, 05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты: Эмпирические частоты: 6 13 38 74 106 85 30 14 Теоретические частоты: 3 14 42 82 99 76 37 13 Рассчитаем Таблица критических точек распределения Пирсона.
Так как Напомним еще раз упоминавшуюся выше проблему; Так как в механизме оценки степени отличия распределений по В инете вы найдете море критического материала по поводу применения теории стат гипотез «неграмотными» специалистами на объемах выборки 40, 50, 70 и даже более пациентов. Однако к счастью для этих исследователей (просто часто они не в курсе) существует результат, позволяющий резко ограничить объем необходимой выборки для получения достоверного ответа о нормальности проверяемого распределения Рассмотрим на практике основной подход к определению нормальности распределения: правило 3 сигма . Если внешне ваше распределение не сильно отличается от нормального то утвердится в этом дает возможность правило 3 сигма.
Закона вероятность попадання СВ за пределы отклонения от МО на 3σ, Поэтому, если оцениваемое распределение «на глаз не сильно отличается от нормального» то на практике вместо применения теории Стат проверки гипотез применяют правило 3σ в обратную сторону Если в интервал 3σ попадает не менее 99, 7% реализаций то рассматриваемое распределение нормально. Правило «двух сигм». С вероятностью близкой к единице (0, 9544) можно утверждать, что значения нормально распределенной СВ лежат в интервале то есть, если проведено 10 000 испытаний, то результаты 9544 испытаний должны принадлежат указанному промежутку Вот теперь поставим вопрос - а какое минимальное количество испытаний достаточно провести для того чтобы убедится в нормальности распределения исходя из правила «двух сигм» (альфа = 0.95 ) Применение гипотеза Хилла для оценки минимально необходимого объема выборки. Клюшин Дмитрий Анатольевич, Доказательная медицина. Применение статистических методов. Пусть Основной распределеной массой Пусть выполнено следующее: 1. Для получения выборки Напомним: вариационный ряд - это выборка 2.Выборочные значения Тогда выполняется гипотеза Хилла:
(Все доказательства пока опустим) Теорема 1 Если
Теорема 2. Если при
уровнем значимости α, как он введен выше. Уровень значимости определен так, что 5% точек попадает в хвосты. Значит, считая что хотя бы 1 интервал вариационного ряда попал какой-то из 2-х хвостов (это определяет минимальное количество точек в выборке, что-бы данное событие произошло) то можно написать что Отсюда при α =0, 05 имеем То мы нашли минимальное количество испытаний достаточное для проверки утверждения: если полученные ??????? Данное утверждение находит связь между значимостью результата (0.05) и минимальным количеством точек, которые нужны для утверждения гипотезы допустим Н0. Условием корректности применения оценки для n есть симметричность и непрерывность рассматриваемых распределений. Это дает наконец точку опоры для применения теории статичтических гbпотез для относительно небольшиз размеров выборки. Небольшое отвлечение - Об условиях применения гипотезы Хилла - напомним она применима к СВ которые имеют симметричные и абсолютно непрерывные плотности распределения
рис 33 Канторова лестница - граффик массы канторова стержня от коорд-ы х канторов стержень - стержень масса которого пропорциональна мощности канторова множества Канторово множество
C=⋂ Сi i=0,...∞ называется Канторовым множеством. Из единичного отрезка C0=[0, 1] удалим среднюю треть, то есть интервал (1/3, 2/3). Оставшееся точечное множество обозначим через C1. Множество C1=[0, 1/3]∪ [2/3, 1] состоит из двух отрезков; удалим теперь из каждого отрезка его среднюю треть, и оставшееся множество обозначим через C2. Повторив эту процедуру опять, удаляя средние трети у всех четырёх отрезков, получаем C3. Дальше таким же образом получаем последовательность замкнутых множеств C0⊃ C1⊃ C2⊃ …. Пересечение СВ с Пл Р как видоизм кантор лестница рис. 33 - будет непр но не абсолютно непрерывна 4 Независимость распределения остатков
где
где к -сдвиг, D- дисперсия остатков. По смыслу это коэффициент корреляции между остатками со сдвигом с к шагами. То есть чем он больше тем жеще лин связь между остатками и меньше речи обм их независимости. Для конечного ряда
Автокор через несмещ оценку дисперсии
Если АВКФ будет похожа на ниже приведенную -
то все хорошо – остатки похоже независимы (надо только помнить что автокорреляция проверяет только линейную независимость величин, независимы ли они на самом деле – вопрос более сложного анализа) Любые другие варианты – плохо Например практически незатухающий график АКФ ряда свидетельствует о наличии сильного неучтенного в модели тренда.
Вот здесь есть умеренный тренд и неясно выраженной сезонностью
А здесь сильная периодическая составляющая осталась в остатках – ее можно вытащить – об этом позже
5=============???? 4 лист или плюс
Критерий Маллоуза Критерий Маллоуза оказываеся дает при этом несмещенную оценку ошибки прогнозирования , Но надо знать дисп шума 2. Пусть известно распределение шума Когда известно распределение шума Для нахождения параметров
где В частном случае нормального шума он принимает вид критерия Маллоуза. При этом на практике он применяется в упрощенном виде
Этот вариант формулы называют критерием Акаике-Маллоуза Данный критерий существенно ограничивает рост сложности модели наличием аддитивного члена 2s. Однако проблема применения состоит в том, что в практических задачах функция распределения шума да часто и его дисперсия неизвестны. А что тогда делать? Используют тогда менее обонованные но практически неплохо работающие критерии 3. Байесовский информационный критерий (критерий Шварца):
4. Также популярен критерий финальнрй ошибки предсказания Акаикеприменяемійпри неизвестном характнрн шума и ккорректирующий остаточную сумму квадратов ошибки Покажем это Итак, по формулировке 1. – имеем
Предположим обратное, что для некоторого Тогда И при этом по определению не является истинным аргументом. Когда такое возможно? – либо это случайность (генератор так случайно сгенерировал для них |
Последнее изменение этой страницы: 2017-04-12; Просмотров: 543; Нарушение авторского права страницы