
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Напомним осн. правила матричных операций
1.– Умножения – А*В=С - 2. Траспонирование – столбцы делает строками, строки столбцами (в квадратной матрице – просто зеркально отображаем относительно гл диагонали) кроме того: (АВ)Т=ВТ АТ и следствие (АВС)Т=СТВТАТ 3.Обратная матрица А-1 матрицы А это такая матрицадля которой выполняется
4.Свойство ортогональности векторов а и в:
………… в n -ой точке - На самом деле выполнить их невозможно ввиду предположения Эти условия (требования) (*) в матричном виде можно записать как
Для решения задачи регрессии среди всех моделей Матричную запись модели То есть в результате решения мы находим такие
Если выражение, которое нам надо приблизить в матричном виде выглядит как
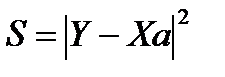 . Эта ошибка . Эта ошибка 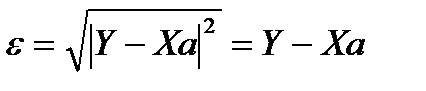 есть расстояние от вектора есть расстояние от вектора 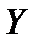 до вектора до вектора 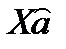 . . Вектор Отыскание решения
которая лежит ближе всего к Таким образом, вектор Далее для упощения записи вывода формулы МНК отрбросим значки “тильда” Ортоганальность вектора невязки
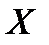 есть обязательно линейная комбинация столбцов с некоторыми коэффициентами есть обязательно линейная комбинация столбцов с некоторыми коэффициентами 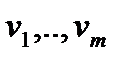 , то есть это вектор , то есть это вектор 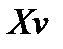 . .
При произвольном
Для всех
Так как это равенство должно быть справедливо для произвольного вектора Таким образом мы нашли сооошение дающее решение по МНК несовместной системы условных уравнений
которая называется системой нормальных уравнений Если столбцы матрицы
Правда, естественно, решение не в том смысле, что оно превращает его в равенство, а в том, что в пространстве
Что и есть решение – основная народнохозяйственная ф-ла МНК (брать производн. ф-ла,, приравн его=0, решать систему– проверте на примерах).То есть машина производных не берет а реалмзует полученную матричную формлу различными вычисдтельными процедурами. Самое слабое место – обращение матрицы, особенно при ее плохой обусловленности (корр переменных) – это будет у нас отдельный разговор. *2 ====== Оператор проектирования. Свойства оператора. Полученный результат имеет полезное для приложений свойство – Из выражение Проекция вектора
Матрица называется матрицей проектирования вектора Посмотрите какой интересный вид у нее. Эта матрица имеет два основных свойства: 1. она идемпотентна 2. она симметрична - Проверим 1. 2.по 2
Очень важно что верно и обратное: матрица Р, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов Х произвольного вектора У. Данные свойства могут использоватся при проверке корректности использования МНК (в первую очередь зашумленность данных) - потеря указанных свойств матрицей Р служит сигналом что оценки МНК (в силу нарушения условий применения - о них ниже ) потеряли свое качество – Состоятельность, несмещеность и эффективность Именно эти наруш єтих св - вызывают необходимость корректировки расчета, отыскания новых регрессоров, фильтрации шумов, расчета нескольких уравнений регресии вместо одного и т.д. о чем вам расказывал ЕА Все это делается для минимизации минимизации последствий нарушения условий применения МНК (а они, как увидим нарушаются практически всегда). |
Последнее изменение этой страницы: 2017-04-12; Просмотров: 423; Нарушение авторского права страницы