
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Частотный косвенный метод оценки качества.
1. Близким по виду вещественным характеристикам Р(w) соответствуют близкие по виду переходные характеристики h(t). 2. При косвенных оценках вещественной характеристики Р(w) ограничиваются исследованием спектра частот wП, при которых вещественная действительная характеристика Р(w) имеет положительное значение.
3.
Если  , где п – произвольное число, то , где п – произвольное число, то 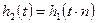 . Это означает следующее: если рассмотреть две характеристики, то . Это означает следующее: если рассмотреть две характеристики, то
вещественной частотной характеристике с захватом наибольших спектров частот (более широкая переходная характеристика) соответствует менее длительный переходный процесс. Чем шире Р(w), тем быстрее происходит затухание, т.е. тем меньше время переходного процесса. 4. Установившееся значение h(¥ ) соответствует значению вещественной частотной характеристики при частоте w=0
5. Если вещественная частотная характеристика Р(w) является монотонно убывающей функцией и Р(¥ )=0, то переходная характеристика имеет апериодический характер. Для апериодического процесса
В этом случае перерегулирование  . .
6. Если Р(w) - является положительной невозрастающей функцией, то переходная характеристика имеет вид затухающих колебаний:
Перерегулирование составляет 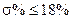 . .
7. Если вещественная характеристика Р(w) имеет явно выраженный max
то переходная характеристика будет иметь вид затухающих колебаний и перерегулирование 8. Общим условием для немонотонности переходной характеристики (колебательности) является: частотная характеристика Р(w) на каком-то этапе должна быть меньше G(w), которая определяется как
Здесь 9.
Если Р(w) претерпевает разрыв, то система находится на границе устойчивости. 10.
Склонность к колебаниям (hmax) тем выше, чем больше пик Pmax. 11. Для монотонного (апериодического переходного процесса) время переходного процесса составляет
12. Если Р(w) может быть аппроксимирована трапецией вида
13.
где Pk(w) - значение высоты трапеции, имеющей на осях Р(w), w - положительное значение, Pi(w) - значение высоты трапеции, имеющей на осях Р(w), w - отрицательное значение.
Построение вещественной частотной характеристики с использованием ЛАЧХ разомкнутой системы и номограммы.
Рассмотрим структурную схему:
Передаточная функция такой системы имеет вид:
Данному уравнению на комплексной плоскости соответствуют кривые Р(w)=const, при этом по оу откладываются 20lgH, а по ох – фаза q.
Данная схема называется номограммой. Индексы около каждой кривой означают значения вещественной частотной характеристики (ВЧХ).
Алгоритм построения ВЧХ по номограмме 1. Строятся ЛАЧХ и ФЧХ разомкнутой системы. 2. Заполняется следующая таблица (первые три строки):
3. Строится ЛАФХ в масштабе номограммы. 4. Данная ЛАФХ накладывается на номограмму. 5. Точки пересечения ЛАФХ с кривыми номограммы определяют значение ВЧХ. Заполняем четвертую строку данной таблицы. Т.о. получаем затабулированную функцию Р(w).
Корневые методы оценки показателей качества
Корневые методы для определения косвенной оценки показателя качества используют корни характеристического уравнения замкнутой системы и их расположения на комплексной плоскости. Передаточная функция любой системы может быть представлена в следующем виде:
где gi – это нули передаточной функции; li – полюса передаточной функции (корни характеристического уравнения). li определяет устойчивость системы и качество переходных процессов, gi определяет только качество переходных процессов.
|
Последнее изменение этой страницы: 2017-05-06; Просмотров: 536; Нарушение авторского права страницы