Расчетные параметры распределения

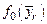
n1 n2 n3 n4 n5 n6 n7 n8	–2, 746 –1, 964 –1, 183 –0, 402 0, 379 1, 161 1, 942 2, 723	0, 0004 0, 0017 0, 0026 0, 0091 0, 0087 0, 0052 0, 0004 0, 0004	0, 0092 0, 0579 0, 1982 0, 3680 0, 3710 0, 2036 0, 0603 0, 0099	0, 0002 0, 0013 0, 0044 0, 0082 0, 0083 0, 0045 0, 0013 0, 0002

 

· по результатам расчета строятся гистограмма, графики и (рис. 2.2).

 

Проверка согласия между эмпирическим и теоретическим (нормальным) распределениями по критерию Пирсона. Как следует из анализа интервального вариационного ряда (табл. 2.6), для применения критерия Пирсона необходимо объединить интервалы 1 и 2, интервалы 7 и 8 с интервалом 6, так как в интервалах 1, 2, 7, 8 количество наблюдений менее 5. В результате объединения получим следующий ряд распределения (табл. 2.8):

 

Таблица 2.8

Объединенный интервальный ряд

Интервалы	48, 8…118, 8	118, 8… 153, 8	153, 8… 188, 8	188, 8… 223, 8	223, 8… 328, 8
mi = ni

 

Рис. 2.2

 

Определим вероятность . Вероятность р₁ выражает вероятность того, что случайная величина Х, имеющая нормальный закон распределения, принимает значение, принадлежащее интервалу (48, 8…118, 8), т.е.

 

где Ф (t) определяется по табл. П4 Приложения. Аналогично получаем:

; ; ; .

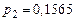Для нахождения статистики составим табл. 2.9.

Таблица 2.9

Расчет статистики c²

№ п/п	Интервал после объединения	mi	рi	nрi
	48, 8…118, 8		0, 0574	3, 79	1, 21	1, 46	0, 385
	118, 8…153, 8		0, 1565	10, 33	4, 33	18, 75	1, 815
	153, 8…188, 8		0, 2813	18, 57	2, 43	5, 90	0, 318
	188, 8…223, 8		0, 2834	18, 70	1, 30	1, 69	0, 090
	223, 8…328, 8		0, 2197	14, 50	0, 50	0, 25	0, 017
S			0, 9983	65, 89			2, 625 = c2

 

Количество интервалов r = 5, количество параметров распре-деления – s = 2, число степеней свободы k = r – s – 1 =
= 5 – 2 – 1 = 2. В табл. П3 Приложения для уровня значимости и k = 2 соответствует c . Имеем 9, 2 > 2, 625, следовательно, нет оснований отвергнуть гипотезу о нормальности распределения ресурса.

Вероятность безотказной работы детали. Значение среднего ресурса R при нормальном распределении численно равно математическому ожиданию:

R = m_l = 189, 3 тыс.часов.

Рассчитаем вероятность безотказной работы детали по интервалам наработки (табл. 2.6) по формуле

;

P(l₁) = (66 – 1)/66 = 0, 98; P(l₂) = (66 – 5)/66 = 0, 92;

P(l₃) = (66 – 11)/66 = 0, 83; P(l₄) = (66 – 32)/66 = 0, 52;

P(l₅) = (66 – 52)/66 = 0, 21; P(l₆) = (66 – 64)/66 = 0, 03;

P(l₇) = (66 – 65)/66 = 0, 015; P(l₈) = (66 – 66)/66 = 0.

На рис. 2.3 построена кривая вероятности безотказной работы детали P(l) в зависимости от наработки l.

Рис. 2.3

Литература

 

1. Зорин В.А.Основы работоспособности технических систем: учебник для вузов/ М-во образования и науки Рос. Федерации / М-во образования и науки Рос. Федерации — М.: Магистр-Пресс, 2005. — 536с.

2. Шубин, В.С., Рюмин Ю.А.Надежность оборудования химических и нефтеперерабатывающих производств: учеб. пособие для вузов — М.: Химия: КолосС, 2006. — 359с. — [Учебники и учебные пособия для студентов высших учебных заведений]

3. Половко, А.М., Гуров С.В.Основы теории надежности: учеб. пособие для вузов — Изд. 2-е, перераб. и доп. — СПб.: БХВ-Петербург, 2006. — 704с.

4. Животкевич И.Н., Смирнов А.П.Надежность технических изделий [Электронный ресурс] — М.: Термика: ИК " Кодекс", 2004. — 1 электрон. опт. диск (CD-ROM)

 

ПРИЛОЖЕНИЯ

Т а б л и ц а П1

 

Нормированная функция нормального распределения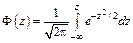

z 0, 0 –0, 1 –0, 2 –0, 3 –0, 4 –0, 5 –0, 6 –0, 7 –0, 8 –0, 9 –1, 0 –1, 1 Ф(z) 0, 500 0, 460 0, 421 0, 382 0, 345 0, 309 0, 274 0, 242 0, 212 0, 184 0, 159 0, 136

z –1, 2 –1, 3 –1, 4 –1, 5 –1, 6 –1, 7 –1, 8 –1, 9 –2, 0 –2, 1 –2, 2 –2, 3 Ф(z) 0, 115 0, 097 0, 081 0, 067 0, 055 0, 045 0, 036 0, 029 0, 023 0, 018 0, 014 0, 011

z –2, 4 –2, 5 –2, 6 –2, 7 –2, 8 –2, 9 –3, 0 –3, 1 –3, 2 –3, 3 –3, 4 Ф(z) 0, 008 0, 006 0, 005 0, 004 0, 003 0, 002 0, 0013 0, 0011 0, 0007 0, 0005 0, 0003

z –3, 5 –3, 6 –3, 7 –3, 8 –3, 9 Ф(z) 0, 0002 0, 0002 0, 0001 0, 0001 0, 000

 

z 0, 0 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 1, 0 1, 1 Ф(z) 0, 500 0, 540 0, 579 0, 618 0, 655 0, 691 0, 726 0, 758 0, 788 0, 816 0, 841 0, 864

z 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 2, 1 2, 2 2, 3 Ф(z) 0, 885 0, 903 0, 919 0, 933 0, 945 0, 955 0, 964 0, 971 0, 977 0, 982 0, 986 0, 989

z 2, 4 2, 5 2, 6 2, 7 2, 8 2, 9 3, 0 3, 1 3, 2 3, 3 3, 4 Ф(z) 0, 992 0, 994 0, 995 0, 996 0, 997 0, 998 0, 9987 0, 9990 0, 9993 0, 9995 0, 9997

z 3, 5 3, 6 3, 7 3, 8 3, 9 Ф(z) 0, 9998 0, 9998 0, 9999 0, 9999 1, 000

Примечание. Параметры z и Ф(z) расположены парами, т.е. для каждого z под ним дан параметр Ф(z). Положительные параметры z отделены от отрицательных параметров двойной линейкой.

 

Т а б л и ц а П2

Плотность вероятности нормального распределения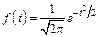

t
0, 0	0, 3989
0, 1
0, 2
0, 3
0, 4
0, 5
0, 6
0, 7
0, 8
0, 9
1, 0	0, 2420
1, 1
1, 2
1, 3
1, 4
1, 5
1, 6
1, 7
1, 8
1, 9
2, 0	0, 0540
2, 1
2, 2
2, 3
2, 4
2, 5
2, 6
2, 7
2, 8
2, 9
3, 0	0, 0044
3, 1
3, 2
3, 3
3, 4
3, 5
3, 6
3, 7
3, 8
3, 9

 

 

Т а б л и ц а П3

a

Значения c² в зависимости от вероятности P (c2 > c² ) и числа степеней свободы k

Число стпеней свободы k	Вероятность
0, 99	0, 98	0, 95	0, 90	0, 80	0, 70	0, 50	0, 30	0, 20	0, 10	0, 05	0, 02	0, 01	0, 001
	0, 00016	0, 001	0, 004	0, 016	0, 064	0, 148	0, 455	1, 074	1, 642	2, 71	3, 84	5, 41	6, 64	10, 83
	0, 020	0, 040	0, 103	0, 211	0, 446	0, 713	1, 386	2, 41	3, 22	4, 60	5, 99	7, 82	9, 21	13, 82
	0, 115	0, 185	0, 352	0, 584	1, 005	1, 424	2, 366	3, 66	4, 64	6, 25	7, 82	9, 84	11, 34	16, 27
4	0, 297	0, 429	0, 711	1, 064	1, 649	2, 20	3, 36	4, 88	5, 99	7, 78	9, 49	11, 67	13, 28	18, 46
	0, 554	0, 752	1, 145	1, 610	2, 34	3, 00	4, 35	6, 06	7, 29	9, 24	11, 07	13, 39	15, 09	20, 5
	0, 872	1, 134	1, 635	2, 20	3, 07	3, 83	5, 35	7, 23	8, 56	10, 64	12, 59	15, 03	16, 81	22, 5
	1, 239	1, 564	2, 17	2, 83	3, 82	4, 67	6, 35	8, 38	9, 80	12, 02	14, 07	16, 62	18, 48	24, 3
	1, 646	2, 03	2, 73	3, 49	4, 59	5, 53	7, 34	9, 52	11, 03	13, 36	15, 51	18, 17	20, 1	26, 1
	2, 09	2, 53	3, 32	4, 17	5, 38	6, 39	8, 34	10, 66	12, 24	14, 68	16, 92		21, 7	27, 9
	2, 56	3, 06	3, 94	4, 86	6, 18	7, 27	9, 34	11, 78	13, 44	15, 99	18, 31	21, 2	23, 2	29, 6
	3, 05	3, 61	4, 58	5, 58	6, 99	8, 15	10, 34	12, 90	14, 63	17, 28	19, 68	22, 6	24, 7	31, 3
	3, 57	4, 18	5, 23	6, 30	7, 81	9, 03	11, 34	14, 01	15, 81	18, 55	21, 0	24, 1	26, 2	32, 9
	4, 11	4, 76	5, 89	7, 04	8, 63	9, 93	12, 34	15, 12	16, 98	18, 81	22, 4	25, 5	27, 7	34, 6
14	4, 66	5, 37	6, 57	7, 79	9, 47	10, 82	13, 34	16, 22	18, 15	21, 1	23, 7	26, 9	29, 1	36, 1
	5, 23	5, 98	7, 26	8, 55	10, 31	11, 72	14, 34	17, 32	19, 31	22, 3	25, 0	28, 3	30, 6	37, 7
	5, 81	6, 61	7, 96	9, 31	11, 15	12, 62	15, 34	18, 42	20, 5	23, 5	26, 3	29, 6	32, 0	39, 3
	6, 41	7, 26	8, 67	10, 08	12, 00	13, 53	16, 34	19, 51	21, 6	24, 8	27, 6	31, 0	33, 4	40, 8
	7, 02	7, 91	9, 39	10, 86	12, 86	14, 44	17, 34	20, 6	22, 8	26, 0	28, 9	32, 3	34, 8	42, 3
	7, 63	8, 57	10, 11	11, 65	13, 72	15, 35	18, 34	21, 7	23, 9	27, 2	30, 1	33, 7	36, 2	43, 8
	8, 26	9, 24	10, 85	12, 44	14, 58	16, 27	19, 34	22, 8	25, 0	28, 4	31, 4	35, 0	37, 6	45, 3
	8, 90	9, 92	11, 59	13, 24	15, 44	17, 18	20, 3	23, 9	26, 2	29, 6	32, 7	36, 3	38, 9	46, 8
	9, 54	10, 60	12, 34	14, 04	16, 31	18, 10	21, 3	24, 9	27, 3	30, 8	33, 9	37, 7	40, 3	48, 3
	10, 20	11, 29	13, 09	14, 85	17, 19	19, 02	22, 3	26, 0	28, 4	32, 0	35, 2	39, 0	41, 6	49, 7
24	10, 86	11, 99	13, 85	15, 66	18, 06	19, 94	23, 3	27, 1	29, 6	33, 2	36, 4	40, 3	43, 0	51, 2
	11, 52	12, 70	14, 61	16, 47	18, 94	20, 9	24, 3	28, 2	30, 7	34, 4	37, 7	41, 7	44, 3	52, 6
	12, 20	13, 41	15, 38	17, 29	19, 82	21, 8	25, 3	29, 2	31, 8	35, 6	38, 9	42, 9	45, 6	54, 1
	12, 88	14, 12	16, 15	18, 11	20, 7	22, 7	26, 3	30, 3	32, 9	36, 7	40, 1	44, 1	47, 0	55, 5
	13, 56	14, 85	16, 93	18, 94	21, 6	23, 6	27, 3	31, 4	34, 0	37, 9	41, 3	45, 4	48, 3	56, 9
	14, 26	15, 57	17, 71	19, 77	22, 5	24, 6	28, 3	32, 5	35, 1	39, 1	42, 6	46, 7	49, 6	58, 3
	14, 95	16, 31	18, 49	20, 6	23, 4	25, 5	29, 3	33, 5	36, 2	40, 3	43, 8	48, 0	50, 9	59, 7

 

Т а б л и ц а П4

Значение функции

t
0, 0	0, 0000	0, 0080	0, 0160	0, 0239	0, 0319	0, 0399	0, 0478	0, 0558	0, 0638	0, 0717
0, 1
0, 2
0, 3
0, 4
0, 5
0, 6
0, 7
0, 8
0, 9
1, 0	0, 6827	0, 6875	0, 6923	0, 6970	0, 7017	0, 7063	0, 7109	0, 7154	0, 7199	0, 7243
1, 1
1, 2
1, 3
1, 4
1, 5
1, 6
1, 7
1, 8
1, 9
2, 0	0, 9545	0, 9556	0, 9566	0, 9576	0, 9586	0, 9596	0, 9606	0, 9616	0, 9625	0, 9634
2, 1
2, 2
2, 3
2, 4
2, 5
2, 6
2, 7
2, 8
2, 9
3, 0	0, 0073	0, 9974	0, 9975	0, 9976	0, 9976	0, 9977	0, 9978	0, 9979	0, 9979	0, 9980
3, 1
3, 2
3, 3
3, 4
3, 5
4, 0	0, 999936	0, 9999
5, 0	0, 99999994	–	–	–	–	–	–	–	–	–

 

 

⇐ Предыдущая123456

Поделиться: