
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Тема 6. ИСПОЛЬЗОВАНИЕ КРИТЕРИЯ ХИ–КВАДРАТ
Анализируя наследственные признаков у гороха, Г.Мендель выявил закономерности расщепления фенотипов: при моногибридном скрещивании 3:1; при дигибридном скрещивании 9:3:3:1, при анализирующем скрещивании – 1:1 или 1:1:1:1. Следует помнить, что в опытах с растительными и животными объектами такие идеальные соотношения получаются далеко не всегда, особенно, если потомство малочисленное. Например, провели 3 серии аналогичных скрещивании и получили результаты: 30 : 10; 25 : 11; 32 : 7. Чтобы проверить, является ли наследование признаков случайным или оно все же подчиняется идеальному соотношению 3:1, применяют статистические методы, самым популярным из которых является критерий значимости - ХИ -квадрат. (χ2). Функция χ2 определяется следующим уравнением:
Н - наблюдаемое значение О - ожидаемое значение Символ
Решение задач с применением ХИ–квадрата Задача 1. У лабораторных мышей темный цвет глаз доминирует над розовым: Т- темные глаза; t - розовые глаза. При моногибридном скрещивании, получив потомство F1, скрестили гетерозиготные формы между собой. Среди потомства F2 получено 787 темноглазых и 277 розовоглазых особей.
3/4 - должно быть с темными глазами;
темн. розов. Заполняем таблицу:
Вопрос: можно ли разность между теоретически ожидаемой величиной и реально полученной (в опыте) рассматривать как случайность, а само расщепление как соответствие законам Менделя? Чтобы ответить на этот вопрос, необходимо познакомиться с такими понятиями как: · число степеней свободы; · уровень достоверности.
Уровень достоверности. В силу разных случайных причин (не все зиготы при многоплодной беременности выжили; иногда крысы и мыши съедают часть приплода; у растений не вся созревшая пыльца принимает участие в оплодотворении; птицы могут склевать часть семян и т.п.), небольшая часть потомства может остаться не проанализированной, в результате получаются небольшие различия между ожидаемыми и наблюдаемыми значениями. Уровень достоверности оценивается в процентах (5%, 1%, 0,1%)
Число степеней Свободы |
Уровень достоверности | ||||||||||||||||||||||||||
| 5% | 1% | 0,1% | |||||||||||||||||||||||||
| 1 | 3,84 | 6,64 | 10,83 | ||||||||||||||||||||||||
| 2 | 5,99 | 9,21 | 13,82 | ||||||||||||||||||||||||
| 3 | 67,82 | 11,34 | 16,27 | ||||||||||||||||||||||||
| 4 и т.д. до 10 | 9,49 | 13,28 | 18,47 | ||||||||||||||||||||||||
В задаче 1 степень свободы, χ2 = 0,59, а это меньше 5%-го уровня достоверности (3,84), значит расхождение допустимо, эксперимент согласуется с законом Менделя.
Задача 2.
При скрещивании пестрого петуха с пестрой курицей получено 38 цыплят с разной окраской оперения:
| Наблюдаемые значения (Н) | Черные 11 | Пестрые 18 | Белые 9 | Всего: 38 |
| Ожидаемые значения (О) | 38*1/4=9,5 | 38*2/4=19 | 38*1/4=9,5 | 38 |
| Разница Н-О | +1,5 | -1 | -0,5 | |
| (Н-О)2 | 2,25 | 1 | 0,25 | |
 (Н-О)2
О (Н-О)2
О
| 2,25/9,5=0,24 | 1/19=0,05 | 0,25/9,5=0,03 |
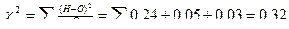
 Необходимо найти число степеней свободы: Ф-1 .У нас 3 фенотипа цыплят (черные, пестрые, белые), следовательно, 3-1=2.
Необходимо найти число степеней свободы: Ф-1 .У нас 3 фенотипа цыплят (черные, пестрые, белые), следовательно, 3-1=2.
Находим по таблице значения χ2 при двух степенях свободы. Для 5%-го уровня достоверности значение составляет 5,99, а это меньше рассчетного - 0,32.
Ответ: расхождение между теоретически ожидаемыми и экспериментально полученными значениями допустимо, отклонения можно считать случайными, а сам эксперимент согласуется с законами Менделя.
Задача 3.
Скрестили дигетерозиготных стрекоз с нормальными крыльями и темной окраской глаз. Во втором поколении наблюдали следующее распределение:
| Наблюдаемые значения (Н) | Норм.крылья, темные глаза: 268 | Корот.крылья, темные глаза: 50 | Норм. крылья, яркие глаза: 54 | Корот.крылья, яркие глаза: 28 | Всего: 400 |
| Ожидаемые значения (О) | 400 * 9/16 = 225 | 400 * 3/16 = 75 | 400 * 3/16 = 75 | 400 * 1/16 = 25 | 400 |
| Разница Н-О | +43 | -25 | -21 | +3 | |
| (Н-О)2 | 1849 | 625 | 441 | 9 | |
 (Н-О)2
О (Н-О)2
О
| 1849/225= 8,22 | 625/75= 8,33 | 441/75= 5,88 | 9/25= 0,36 |
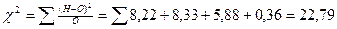
Находим число степеней свободы: 4 фенотипа потомства – 1 = 3.
Смотрим по таблице значений χ2 при 3 степенях свободы: 22,79>7,82>11,34>16,27
Ответ: В данном опыте нельзя говорить о соблюдении закона независимого расщепления.
Последнее изменение этой страницы: 2019-03-31; Просмотров: 274; Нарушение авторского права страницы