Понятие поверхности. Ориентация поверхности

С понятием поверхности мы уже встречались, в частности, когда знакомились с поверхностями второго порядка, с понятиями касательной плоскости и нормали, а также при изучении двойного интеграла. При изучении касательной плоскости мы брали простую поверхность, заданную явным уравнением , где . И говорили, что если функция  имеет в области  непрерывные частные производные 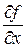, , одновременно не обращающиеся в нуль, то в любой точке нашей поверхности  существует касательная плоскость, и перпендикулярный ей вектор – нормальный вектор. Но когда мы изучали поверхности второго порядка, то у нас встречались другие способы задания поверхности, например , то есть неявное задание поверхности . Для такого задания можно выйти из положения, используя теорию неявных функций. Если в некоторой точке поверхности , производная по переменной  непрерывна и , то в некоторой малой окрестности этой точки, по теореме о существовании неявной функции, уравнение  может быть разрешено относительно переменной , при этом график выражения  можно рассматривать как простую поверхность.

Напомним, как мы строили касательную плоскость и нормальный вектор. Брали, на поверхности произвольную точку , проводили через неё всевозможные кривые по поверхности и строили к ним касательные прямые в данной точке. Если все эти касательные линии к нашим кривым лежат в одной плоскости, то она и будет называться касательной плоскостью. При этом вектор нормали будет направлен перпендикулярно этой плоскости. Заметим, что перпендикуляра (нормального вектора) к касательной плоскости в данной точке может быть построено два, имеющих противоположные направления. Таким образом, мы приходим к понятию стороны поверхности, которая может определяться выбором направления нормали.

Будем считать, что на нашей поверхности одна из сторон выделена. Обычно это делают так: в какой-то точке поверхности строят вектор, перпендикулярный поверхности (такой вектор называют «нормальным» вектором, или «нормалью»; похоже, что те, кто придумывал этот термин, считали, что для вектора самое нормальное расположение – по перпендикуляру к поверхности). Лучше всего считать, что этот вектор имеет некоторую заранее известную длину; чаще всего считают, что она равна 1. Когда мы передвигаемся по плоскости, вместе с нами передвигается и вектор нормали. Та сторона, на которой стоит вектор, и считается выделенной. Некоторые математики утверждают, что встречаются поверхности, для которых таким образом выделить сторону невозможно. Утверждают даже, что некто Мебиус гулял когда-то по такой поверхности вместе со своей любимой собакой, привязал ее к дереву и решил немного побродить в одиночестве. Через какое-то время он понял, что собака лает как раз под его ногами! Что же в этом случае делать? Я предлагаю считать такие поверхности несуществующими – по крайней мере, в нашей жизни; кому такая встретится, пусть выкручивается, как хочет.

Двусторонние поверхности

Возьмем на гладкой поверхности  произвольную точку 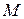, проведем в этой точке нормаль к поверхности и выберем одно определенное направление нормали. Начнем теперь непрерывно перемещать точку  по замкнутому контуру, лежащему на поверхности  и не пересекающему ее границы, приписывая каждому из ее положений, то из двух возможных направлений, в которое непрерывно переходит исходное положение нормали. В прежнее положение точка 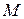 вернется либо с тем же направлением нормали, что и

Рис. 1 – Нормаль к поверхности                      исходное, либо с прямо противоположным направлением нормали (рис. 1).

Определение. Если на поверхности  есть хотя бы одна точка и хотя бы один не пересекающий границу поверхности контур, при обходе по которому направление нормали в точке меняется на противоположное, то поверхность  называется односторонней. Примером такой поверхности может служить лист Мебиуса, модель которого изображена на рисунке (рис. 2).

Определение. Если для любой точки поверхности  и любого замкнутого, не пересекающего границы поверхности  контура после обхода направление нормали не меняется, то поверхность называется двусторонней, а совокупность всех точек поверхности с выбранными в них по непрерывности направлениями нормали называется стороной такой поверхности.

Для двусторонней поверхности выбор направления нормали в одной ее точке определяет направления нормалей во всех точках поверхности, то есть определяет сторону поверхности.

Примерами двусторонних поверхностей могут служить любая плоскость, сфера, эллипсоид, параболоид, любая поверхность, задаваемая уравнением ,

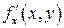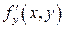Рис. 2 – Лист Мёбиуса                            где ,  и  – функции, непрерывные в некоторой области  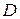плоскости  и так далее.

В дальнейшем мы рассматриваем только двусторонние поверхности.

Пусть  – незамкнутая двусторонняя поверхность, ограниченная контуром 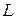, не имеющим точек самопересечения. Выберем определенную сторону поверхности заданием нормали. Будем называть положительным направлением обхода контура  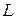то, при движении по которому по выбранной стороне поверхности сама поверхность остается слева. При этом нормаль к поверхности, отвечающая этой стороне направлена от ног к голове обходящего. Некоторые авторы учебников такое правило выбора положительного направления обхода называют «правилом штопора».

Аналогично устанавливается положительное направление обхода для любого замкнутого контура (без точек самопересечения), лежащего на поверхности . Направление обхода контура, противоположное положительному, называется отрицательным.

Определение. Двусторонняя поверхность с установленным на ней положительным направлением обхода контуров называется ориентированной поверхностью (рис. 3).

Если поверхность состоит из нескольких частей  (каждая из которых – двусторонняя поверхность), соединенных

Рис. 3 – Ориентированная поверхность            между собой по некоторым «ребрам», то в точках этих ребер касательная плоскость и нормаль к поверхности  может не существовать, то есть данное выше определение двусторонней поверхности к поверхности , вообще говоря, неприменимо. В этом случае можно соединить эти части в одну двустороннюю поверхность, согласовав ориентацию общих границ.

Замечание. Когда кусочно-гладкая поверхность ориентирована и замкнута, то, если не оговорено другого, всегда выбирается внешняя сторона поверхности, то есть в каждой точке выбирается вектор единичный нормали, направленный во внешность ограниченного данной поверхностью тела из .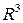

Так как сторона поверхности определяется заданием нормали, то покажем, как находится нормаль в случае явного и параметрического задания поверхности. Рассмотрим сначала поверхность , представляющую собой график функции , имеющей непрерывные частные производные для всех , где 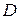 – область на плоскости .

У этой поверхности, очевидно, есть две стороны: верхняя и нижняя. Верхняя сторона может быть охарактеризована тем, что из двух возможных направлений нормали к этой поверхности в любой ее точке выбирается то, которое составляет с осью 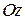 острый угол (нижней стороне, соответственно, отвечает тупой угол между нормалью и осью ).

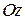Пусть  – точка этой поверхности, то есть .

Уравнение касательной плоскости к этой поверхности в точке  имеет вид .

Напомним, что в общем уравнении плоскости  числа  представляют собой координаты перпендикулярного к этой плоскости вектора. Тогда 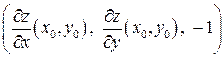 – координаты некоторого нормального вектора к поверхности в точке . Этот вектор, вообще говоря, не единичный. Умножая его на один из нормирующих множителей , мы получим два единичных вектора

, и .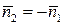

Известно, что координаты единичного вектора  – это косинусы углов, составляемых этим вектором с осями , соответственно, то есть , . Так как 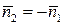, то , , . Кроме того, заметим, что , .

Отметим, что , поэтому верхней стороне соответствует вектор .

Рассмотрим случай, когда поверхность задаётся параметрическими уравнениями 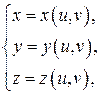 где  (  – некоторая область на плоскости ), а каждая точка поверхности получается лишь при одной паре значений параметров, так что параметрические уравнения устанавливают взаимно однозначное соответствие между точками поверхности  и точками плоской области . Такую поверхность будем называть простой. При этом предполагаем, что и область , и поверхность  ограничены простыми замкнутыми контурами, соответствующими друг другу при данном параметрическом задании. Параметры 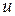 и  носят название криволинейных координат соответствующей точки. Если одну из координат зафиксировать, например , то, очевидно, получим уравнение некоторой кривой  принадлежащей поверхности . Меняя значения , получим целое семейство таких кривых, называемых координатными линиями. Аналогичное семейство кривых получается при фиксировании координаты . Если поверхность простая, то через любую её точку проходит по одной координатной линии из каждого семейства.

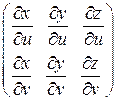Предположим теперь, что функции  не только непрерывны, но и имеют в области  непрерывные частные производные  (при выполнении этих условий мы говорим, что  – непрерывно дифференцируемые функции от ) и что в любой точке из области  ранг матрицы  равен 2. Это означает, что в любой точке  хотя бы один из миноров второго порядка этой матрицы не равен нулю. Пусть, например, . Тогда по теореме о разрешимости системы неявных функций в некоторой окрестности данной точки уравнения  можно решить и получить выражение 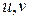 через 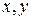, то есть  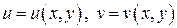(заметим, что эти функции непрерывно дифференцируемы). Тогда третье уравнение в окрестности рассматриваемой точки даст , то есть мы получаем явное уравнение вида .

Замечание. Если , то имеем, по аналогии, , а если , то .

Обозначим вектор = . Рассмотрим произвольную точку . Зафиксируем сначала  и рассмотрим  – кривую на поверхности 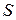. Тогда  – вектор касательной к этой кривой. Аналогично, 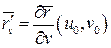 – вектор касательной к кривой .

Нормаль к поверхности является нормалью к касательной плоскости и перпендикулярна векторам  и . Условие  означает, что  и  не параллельны. Поэтому в качестве нормального вектора можно взять  (векторное произведение) или

.

Тогда единичные векторы нормали равны 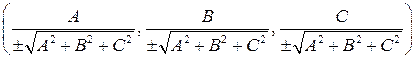, при этом выбору верхней нормали соответствует выбор того же знака, что и знак числа , перед корнем (поскольку тогда ).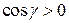

Площадь поверхности

Понятие площади кривой поверхности имеет аналогию с понятием длины кривой. Длину незамкнутой дуги мы определяли как предел периметра вписанной в дугу ломаной, при условии, что длины всех её сторон стремятся к нулю. В случае кривой поверхности естественно было бы рассматривать вписанную в неё многогранную поверхность и определять площадь кривой поверхности как предел площади этой многогранной поверхности, при условии, что диаметры всех граней стремятся к нулю. Но в конце 19 столетия Герман Амандус Шварц (1843 - 1921)  привёл пример поверхности, вписанной в прямой круговой цилиндр, для которой предел площади не существует (Пример Шварца смотри в Г.М.Фихтенгольц, Курс дифференциального и интегрального исчисления [1, т.3, стр. 249-250]).

Этот пример вынуждает нас иначе подойти к определению площади поверхности. Сначала определим это понятие для поверхности , заданной явным уравнением 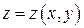, где  – непрерывная функция, обладающая непрерывными производными в некоторой квадрируемой (измеримой) области . Рассмотрим разбиение этой поверхности на части 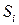 непрерывными кривыми. Под диаметром множества  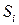понимается точная верхняя грань расстояний между точками этого множества. Диаметр всего разбиения – это наибольший из диаметров получившихся частей. Обозначают его .

В каждой полученной части поверхности выберем точку 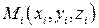 и рассмотрим касательную плоскость к поверхности в этой точке. Выбранные точки  породят набор касательных плоскостей, пересечения которых ограничат многоугольники, которые образуют «панцирь» на поверхности . Этот «панцирь» состоит из плоских многоугольников и, следовательно, имеет площадь, равную сумме площадей его многоугольников.

Если при стремлении к нулю диаметра разбиения площади «панцирей» имеют конечный предел, то он и называется площадью поверхности. Это определение позволяет легко найти формулу для вычисления площади поверхности. А именно, рассмотрим плоский многоугольник, нормаль к которому имеет направляющие косинусы . Можем считать, что .

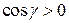Без ограничения общности, достаточно рассматривать прямоугольник, причем, для простоты, считаем, что его проекция на плоскость  есть прямоугольник со сторонами 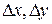, а сам он имеет стороны .

Тогда  и  ( 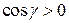). В общем случае .

Если нормали выбирались в точках 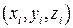, то пусть  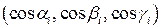– их направляющие косинусы. Согласно сказанному выше, площадь всего «панциря» есть .

Определение. Площадью элементарной гладкой поверхности с явным заданием называется конечный предел , если он существует (и как всегда при определении интегральных сумм, предел не должен зависеть от способа разбиения и от выбора точек). Поверхность в этом случае называется измеримой (квадрируемой), а площадь поверхности обозначается через .

Сумма  является интегральной суммой для двойного интеграла , поэтому

.

Замечание. Заметим, что если элементарная гладкая поверхность  с явным заданием лежит в координатной плоскости  (или любой другой), то, как следует из определения, она измерима (квадрируема) и её площадь – жорданова мера плоской области .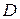

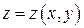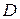Предположим теперь что поверхность, заданная параметрически, представляет собой конечное объединение частей, каждая из которых может быть задана явным уравнением. Рассмотрим одну из частей, для которой , . Площадь этой части, по доказанному выше, равна . Перейдем в этом интеграле к переменным , учитывая, что якобиан перехода – это как раз определитель , а , и пусть области  соответствует область  на плоскости 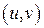. Тогда по теореме о замене переменных 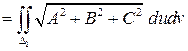. Легко проверить, что в случае уравнения  или  получится интеграл такого же вида: .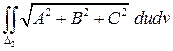

Объединяя все полученные части, получаем общую площадь , где  – вся область изменения параметров .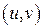

Отметим, что выражение  можно преобразовать к более удобному для вычислений виду. Числа  суть координаты вектора . Поэтому  – квадрат модуля вектора . Напомним, что модуль векторного произведения равен  (  – угол между  и ). Значит, .

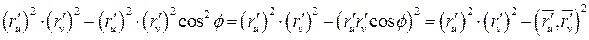Принято обозначать

;

;

.

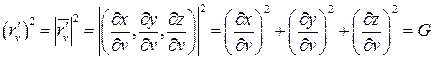Итак,

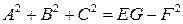
и формула для площади поверхности, заданной параметрически, такова: .

Пример. Вычислить площадь части гиперболического параболоида , вырезанной из него цилиндром .

Решение. Имеем поверхность , где . Поскольку функция  является непрерывно дифференцируемой в , то  – элементарная гладкая поверхность. Граница области 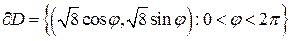 является окружностью (гладкой линией в ), поэтому 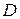 – измеримая по Жордану область.

Площадь указанной части гиперболического параболоида будет вычисляться по формуле

.

Переходя к полярным координатам, получим

.

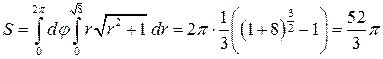Поверхностный интеграл по элементу поверхности (первого рода)

Поверхностный интеграл первого рода является таким же обобщением двойного интеграла, как криволинейный интеграл первого рода по отношению к определённому интегралу.

Задача о вычислении массы материальной поверхности. К понятию поверхностного интеграла приводит, например, задача вычисления массы, распределённой по поверхности  с переменной поверхностной плотностью 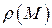. Для нахождения этой массы разбивают поверхность  на части 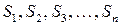 и выбирают в каждой из них по точке . Если эти части достаточно малы, то их массы приближённо равны , а масса всей поверхности будет приближённо равна . Это значение тем ближе к точному, чем меньше части 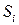. Поэтому точное значение массы поверхности есть

,

где предел берётся при условии, что размеры всех частей 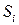 (и их площади 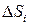) стремятся к нулю. К аналогичным пределам приводят и другие задачи физики.

А теперь сформулируем понятие поверхностного интеграла по элементу площади (первого рода).

Определение. Пусть  – измеримая двусторонняя поверхность в трёхмерном пространстве , имеющая площадь , а  – непрерывная функция, определённая в точках этой поверхности. Поверхность  с помощью непрерывных кривых, сетью линий разобьём на  участков , не имеющих общих внутренних точек (рис. 4).

Площади «элементарных» участков обозначим , , а наибольший из диаметров этих участков – через 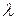. На каждом «элементарном» участке  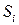произвольным образом выберем по точке . Значение функции  в точке  умножим

Рис. 4 – Построение интегральной суммы на площадь 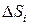 поверхности : , и сложим все полученные произведения.

Сумма

называется интегральной суммой для функции  по поверхности . Для данной функции  можно составить бесчисленное множество интегральных сумм по поверхности .

Определение. Если при стремлении к нулю шага разбиения 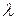 поверхности  существует конечный предел интегральных сумм , не зависящий от способа разбиения поверхности  на «элементарные» участки 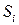 и от выбора точек , то он называется поверхностным интегралом первого рода от функции   по поверхности  и обозначается символом

.

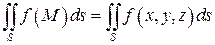Отметим, что в определении интеграла первого рода сторона поверхности не участвует. Пример задачи, моделью которой служит поверхностный интеграл первого рода – рассмотренная нами задача о нахождении массы поверхности , поверхностная плотность которой в точке  равна .

Приведём простейшие достаточные условия существования поверхностного интеграла первого рода.

Теорема. Пусть функция  непрерывна на ограниченной гладкой (или кусочно-гладкой) поверхности  с гладкой (или кусочно-гладкой) границей. Тогда поверхностный интеграл 1-го рода по этой поверхности существует.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться: