Сведение поверхностных интегралов первого рода к двойным

Вычисление поверхностных интегралов первого рода обычно производится путем их сведения к двойным интегралам.

Напомним формулировку теоремы о достаточных условиях существования поверхностного интеграла первого рода в случае явного задания поверхности.

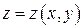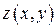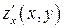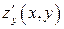Теорема. Если поверхность  задана уравнением , где функция  и её частные производные   и  непрерывны в замкнутой области  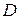(  – проекция поверхности  на координатную плоскость 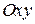), а функция  непрерывна на , то интеграл  существует.

К использованию этих условий сводится большинство практически встречающихся случаев. Для вычисления поверхностного интеграла 1-го типа удобно использовать следующие формулы.

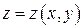Теорема 1. Пусть поверхность  задана явным уравнением , где  – непрерывно дифференцируемая на измеримой области  функция, . Тогда для любой непрерывной на поверхности  функции  выполнено .

Доказательство. Доказательство проведем конструктивным методом. Пусть функция  непрерывна на поверхности , заданной уравнением 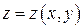, и удовлетворяет условиям приведённой выше теоремы существования поверхностного интеграла. Тогда для любого способа разбиения поверхности  на части и любого выбора точек  на этих частях всегда выполнено

.

Воспользуемся этим и построим интегральные суммы специальным образом. А именно, разобьем область 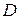 в плоскости  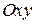на части , , …,  не имеющие общих внутренних точек. Обозначим через 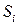 часть поверхности , проектирующуюся на плоскость 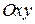 в область . При этом поверхность  окажется разбитой на 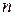 частей: , , 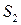…,  (рис. 5).

Площадь каждой части  может быть найдена по формуле

.

Применяя к двойному интегралу теорему о среднем, получим:

где  – некоторая точка области .

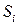А теперь обозначим через  точку поверхности  с координатами , где , и составим интегральную сумму для интеграла от функции  по поверхности ,

Рис. 5 – Поверхностный интеграл 1 рода соответствующую произведенному разбиению поверхности  на части и выбранным точкам , , на этих частях.

По доказанному

.

В правой части равенства имеем интегральную сумму для двойного интеграла от функции , непрерывной в области .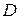

При стремлении к нулю шага разбиения области  шаг разбиения поверхности  (в силу непрерывности функций  и ) также стремится к нулю . В пределе получаем формулу

,

выражающую интеграл по поверхности  через двойной интеграл по проекции поверхности  на плоскость .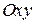

Аналогично получаются формулы, выражающие при соответствующих условиях интеграл по поверхности  через двойные интегралы по ее проекции на плоскости  и .

Замечание. Если поверхность задана уравнением , , где  - непрерывно дифференцируемая на измеримой области  функция, то .

Аналогично, в случае задания поверхности  уравнением  имеем

 при аналогичных условиях на область  и функцию .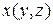

Теорема 2. Если поверхность  задана параметрическими уравнениями  где , а – непрерывно дифференцируемые функции на . Пусть  непрерывна на . Тогда .

Пример 1. Вычислим интеграл  по части поверхности конуса ,  (рис. 6).

Решение. Поверхность  проектируется на плоскость 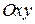 в область 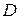, представляющую собой кольцо . В этом кольце функции , , 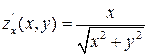 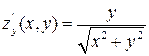Рис. 6 – Поверхность к примеру 1          непрерывны. Следовательно,

.

Пример 2. Найти , где  – винтовая поверхность .

Решение. Найдём коэффициенты : , , , , , , , , .

Вычислим поверхностный интеграл 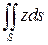, перейдя к двойному

.

С помощью поверхностных интегралов первого рода можно определять массы, статические моменты, моменты инерции, координаты центров тяжести и тому подобные величины для материальных поверхностей с известной плотностью распределения массы. Решение этих задач аналогично решению соответствующих задач для случая материальной кривой, материальной плоской и пространственной области.

Пример 3. Найти статический момент части цилиндра , лежащей между плоскостями  и , относительно плоскости , если поверхностная плотность .

Решение. Обозначим поверхность через , а искомый момент через . Параметризуем поверхность  при помощи уравнений .

Тогда , , ,

откуда .

Пример 4. Найти координаты центра тяжести массы однородной полусферы .

Решение. Обозначим полусферу через , плотность через , а искомые координаты центра тяжести через . Масса поверхности , очевидно, равна половине массы сферы . Из соображений симметрии . Введем параметризацию полусферы  с помощью сферических координат .

Тогда

, , .

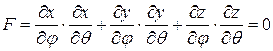Откуда .

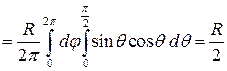Пример 5. Найти момент инерции однородного параболоида , , плотности  относительно оси .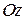

Решение. Обозначим параболоид через , момент через . Тогда .

Поверхностный интеграл по координатам (второго рода)

При введении понятия поверхностного интеграла 1 рода мы получали интегральные суммы, в которых значение функции в некоторой точке умножалось на площади элементов поверхности. В некоторых задачах физики, например при определении потока жидкости через поверхность , встречаются пределы аналогичных сумм с той лишь разницей, что вместо площадей самих частей стоят площади их проекций на три координатные плоскости. При этом поверхность  предполагается ориентированной (то есть указано, какое из направлений нормалей считается положительным) и площадь проекции берётся со знаком «+» или «–» в зависимости от того, является ли угол между положительным направлением нормали и осью, перпендикулярной плоскости проекций, острым или тупым.

Задача о вычислении количества жидкости, протекающей за единицу времени через заданную поверхность.

Поставим себе целью решить следующую задачу: сколько жидкости протечет через заданную поверхность за единицу времени, считая при этом, что плотность жидкости везде одна и та же («несжимаемая жидкость»); пусть для определенности она равна 1. Естественно, такая задача не может не привести к интегральной сумме и через нее – к интегралу. А именно, разбиваем поверхность , на кусочки, каждый из которых можно уже приближенно считать плоским, а поле  скоростей жидкости на протяжении этого кусочка постоянным. Рассмотрим один такой кусочек. За единицу времени частички жидкости, находившиеся в начальный момент на исследуемом кусочке, сместятся на отрезок, длина которого численно равна скорости (ведь скорость и есть «путь за единицу времени»). Как подсчитать объем вытекшего столбика жидкости? Естественно, нужно площадь основания умножить на высоту, которая равна «пути за единицу времени» только если скорость перпендикулярна площадке. А в общем случае нужно взять составляющую скорости, перпендикулярную к поверхности. Будем считать, что на нашей поверхности одна из сторон выделена; обычно это делают так: в какой-то точке поверхности строят вектор, перпендикулярный поверхности. Лучше всего считать, что этот вектор имеет некоторую заранее известную длину; чаще всего считают, что она равна 1. Когда мы передвигаемся по плоскости, вместе с нами передвигается и вектор нормали. Та сторона, на которой стоит вектор, и считается выделенной. Если же мы встретили поверхность одностороннюю, то с помощью задания нормали выделить сторону поверхности невозможно. Что же в этом случае делать? Я вижу тут следующий выход: считать, что суммарно жидкость через нее протекла в нулевом количестве (в смысле: сколько втекло, столько и вытекло). В самом деле, тот наблюдатель, который (условно) стоит вверх головой, подсчитывает количество протекающей жидкости через ту или иную площадку, ориентируясь на свою нормаль, а тот наблюдатель, который вслед за Мебиусом ушел туда, откуда Мебиус слышал лай своей собаки, доносящийся как бы из-под земли, также подсчитывает количество протекающей жидкости, но если, скажем, первому кажется, что это количество нужно учитывать со знаком плюс, так как жидкость вырывается из поверхности в виде гейзера, то второму кажется, что идет дождик.

Заканчиваем рассуждение про вычисление количества жидкости за единицу времени. Конечно, мы должны просуммировать результаты, полученные для каждой площадки и перейти к пределу.

Перейдём к построению поверхностного интеграла второго рода. Как при изучении криволинейных интегралов второго рода рассматривалась направленная кривая, так и при построении поверхностного интеграла второго рода рассматривается определенная сторона поверхности.

Определение. Возьмём в пространстве  двустороннюю поверхность , состоящую из конечного числа кусков, каждый из которых задан уравнением вида   или является цилиндрической поверхностью с образующими, параллельными оси .

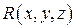Пусть  – функция, определенная и непрерывная на поверхности . Выберем определенную сторону поверхности . Сетью линий разбиваем  произвольным образом на  «элементарных» участков , не имеющих общих внутренних точек (рис. 7).

На каждом участке  произвольным образом выберем точку . Пусть  – площадь проекции участка 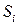 на координатную плоскость 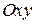, взятая со знаком «+», если нормаль к

Рис. 7 – Поверхностный интеграл 2 рода поверхности  в точке 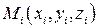 образует с осью  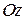острый угол, и со знаком «‑ », если этот угол тупой.

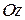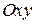Если поверхность деления лежит на, цилиндрическом куске поверхности  с образующими, параллельными оси , то проекция  на плоскость  представляет собой дугу кривой, так что вопрос о знаке  в этом случае отпадает,  (рис. 8).

Возьмем на каждой части  поверхности  произвольно точку  и умножим значение

Рис. 8 – Цилиндрическая поверхность       функции 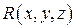 в точке  на :

.

Сумма всех таких произведений

называется интегральной суммой для функции 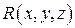 по поверхности  по переменным  и . Естественно, что таких сумм для заданной на поверхности  функции  можно составить бесчисленное множество.

Обозначим через  – наибольший из диаметров 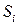, . Если при стремлении к нулю шага разбиения  поверхности  интегральные суммы имеют конечный предел

,

не зависящий от способа разбиения поверхности  на «элементарные» участки  и не зависящий от выбора точек , , то он называется поверхностным интегралом по выбранной стороне поверхности   от функции   по координатам ,   (или поверхностным интегралом второго рода) и обозначается

.

Так как этот символ не содержит указания на сторону поверхности , ее приходится задавать дополнительно.

Аналогично можно построить поверхностные интегралы по выбранной стороне поверхности 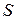 по координатам ,  или ,  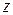по соответствующей стороне поверхности, от функции  ( ), определенной на поверхности : то есть

, .

Здесь  площадь проекции поверхности  на плоскость .

Если существуют интегралы ,  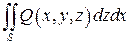и , то можно ввести поверхностный интеграл «общего» вида по выбранной стороне поверхности:

.

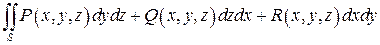Замечание. При построении интегральных сумм в начале параграфа мы умножали значение функции на значение площадей проекции поверхности, знак которых зависел от выбранного направления нормали, а поэтому интегральные суммы будут менять знак на противоположный при выборе иного направления нормали. А это значит, что в отличие от поверхностного интеграла первого рода, знак поверхностный интеграл второго рода зависит от ориентации поверхности .

Достаточные условия существования поверхностного интеграла второго рода аналогичны условиям существования поверхностного интеграла первого рода.

Теорема. Пусть функция  непрерывна на ограниченной гладкой (или кусочно-гладкой) поверхности 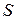 с гладкой (или кусочно-гладкой) границей. Тогда поверхностный интеграл  по этой поверхности существует.

⇐ Предыдущая123456Следующая ⇒

Поделиться: