Сведение поверхностных интегралов второго рода к двойным
По аналогии с поверхностными интегралами первого рода вычисление поверхностных интегралов второго рода, как правило, сводят к вычислению двойного интеграла.
Теорема. Пусть поверхность 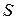 задана уравнением
задана уравнением 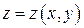 , где
, где 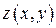 – непрерывно дифференцируемая в области
– непрерывно дифференцируемая в области 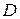 функция,
функция, 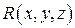 – непрерывная на
– непрерывная на 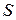 функция. Тогда если выбрана верхняя сторона
функция. Тогда если выбрана верхняя сторона 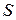 , то
, то 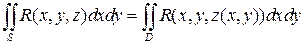 , а если выбрана нижняя сторона, то
, а если выбрана нижняя сторона, то 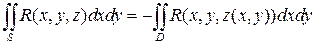 .
.
Замечание. Интегрирование по нижней стороне поверхности 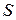 сводится к интегрированию по верхней стороне после перемены знака перед интегралом.
сводится к интегрированию по верхней стороне после перемены знака перед интегралом.
Следствие 1. Аналогичным образом устанавливается справедливость формул:
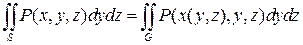
для функции 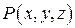 , непрерывной на двухсторонней поверхности
, непрерывной на двухсторонней поверхности 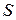 , заданной уравнением
, заданной уравнением 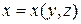 (
( 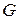 – проекция поверхности
– проекция поверхности  на плоскость
на плоскость 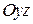 ), если выбранная нормаль к поверхности
), если выбранная нормаль к поверхности  составляет с осью
составляет с осью 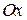 острый угол, и
острый угол, и
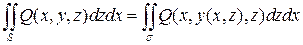
для функции 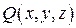 , непрерывной на двухсторонней поверхности
, непрерывной на двухсторонней поверхности 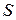 , заданной уравнением
, заданной уравнением 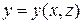 (
( 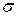 – проекция поверхности
– проекция поверхности  на плоскость
на плоскость 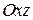 ), если выбранная нормаль к поверхности
), если выбранная нормаль к поверхности  составляет с осью
составляет с осью 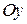 острый угол.
острый угол.
Следствие 2. Если двухстороннюю поверхность  можно разбить на конечное число кусков, каждый из которых либо задается уравнением вида
можно разбить на конечное число кусков, каждый из которых либо задается уравнением вида 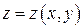 , где
, где 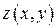 – функция, непрерывная в замкнутой измеримой (квадрируемой) области – проекции соответствующего куска поверхности
– функция, непрерывная в замкнутой измеримой (квадрируемой) области – проекции соответствующего куска поверхности  на плоскость
на плоскость  , либо является цилиндрической поверхностью с образующими, параллельными оси
, либо является цилиндрической поверхностью с образующими, параллельными оси  , то интеграл по выбранной (любой) стороне поверхности
, то интеграл по выбранной (любой) стороне поверхности  от непрерывной на поверхности функции
от непрерывной на поверхности функции 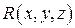
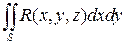
существует и равен алгебраической сумме двойных интегралов по проекциям указанных кусков поверхности  вида
вида 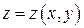 на плоскость
на плоскость 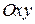 .
.
Аналогичные утверждения имеют место для интегралов вида
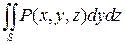 и
и 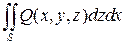 .
.
Следствие 3. В случае если поверхность  может быть задана уравнением
может быть задана уравнением  , где функция
, где функция 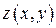 и ее частные производные
и ее частные производные 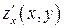 и
и 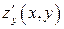 непрерывны в замкнутой измеримой (квадрируемой) области
непрерывны в замкнутой измеримой (квадрируемой) области 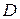 – проекции поверхности
– проекции поверхности  на плоскость
на плоскость 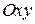 , а функции
, а функции 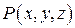 ,
, 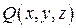 и
и 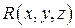 непрерывны на поверхности
непрерывны на поверхности  , имеет место следующая формула:
, имеет место следующая формула:
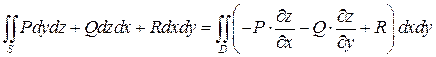 ,
,
выражающая поверхностный интеграл общего вида по верхней стороне поверхности  через двойной интеграл по проекции поверхности
через двойной интеграл по проекции поверхности  на плоскость
на плоскость 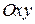 .
.
Следствие 4. Если поверхность  допускает представление как в виде
допускает представление как в виде  ,
, 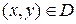 , так и в виде
, так и в виде 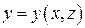 ,
, 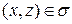 , и в виде
, и в виде 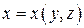 ,
, 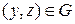 , то при выполнении условий теоремы справедливо равенство
, то при выполнении условий теоремы справедливо равенство
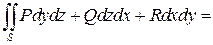
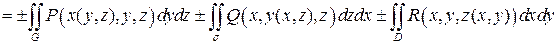 ,
,
где выбор знака «+» или «–» перед соответствующим слагаемым в правой части равенства определяется тем, какой угол составляют нормали к выбранной стороне с соответствующей осью.
Связь между поверхностными интегралами первого и второго рода
Пусть поверхность  задана уравнением:
задана уравнением: 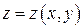 , причем
, причем 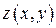 ,
, 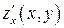 ,
, 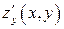 – непрерывные функции в замкнутой области
– непрерывные функции в замкнутой области 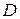 (проекции поверхности
(проекции поверхности 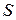 на координатную плоскость
на координатную плоскость 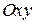 ), а функция
), а функция 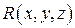 непрерывна на поверхности
непрерывна на поверхности 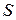 . Тогда
. Тогда
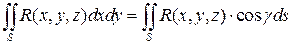 .
.
Для общего случая имеем:
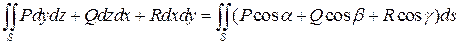 ,
,
где 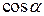 ,
, 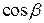 ,
, 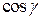 – направляющие косинусы нормали к поверхности
– направляющие косинусы нормали к поверхности 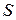 для выбранной (в интеграле слева) стороны поверхности.
для выбранной (в интеграле слева) стороны поверхности.
Дополнительно сформулируем правило вычисления поверхностного интеграла в случае параметрического задания поверхности.
Теорема 2. Пусть двусторонняя поверхность  задана параметрическими уравнениями
задана параметрическими уравнениями 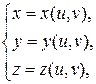
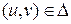 , где
, где 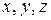 – непрерывно дифференцируемые функции и ранг матрицы
– непрерывно дифференцируемые функции и ранг матрицы 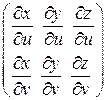 равен двум. Тогда, для непрерывных на
равен двум. Тогда, для непрерывных на  функций
функций 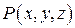 ,
, 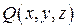 ,
, 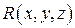 , и выбранной нормали (
, и выбранной нормали ( 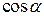 ,
, 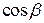 ,
, 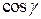 ), выполнено
), выполнено
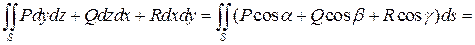
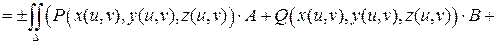
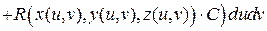 ,
,
где, напоминаем, 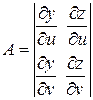 ,
, 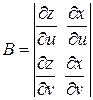 ,
, 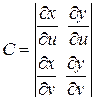 . При этом выбор знака «+» или «‑ » перед интегралом производится в соответствии с выбором нормали (и, следовательно, стороны) поверхности. К примеру, если указано, что нормаль составляет с осью
. При этом выбор знака «+» или «‑ » перед интегралом производится в соответствии с выбором нормали (и, следовательно, стороны) поверхности. К примеру, если указано, что нормаль составляет с осью  острый угол, то знак перед интегралом совпадает со знаком определителя
острый угол, то знак перед интегралом совпадает со знаком определителя 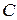 .
.
Пример 1. Вычислить 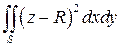 по верхней стороне полусферы
по верхней стороне полусферы 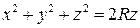 ,
, 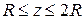 (рис. 9).
(рис. 9).
Решение. Очевидно, что уравнение сферы можно записать: 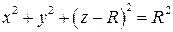 . Отсюда уравнение полусферы при
. Отсюда уравнение полусферы при 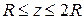 имеет вид:
имеет вид: 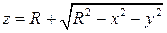 .
.
Рис. 9 – Полусфера Поскольку нормаль 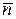 к верхней стороне полусферы составляет с осью
к верхней стороне полусферы составляет с осью  острый угол, то элементы
острый угол, то элементы  нужно брать со знаком «+», то есть имеем:
нужно брать со знаком «+», то есть имеем:
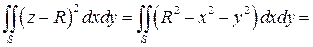
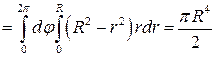 .
.
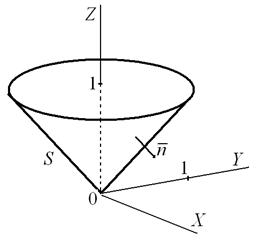
Пример 2. Вычислить 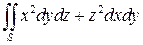 по нижней стороне конуса
по нижней стороне конуса 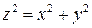 ,
, 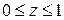 (рис. 10).
(рис. 10).
Решение 1. Вычислим отдельно интегралы от каждого из слагаемых, используя явное задание поверхности:
Рис. 10 – Конус 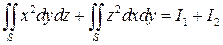 .
.
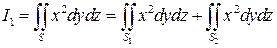 , где
, где 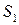 , это
, это 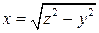 , а
, а 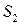 , это
, это 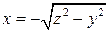 . При этом нормаль к поверхности
. При этом нормаль к поверхности 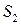 составляет тупой угол с осью
составляет тупой угол с осью 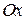 , значит перед вторым интегралом нужно изменить знак. Заметим, что проекцией
, значит перед вторым интегралом нужно изменить знак. Заметим, что проекцией 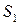 и
и 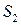 на плоскость
на плоскость 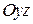 будет треугольник
будет треугольник 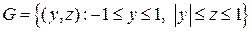 .
.
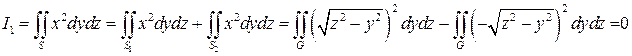 .
.
Перейдем к вычислению интеграла от второго слагаемого 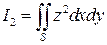 . Нормаль к поверхности
. Нормаль к поверхности  составляет тупой угол с осью
составляет тупой угол с осью  , значит перед интегралом нужно изменить знак. Проекцией поверхности
, значит перед интегралом нужно изменить знак. Проекцией поверхности  на плоскость
на плоскость 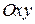 будет круг
будет круг 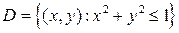 . Прейдём к полярным координатам
. Прейдём к полярным координатам
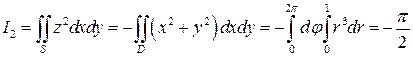 .
.
Следовательно: 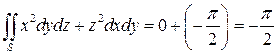 .
.
Решение 2. Приведём иное решение второго примера, используя параметрическое задание поверхности  :
:
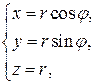
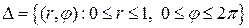 . Определители,
. Определители, 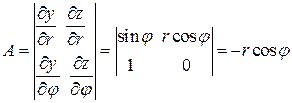 ,
,  . Нормаль к поверхности
. Нормаль к поверхности  составляет тупой угол с осью
составляет тупой угол с осью  , следовательно, определитель
, следовательно, определитель 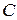 должен принимать отрицательные значения, а поэтому перед интегралом нужно поменять знак на противоположный. Имеем
должен принимать отрицательные значения, а поэтому перед интегралом нужно поменять знак на противоположный. Имеем
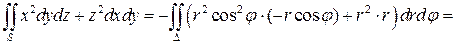
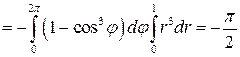 .
.
Формула Стокса
Формула Стокса устанавливает связь между криволинейным и поверхностным интегралами второго рода.
Теорема. Пусть  – гладкая ориентированная двусторонняя поверхность (то есть направление нормали выбрано) и
– гладкая ориентированная двусторонняя поверхность (то есть направление нормали выбрано) и 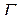 – кусочно-гладкая кривая, ограничивающая
– кусочно-гладкая кривая, ограничивающая  , причем мы считаем направление обхода
, причем мы считаем направление обхода 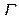 положительным. Пусть функции
положительным. Пусть функции 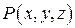 ,
, 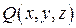 ,
, 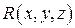 – непрерывно дифференцируемые. Тогда имеет место формула Стокса
– непрерывно дифференцируемые. Тогда имеет место формула Стокса
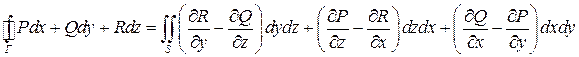 .
.
Доказательство. Предположим, что наша поверхность  задаётся параметрически
задаётся параметрически 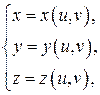 где
где 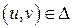 (
( 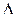 – некоторая область на плоскости
– некоторая область на плоскости 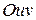 ). Тогда для кривой
). Тогда для кривой 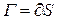 параметризация примет вид
параметризация примет вид 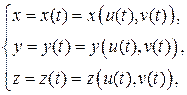
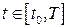 , где
, где 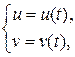
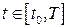 параметризация проекции
параметризация проекции 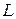 кривой
кривой 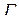 на плоскость
на плоскость 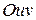 : (разумеется, здесь
: (разумеется, здесь  – непрерывно дифференцируемые функции).
– непрерывно дифференцируемые функции).
Вычислим, например, 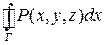 . Перейдём от криволинейного интеграла к определённому
. Перейдём от криволинейного интеграла к определённому
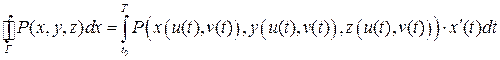 .
.
Так как  сложная функция, то
сложная функция, то 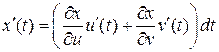 и наш интеграл примет вид
и наш интеграл примет вид
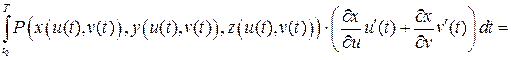
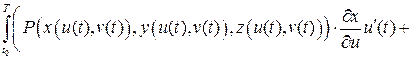
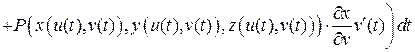 .
.
Но 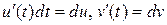 . Тогда, с учётом параметризации кривой
. Тогда, с учётом параметризации кривой 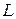 наш определённый интеграл равен криволинейному по плоской кривой
наш определённый интеграл равен криволинейному по плоской кривой 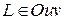
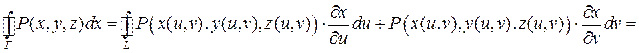
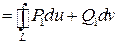 .
.
Мы перешли от интеграла по пространственной дуге 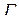 к интегралу по плоской дуге
к интегралу по плоской дуге 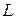 . Так как
. Так как 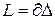 , то к плоской кривой
, то к плоской кривой 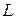 применим формулу Грина:
применим формулу Грина: 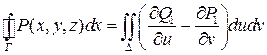 .
.
Рассмотрим подынтегральное выражение
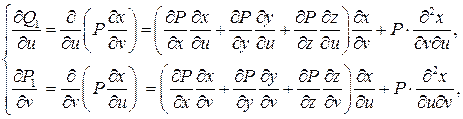
Так как вторые смешанные производные функции 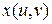 непрерывны, то последние слагаемые сократятся. Имеем
непрерывны, то последние слагаемые сократятся. Имеем
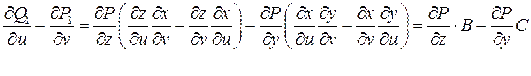 ,
,
и мы приходим к двойному интегралу
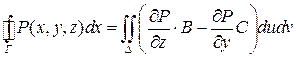 .
.
Осталось воспользоваться формулой
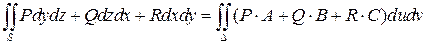
из теоремы 2 на 34 странице, а именно 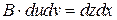 ,
, 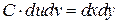 :
:
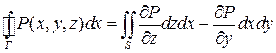 .
.
При этом выбор стороны поверхности 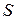 согласован с направлением обхода контура
согласован с направлением обхода контура 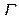 , так как именно эту сторону характеризует выбор знака определителей
, так как именно эту сторону характеризует выбор знака определителей 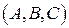 .
.
При помощи круговой перестановки переменных 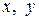 и
и  получаются аналогичные равенства для функций
получаются аналогичные равенства для функций 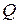 и
и 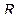 , удовлетворяющим тем же условиям что и
, удовлетворяющим тем же условиям что и 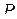 :
:
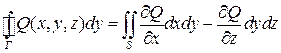 ,
,
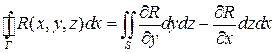 .
.
Сложим полученные равенства
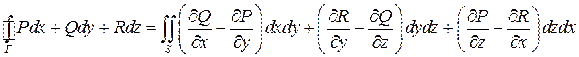 .
.
Формула Стокса доказана.
Замечание 1. При замене поверхностного интеграла второго рода на поверхностный интеграл первого рода получим равносильную формулировку:
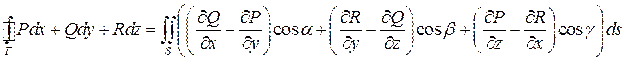 .
.
Замечание 2. В случае кривой  , лежащей в плоскости
, лежащей в плоскости  и функций
и функций 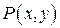 ,
, 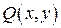 , удовлетворяющих условиям теоремы, формула Стокса совпадает с формулой Грина.
, удовлетворяющих условиям теоремы, формула Стокса совпадает с формулой Грина.
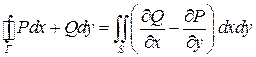 .
.
Следовательно, формула Грина является частным случаем формулы Стокса.
Замечание 3. Формулы в правой части запомнить непросто. Поэтому удобно записать подынтегральное выражение в виде определителя
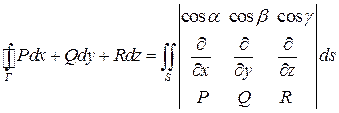 .
.
Разумеется, это не совсем обычный определитель. Ведь во второй строке его стоят операторы дифференцирования. Поэтому условимся считать, что мы понимаем под этим определителем его формальное разложение по первой строке, причем произведение, например, оператора 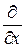 на функцию
на функцию 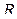 есть
есть 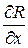 и т.п. То есть формула Стокса устанавливает связь между интегралом по поверхности и криволинейным интегралом по контуру, ограничивающему эту поверхность.
и т.п. То есть формула Стокса устанавливает связь между интегралом по поверхности и криволинейным интегралом по контуру, ограничивающему эту поверхность.
Формула Стокса выражает криволинейный интеграл по контуру 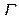 через интеграл по поверхности
через интеграл по поверхности 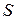 , «натянутой» на этот контур. Сторона поверхности и направление обхода контура
, «натянутой» на этот контур. Сторона поверхности и направление обхода контура 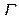 взаимно определяют друг друга. Вообще говоря, формула Стокса имеет место для любой незамкнутой, ограниченной контуром
взаимно определяют друг друга. Вообще говоря, формула Стокса имеет место для любой незамкнутой, ограниченной контуром  поверхности
поверхности 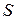 , состоящей из конечного числа поверхностей рассмотренного вида, а также для поверхностей, обладающих указанными свойствами, относительно других координатных плоскостей.
, состоящей из конечного числа поверхностей рассмотренного вида, а также для поверхностей, обладающих указанными свойствами, относительно других координатных плоскостей.
Воспользуемся формулой Стокса для переноса на пространственные криволинейные интегралы (поверхностные интегралы) результатов об условиях независимости криволинейного интеграла от кривой интегрирования, полученных для плоского случая с помощью формулы Грина (12 теорем).
Определение 2. (Аналогичное определению односвязности плоской области) Область 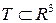 называется поверхностно односвязной, если для любой замкнутой кусочно-гладкой линии
называется поверхностно односвязной, если для любой замкнутой кусочно-гладкой линии 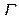 , лежащей в
, лежащей в 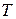 , найдется кусочно-гладкая поверхность
, найдется кусочно-гладкая поверхность 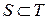 , границей которой является
, границей которой является 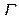 .
.
Примерами поверхностно односвязных областей являются шар, область, заключенная между двумя концентрическими сферами, пространство 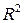 . Примером области, которая не является поверхностно односвязной, является тор.
. Примером области, которая не является поверхностно односвязной, является тор.
Сформулируем теорему об эквивалентности четырех утверждений, аналогичную теореме для приложения теоремы Грина при изучении криволинейных интегралов.
Теорема (12 теорем). Пусть функции 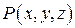 ,
, 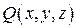 ,
, 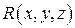 – непрерывно дифференцируемы в поверхностно односвязной области
– непрерывно дифференцируемы в поверхностно односвязной области 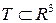 . Тогда следующие утверждения равносильны:
. Тогда следующие утверждения равносильны:
I Выполняются равенства: 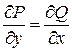 ,
, 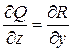 ,
, 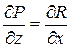 в
в 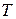 .
.
II Для любой замкнутой кусочно-гладкой кривой 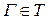
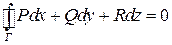 .
.
III Для любых двух точек 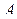 и
и 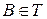 значение интеграла
значение интеграла 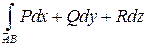 , не зависит от выбора кусочно-гладкой кривой
, не зависит от выбора кусочно-гладкой кривой 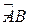 , соединяющей точки
, соединяющей точки 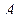 и
и 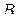 в
в 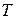 .
.
 IV Выражение
IV Выражение 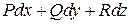 является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 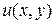 , определенной в
, определенной в 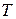 и такой, что
и такой, что 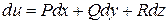 .
.
В этом случае  для любой кривой
для любой кривой 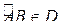 .
.
Пример. Вычислить 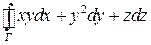 вдоль линии
вдоль линии 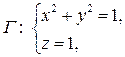 ограничивающей поверхность Рис. 11 – Параболоид
ограничивающей поверхность Рис. 11 – Параболоид 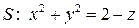 (рис. 11).
(рис. 11).
Решение. Проекцией поверхности 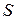 на плоскость
на плоскость  будет круг
будет круг 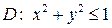 . Воспользовавшись формулой Стокса, получаем:
. Воспользовавшись формулой Стокса, получаем:
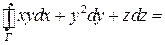
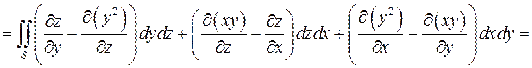
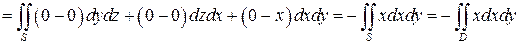 .
.
Переходя к полярным координатам, получим
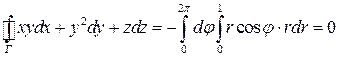 .
.

