Вивчення вимушених коливань. ⇐ ПредыдущаяСтр 13 из 21Следующая ⇒ Підняти вгору переривач (9) світлового потоку на стержні маятника (7), а переривач світлового потоку (12) на (8) опустити вниз навпроти фотоелектричного датчика (14). Привести в дію електродвигун, визначити частоту коливань шатуна і максимальну амплітуду вимушених коливань маятника (7). Вимірювання провести при різних частотах коливань до і після досягнення резонансу. Результати вимірювань записати в таблицю і зобразити графічно, відкладаючи на осі абсцис циклічну частоту шатуна, а на осі ординат – амплітуди коливань маятника. Визначити з графіку резонансну частоту.     ЧАСТИНА 3. МОЛЕКУЛЯРНА ФІЗИКА Лабораторна робота № 2.01. Визначення динамічної в’язкості рідини Вступ В рідині або в газі, у яких різні шари рухаються з неоднаковими швидкостями, виникають сили внутрішнього тертя, або так звані сили в’язкості. Дослідним шляхом встановлено, що сили внутрішнього тертя пропорційні градієнту швидкості шарів і площі поверхні дотичних шарів , що рухаються паралельно:                                     ,                                  (1) де  – градієнт швидкості, тобто величина, рівна зміні швидкості шарів на одиницю довжини в напрямку, перпендикулярному до напряму переміщення шарів (рис. 2.1). Рис. 2.1

Коефіцієнт пропорційності  називається динамічною в’язкістю. Чисельно він дорівнює силі внутрішнього тертя, що діє на одиницю площі шару при градієнті швидкості, рівному одиниці.

Згідно молекулярно-кінетичної теорії явище внутрішнього тертя пояснюється тим, що між шарами рідини або газу відбувається обмін впорядкованого руху.

В кожному з шарів молекули рухаються з однаковою швидкістю шару і в той же час здійснюють хаотичний тепловий рух всередині шару, внаслідок якого і здійснюється їх перехід з одного шару в інший. Внаслідок хаотичності теплового руху число молекул , що проходить за одиницю часу з шару 1 в шар 2 і навпаки (рис. 2.1) однакове, але вони переносять різні імпульси  і . Різниця  представляє собою зміну імпульсу шару 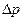 за одиницю часу. Згідно з основним рівнянням динаміки зміна імпульсу за одиницю часу рівна діючій силі , яка і представляє собою силу внутрішнього тертя. Існують різні методи визначення динамічної в’язкості рідин. В цій роботі використовуються два методи.

Метод Стокса

Цей метод основується на вимірюванні швидкості рівномірного падіння кульки в досліджуваній рідині.

На кульку радіуса , що падає у в’язкій рідині, діє три сили:

1. Сила тяжіння

                               ,                             (2)

де  – густина матеріалу кульки;

2. Виштовхувальна сила (сила Архімеда);

                                 ,                               (3)

де 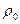 – густина рідини. Знак “мінус” означає що ця сила напрямлена в сторону, протилежну силі тяжіння ;

3. Сила опору рідкого середовища, обумовлена силами внутрішнього тертя рідини. Згідно з формулою, виведеною Стоксом на основі співвідношення (1), ця сила дорівнює:

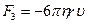                                    ,                                 (4)

де 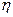 – динамічна в’язкість рідини,  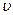– швидкість кульки. Знак “мінус” показує, що сила опору середовища має напрямок, протилежний швидкості .

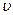Формула (3) застосовується до твердої кульки, оточеної однорідною рідиною, якщо швидкість кульки невелика і віддаль від кульки до границі рідини значно більша, ніж її діаметр. Слід підкреслити, що у виникненні сили опору має значення не тертя кульки з рідиною, а сили тертя між шарами рідини, що захоплюються кулькою. Найближчий до поверхні кульки шар рідини рухається з швидкістю кульки. Швидкість решти шарів зменшується по мірі віддалення їх від кульки і на деякій віддалі від його поверхні дорівнює нулю.

Рівнодійна всіх сил дорівнює:

                          (5)

Спочатку, поки швидкість кульки невелика, вона буде падати прискорено. Але з збільшенням швидкості кульки зростає, як видно з формули (3), сила опору 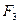, в той час як сили  і  залишаються постійними. Тому через деякий час кулька досягає такої швидкості , при якій всі сили будуть в сумі дорівнювати нулю:

                                            (6)

тобто рух кульки буде рівномірним.

З формули(6) слідує:

                                                             (7)

Знаючи 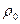, , , визначивши швидкість рівномірного руху кульки, можна за формулою (7) знайти динамічну в’язкість.

Пристрій, на якому проводять вимірювання, представляє собою циліндричну скляну посудину (рис. 2.2), наповнену досліджуваною рідиною, на якій є дві горизонтальні мітки N і M. Верхня мітка знаходиться нижче рівня рідини в тому самому місці, починаючи від якого рух кульки стає рівномірним. Діаметри кульок вимірюються мікрометром або за допомогою мікроскопа з окулярним мікрометром.

Завдання

1. Виміряти віддалі між мітками масштабною лінійкою.

2. Виміряти взаємно перпендикулярні діаметри кульки і визначити середнє з обох значень.

3. За допомогою пінцету помістити кульку над серединою поверхні рідини і, спостерігаючи за її падінням, виміряти секундоміром час, за який кулька проходить віддаль між мітками. Слід звернути увагу на те, щоб при пуску і зупинці секундоміра око було розташоване на рівні відповідної мітки.

Рис. 2.2

4. Провести вимірювання діаметра і часу падіння для кількох (не менше 5-и) кульок, виготовлених з одного матеріалу.

5. Для кожної кульки по формулі (7) визначити  – динамічну в’язкість, використовуючи табличні значення  і .

6. Оцінити похибки визначення .

7. Аналогічно провести вимірювання динамічної в’язкості, використовуючи інший набір кульок, що відрізняється від попереднього тільки розмірами, а також набір кульок того ж розміру, що і перший, але виготовлених з іншого матеріалу.

8. Порівняти середні значення коефіцієнта , одержані при використанні трьох комплектів кульок, з табличним його значенням для даної температури. Проаналізувати результати експерименту.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться: