Вказівки до виконання роботи ⇐ ПредыдущаяСтр 8 из 21Следующая ⇒ 1. Спрямувати пучок світла на нульову відмітку шкали слід шляхом повороту дзеркала довкола осі вертикального стержня і переміщення вздовж стержня, притримуючи при цьому мішень так, щоб її площина була перпендикулярна до горизонтальної осі „пістолета”. Якщо потім відпустити мішень, то хрестовина починає здійснювати невеликі коливання довкола вертикальної осі, і „зайчик” світлового променя переміщається по шкалі вліво і вправо від нульової відмітки. Слід домогтися припинення цих коливань, обережно повертаючи гайку В до тих пір, поки коливання хрестовини не припиняться. 2. Кожний з періодів  і  необхідно визначити з 3-5 дослідів. Контрольні запитання 1. Якими величинами визначається період коливань крутильного маятника? 2. З якою метою визначається два періоди коливань маятника  і ? 3. Який аналітичний вигляд мають закони збереження моменту імпульсу і енергії в даній роботі?   Лабораторна робота № 1.04. Визначення модуля зсуву методом крутильних коливань Вступ Модуль зсуву є однією з характерних пружних властивостей деформованих твердих тіл. Деформація тіла, тобто зміна його форми і розмірів, відбувається під дією прикладеної до неї зовнішньої сили. Якщо після припинення дії зовнішньої сили тіло приймає початкові розміри і форму, то така деформація називається пружною, а виникаючі між різними частинами деформованого тіла внутрішні сили – пружними силами. Для кожного реального тіла існує своя границя пружності, тобто та допустима гранична величина деформації, після припинення дії якої тіло, завдяки дії пружних сил, відновлює свої розміри і форму. При деформаціях вище границі пружності зміни форми тіла стають необоротними. Така деформація називається пластичною (залишковою). Рис. 1.5

Основними типами деформацій є деформації розтягу (стиску) і зсуву, так як деформацію любого іншого виду можна представити у вигляді суми цих двох деформацій. Зсувом називається така деформація тіла, при якій всі її плоскі шари, паралельні до площини, вздовж якої діє прикладена до тіла деформуюча сила 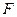, зсунуті один відносно одного так, як показано на (рис. 1.5).

Величина деформації зсуву характеризується тангенсом кута зсуву, який називається відносним зсувом. При пружних деформаціях кут  дуже малий, тому можна прийняти, що . Дія деформуючої сили зрівноважується виникаючою в тілі пружною силою. Величина, що дорівнює відношенню пружної сили 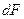 до площі поверхні , на яку вона діє, називається напруженням. Якщо пружна сила направлена по дотичній до поверхні, то напруження називається тангенціальним і позначається . Внаслідок взаємодії частин тіла одна з одною напруження передається у всі точки тіла так, що в любому перерізі, паралельному до площини, вздовж якої діє прикладена до тіла деформуюча сила, виникає тангенціальне напруження

                                       .                                    (1).

При невеликих значеннях тангенціального напруження залежність між  і  можна представити законом прямої пропорційності (закон Гука):

                                      ,                                    (2)

де  – постійний для даного матеріалу і залежний тільки від його властивостей коефіцієнт пропорційності, який називається модулем зсуву. Він дорівнює такому тангенціальному напруженню, при якому кут зсуву  дорівнював би 45° , якби при таких великих деформаціях не була перевищена границя пружності і зберігалась прямо пропорційна залежність між  і . Модуль зсуву має розмірність напруження і вимірюється в Паскалях (Па), т. я.  безрозмірна величина.

Метод вимірювання

В даній роботі метод визначення модуля зсуву оснований на вимірюваннях періоду коливань крутильного маятника, що складається з закріпленого в кронштейні зразка у вигляді циліндричного стержня, до якого закріплена горизонтальна хрестовина, навантажена чотирма однаковими вантажами (рис. 1.6). Крутильні коливання хрестовин здійснюються довкола вертикальної осі під дією моменту пружних сил, що виникає при закручуванні стержня на кут . Цей момент при малих кутах кручення, згідно з законом Гука, пропорційний величині кута

          ,                 (3)

де  – коефіцієнт пропорційності, що залежить від розмірів і пружних властивостей матеріалу стержня і називається модуль кручення.

Рис. 1.6

       При деформації кручення незакріплений переріз стержня під дією моменту зовнішніх сил повертається довкола осі стержня на кут , внаслідок чого твірні циліндричної поверхні зсуваються на кут  (рис. 1.7), при чому . Отже, в процесі закручування стержень зазнає деформації зсуву. Тому деформацію кручення можна представити як суму деформації зсуву і виразити модуль кручення стержня через модуль зсуву:

                                      ,                                   (4)

 де 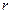 – радіус стержня,  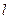– його довжина. З цього виразу можна знайти модуль зсуву , якщо відомо коефіцієнт жорсткості стержня . Коефіцієнт жорсткості визначається через період коливань крутильного маятника, який, як показано в роботі №1.03, дорівнює:

                                     ,                                  (5)

де  – момент інерції відносно осі обертання. Для визначення модуля кручення  необхідно з виразу (5) виключити момент інерції. Для цього вимірюється два періоди коливань маятника, що відповідають двом положенням вантажів на хрестовині, тобто двом моментам інерції:

                        ; ;                     (6)

Моменти інерції крутильного маятника  і  можна представити як суму моментів інерції хрестовини разом із стержнем  і момент інерції вантажів відносно осі обертання

                    , ,                 (7)

де  – маса одного вантажу,  і  – віддаль від осі обертання до центру вантажів. З виразу (6) і (7) маємо:

.                    (8)

З системи двох рівнянь знайдемо модуль кручення і, відповідно до формули (4), модуль зсуву:

           ,               (9)

Рис. 1.7

Завдання

1. Встановити всі чотири вантажі на віддалі 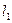, від осі стержня. Привести маятник в коливний рух, для чого повернути хрестовину довкола вертикальної осі на невеликий кут (не більше 10°) і залишити їй свободу руху. За допомогою секундоміру виміряти час двадцяти коливань і вирахувати період коливань . Вимірювання провести не менше 5-ти разів і знайти середнє значення періоду .

2. Аналогічно провести вимірювання для положення всіх чотирьох вантажів на віддалі  від осі стержня і знайти середнє значення періоду .

3. Виміряти довжину стержня 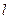 і, за допомогою мікрометра, діаметр стержня. Вимірювання цих розмірів провести декілька разів і визначити середнє значення  і 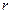. Зважуванням знайти масу вантажу .

4. Підставивши у формулу (9) середнє значення виміряних величин, вирахувати модуль зсуву. Оцінити похибки визначення модуля зсуву.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться: