Лабораторна робота № 2.02. Визначення середньої довжини вільного пробігу і ефективного діаметра молекул газу

в ступ

Середня довжина вільного пробігу молекул дорівнює віддалі, яку проходить в середньому молекула між двома послідовними співударами і характеризує всю сукупність молекул газу при даних значеннях його температури й тиску. В даній роботі для визначення середньої довжини вільного пробігу молекул використовується вираз для динамічної в’язкості газу, виведений на основі молекулярно-кінетичної теорії з урахуванням розподілу молекул за швидкостями і сил взаємодії між молекулами реального газу

, (1)

де – динамічна в’язкість, – середня швидкість хаотичного руху молекул газу, – густина газу. Відповідний вираз для ідеального газу, одержаний без врахування розподілу молекул по швидкостях, відрізняється від формули (1) тільки числовим коефіцієнтом, рівним 1/3. З формули (1) слідує

(2)

Вимірюючи на досліді динамічну в’язкість , можна за формулою (2) знайти середню довжину вільного пробігу молекул, якщо відомі середня арифметична швидкість газових молекул і густина газу . Згідно з кінетичною теорією газів

, (3)

де – молярна газова стала, – термодинамічна температура, – молярна маса газу. Густину газу можна знайти з рівнянням Менделєєва-Клапейрона

, (4)

де – тиск газу.

Середня довжина вільного пробігу залежить від ефективного діаметра молекул і числа молекул в одиниці об’єму :

(5)

Ефективний діаметр молекули – це та найменша віддаль, на яку наближаються при співударі центри двох молекул, і її можна визначити, використовуючи формулу (5), враховуючи при цьому, що число молекул в одиниці об’єму газу дорівнює

, (6)

де – постійна Больцмана, – температура, – тиск газу.

Метод визначення динамічної в’язкості повітря

В цій роботі досліджуваним газом є сухе повітря, динамічна в’язкість якого визначається на основі формули Пуазейля: (див. лаб. робота № 2.01, формула 8)

(7)

Рис. 2.4

Установка (рис. 2.4) складається з наповненого водою аспіратора 1, капіляра 2 і манометра 3. При витіканні води через кран 4 тиск в аспіраторі знижується і через капіляр в аспіратор всмоктується сухе повітря, яке попередньо проходить через осушувач 5. Різницю тисків , що виникає на кінцях капілярної трубки, вимірюється за допомогою манометра

, (8)

де – густина рідини в манометрі, різниця висот рівнів в манометрі, 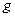– прискорення вільного падіння. Об’єм повітря, яке протікає через капіляр, визначається по об’єму води, що витікає з аспіратора.

Завдання

1. Обережно відкрити кран 4, визначити час витікання 300 мл води. Визначити за допомогою манометра різницю тисків . Дослід повторити 5-7 разів. Знайти середнє значення і .

2. Використовуючи формулу (7), визначити динамічну в’язкість . Радіус капіляра і його довжина дані як постійні приладу.

3. За формулою (3) визначити швидкість молекул газу.

4. За формулою (4) знайти густину газу. При цьому тиск повітря 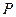, його температура визначається за показами термометра і барометра, які є в приміщенні лабораторії.

5. Використовуючи формули (5) і (6), визначити ефективний діаметр молекул повітря.

6. Знайти похибки визначення і .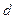

Контрольні запитання

1. В чому суть методу визначення середньої довжини вільного пробігу молекул в цій роботі?

2. Яка методика визначення динамічної в’язкості повітря в даній роботі?

3. Чому діаметр молекул називається ефективним?

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒