
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Идеализированные пассивные элементыСтр 1 из 13Следующая ⇒
Лекция 1 Курс ОТЦ является базовым для таких областей знания как электротехника и радиоэлектроника. Электромагнитные явления и устройства на их основе описываются строго методами теории электромагнитного поля. Они сложны, но описывают процессы в каждой точке электромагнитного поля. Методы теории цепей – это упрощённые методы, основанные на замене реального устройства некоторой упрощённой моделью, процессы в которой описываются токами и напряжениями. Разработка методов исследования процессов в электронных устройствах, основанных на замене этих устройств упрощенными моделями, процессы в которых описываются в терминах токов и напряжений –предмет теории цепей. 1.1. Основные определения Электрическая цепь Электрическая цепь – это совокупность устройств, образующих путь для электрического тока, электромагнитные процессы которые могут быть описаны с помощью напряжений и токов. Составные части (элементы) цепи делятся на источники электрической энергии и приёмники (нагрузки). Первичные источники электрической энергии преобразуют световую, химическую, тепловую, механическую и другие виды энергии в электрическую. Вторичные источники преобразуют вид электрических токов и напряжений за счёт преобразования постоянного тока в переменный, выпрямления переменного тока, изменения напряжения и т. п. Приемники электрической энергии преобразуют эту энергию в другие виды энергии или запасают ее. Каждый элемент цепи имеет зажимы – полюсы. Каждый элемент цепи характеризуется зависимостью между токами и напряжениями на полюсах. В теории цепей каждый элемент цепи заменяют его упрощенной моделью, построенной из идеализированных элементов. Используют пять основных типов идеализированных двухполюсных элементов: идеальный резистор, идеальный конденсатор, идеальная индуктивная катушка, идеальный источник напряжения и идеальный источник тока. Также четыре четырехполюсных идеализированных элемента: управляемые источники тока и напряжения - источник напряжения, управляемый напряжением (ИНУН), источник напряжения, управляемый током (ИНУТ), источник тока, управляемый напряжением (ИТУН), источник тока, управляемый током (ИТУТ). Электрическая цепь, составленная из идеализированных элементов, называется моделирующей идеализированной схемой замещения или эквивалентной схемой. Электрический ток
Электрический ток – это упорядоченное движение свободных носителей заряда в соединительных проводниках и внешних выводах элементов электрической цепи и внешних выводах элементов электрической цепи.За положительное направление тока принимают направление перемещения положительного заряда. Условно, положительное направление тока при расчетах электрических цепей может быть выбрано и произвольно. Если в результате расчетов, выполненных с учетом выбранного направления, ток получится со знаком плюс, то его направление, т. е. направление перемещения положительных зарядов, совпадает с направлением, условно выбранным положительным; если ток будет иметь знак минус, то его направление противоположно условно положительному. Количественно ток оценивают зарядом, проходящим через поперечное сечение проводника в единицу времени. Пусть q = q(t1) — это заряд, прошедший через произвольное поперечное сечение проводника к моменту времени t1 (рис. 1.1, а). Тогда ток в момент времени t1:
i(t)
Постоянный ток
Рис. 1.1. Зависимость заряда, протекающего через поперечное сечение проводника от времени: а — нелинейная; б — линейная
В Международной системе единиц (СИ) заряд выражают в кулонах (Кл), время — в секундах (с), ток — в амперах (А). При постоянном токе в 1 А через поперечное сечение проводника за промежуток времени, равный 1 с, переносится заряд в 1 Кл.
Напряжение На всякий заряд, помещенный в электрическое поле, действует сила, абсолютное значение и направление которой определяются напряженностью электрического поля, а также значением заряда и его знаком. Если носитель заряда является свободным,
Потенциал В Международной системе единиц напряжение измеряется в вольтах (В), а работа — в джоулях (Дж). Положительное направление напряжения выбирается от точки цепи с большим потенциалом к точке цепи с меньшим потенциалом, что соответствует перемещению положительно заряженных носителей. Внутри источников энергии носители перемещаются за счет энергии сторонних (неэлектрических) сил в направлении, противоположном направлению действия сил электрического поля. Таким образом, направление тока через источник противоположно направлению напряжения.
При расчетах электрических цепей условно положительное направление напряжения выбирается произвольно. Если в результате расчетов напряжение на рассматриваемом участке цепи получится со знаком плюс, то направление напряжения совпадает с направлением, условно принятым положительным, если напряжение получится со знаком минус, то его направление противоположно условно положительному.
u(t)
t
Электродвижущая сила
источника и противоположно внешнему напряжению. e=e(t) – функция времени e(t)=E– =const [e]=В (вольт). Мощность и энергия При перемещении элементарного электрического заряда dq между точками цепи с разностью потенциалов и совершается элементарная работа. (А=F*S; dA=FdS – работа в механике). Элементарная работа количественно равна энергии, поступившей в участок цепи за время dt. Общую энергию, поступившую в участок цепи, определяют суммированием элементарных работ: При t= Производная энергии по времени представляет собой мгновенную мощность При совпадении направлений u и i p положительна и участок цепи получает энергию. При несовпадении направлений u и i p отрицательна и участок отдает энергию.
Схемы электрической цепи Схема электрической цепи – это условное графическое изображение электрической цепи: структурные, функциональные, принципиальные и схемы замещения. Структурная схема – это отображение основных блоков устройства и связи между ними.
Функциональная схема – функциональные части с указанием их параметров и связи между ними.
Схема замещения или эквивалентная схема цепи состоит только из идеализированных элементов. Каждому реальному элементу соответствует схема замещения:
Рис. 1.2. Схема электрической цепи
Схема замещения элемента также состоит из идеализированных элементов. Разные схемы: замещения по постоянному току, по переменному току, по НЧ, по ВЧ.
Резистивный элемент Резистивным элементом или идеальным резистором называется идеализированный пассивный элемент, в котором электрическая энергия необратимо преобразуется в другие виды энергии: тепловую, световую, механическую и др. Резистивный элемент количественно характеризуется сопротивлением. Рис. 1.3. Условное графическое изображение резистивного элемента Статические вольт-амперные характеристики резистивного элемента (рис. 1.4, а — в).
Рис. 1.4. Статические вольт-амперные характеристики различных резистивных элементов
По ВАХ определяется статическое сопротивление и дифференциальное сопротивление в рабочей точке
Rст1=
Rст2= Rдиф1= Rдиф2= Лекция 2 Емкостный элемент Емкостнымэлементом, идеальным конденсатором или емкостью называется идеализированный элемент электрической цепи, запасающий энергию электрического поля. Емкость С – это количественная характеристика емкостного элемента, описывающая способность запасать энергию электрического поля.
Зависимость заряда q, накопленного в емкостном элементе от напряжения uc называется кулон – вольтной характеристикой:
Рис. 1.7. Кулон-вольтные характеристики емкостного элемента
Ccт = q/u Cдиф = dq/du. Для линейного емкостного элемента: Ccт = Cдиф= q/u; [C]=Ф (фарад). Закон Ома: Ток емкости пропорционален скорости изменения приложенного к ней напряжения: Мгновенная мощность емкости: Если
t Если
Энергия электрического поля, запасенная в емкости: Эта энергия определяется только мгновенным значением напряжения на емкости. Емкость может только запасать или отдавать электрическую энергию, но не преобразовывать. Индуктивный элемент Индуктивный элемент, идеальная индуктивная катушка или индуктивность – это идеализированный элемент цепи, в котором происходит запасание энергии магнитного поля. iL
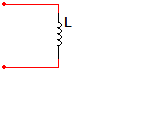 Количественно способность идеализированного элемента запасать энергию магнитного поля называют индуктивностью L. Количественно способность идеализированного элемента запасать энергию магнитного поля называют индуктивностью L.
Закон электромагнитной индукции: при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится ЭДС е, равная скорости изменения потокосцепления катушки Ψ и направленная таким образом, чтобы вызванный ею ток стремился воспрепятствовать изменению магнитного потока: Потокосцепление катушки где N — число витков катушки. [
В общем случае:
Потокосцепление самоиндукции
Закон Ома:
Напряжение Мгновенная мощность: Энергия, запасенная в индуктивности: определяется только мгновенным значением тока. C и L называются энергоемкими или реактивными. Дуальные элементы цепи Таблица: ток, напряжение, мощность и энергия идеализированных пассивных элементов
Выражения для пары R и G, а также пары L и С могут быть получены одни из других путем замены Такие пары элементов называются дуальными. Дуальными могут быть также активные элементы и электрические цепи, обладающие такими же свойствами: одинаковые соотношения, которые могу быть получены друг из друга заменой Схемы замещения реальных элементов электрических цепей. Схема замещения резистора:
Упрощенная схема замещения резистора:
Схема замещения конденсатора:
Схема замещения индуктивной катушки:
Схема замещения конденсатора на разных частотах:
а) для низких частот; б) для средних частот; в) для высоких частот; г) при постоянном токе. Идеальный источник тока Идеальный источник тока (источник тока) — это идеализированный активный элемент, ток которого не зависит от напряжения на его зажимах.

Внешняя характеристика источника тока: При При подключенной нагрузке:
При Лекция 3 «Топология цепей» Законы Кирхгофа Электрические процессы в цепях описываются компонентными и топологическими уравнениями. Компонентные уравнения или уравнения ветвей – это математические модели ветвей, которые связывают ток и напряжение ветви через параметры элементов этой ветви по закону Ома: Ветви электрической цепи делятся на вырожденные и невырожденные. Невырожденные ветви устанавливают связь между током и напряжением и имеют две формы: 1. 2. Для вырожденной ветви ток и напряжение не зависят друг от друга: 1. В ветви только источники напряжения:

2.
Топологические уравнения устанавливают связь между токами или напряжениями различных ветвей. Первый закон Кирхгофа: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов цепи, в любой момент времени равна нулю. Для каждого из узлов цепи может быть составлено уравнение баланса токов: Коэффициент аlk = 1, если k-я ветвь подключена к l-му узлу и ток ветви направлен от узла; аlk = −1, если k-я ветвь подключена к l-му узлу и ток ветви направлен к узлу; аlk = 0, если k -я ветвь не подключена к l-му узлу. (1): (0) i1 + i2 ― i6 = 0. Если записать сумма мгновенных значений токов, направленных к любому узлу цепи, в любой момент времени равна сумме токов, направленных от этого узла. Второй закон Кирхгофа: алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур цепи, в каждый момент времени равна нулю. Для каждого контура можно составить уравнение баланса напряжений ветвей: k — номера ветвей; р — число ветвей; n — номера контуров; N — число контуров. blk = 1, если k-я ветвь входит в l-й контур и направление напряжения ветви совпадает с направлением обхода контура; blk = −1, если k-я ветвь входит в l-й контур и направление ее напряжения противоположно направлению обхода контура; blk = 0, если k-я ветвь не входит в l-й контур. 1. – u1 + u2 = 0; 2. – u2 + u3 = 0; Уравнения по второму закону Кирхгофа можно составить и для напряжений всех элементов, входящих в контур: или В общем виде: Из этого может быть следующая формулировка второго закона Кирхгофа: алгебраическая сумма мгновенных значений напряжения всех элементов любого контура моделирующей цепи, за исключением источников напряжения, в каждый момент времени равна алгебраической сумме мгновенных значений ЭДС источников напряжения, действующих в этом контуре. Общее число уравнений баланса токов и напряжений равно сумме числа узлов и числа контуров исследуемой цепи. Однако, часть этих уравнений линейно зависима, т.е. могут быть получены одни из других. Определение числа линейно независимых уравнений осуществляется с помощью теории графов. Лекция 4 Метод комплексных амплитуд В установившемся режиме токи и напряжения всех ветвей линейной цепи, находящейся под гармоническим воздействием, являются гармоническими функциями времени той же частоты, и, следовательно, задача анализа цепи состоит в нахождении начальных фаз и амплитуд необходимых токов и напряжений. Метод комплексных амплитуд относится к символическим методам, основанным на преобразовании исходных функций, называемых оригиналами, в другие функции, называемых изображениями или символами. При этом операции над исходными функциями заменяются более простыми операциями над изображениями. Таким образом, символические методы содержат три этапа: 1. прямое преобразование от оригиналов к изображениям; 2. определение изображений искомых величин; 3. обратное преобразование от изображений к оригиналам. Метод комплексных амплитуд основан на представлении гармонических функций времени с помощью комплексных чисел. Комплексным числом А называется выражение вида где А', А" — действительные числа, называемые, соответственно, вещественной и мнимой составляющими комплексного числа; Изображение вещественного числа на числовой оси:
Комплексно – сопряженные числа: A = A' + jA''= Операции сложения и вычитания лучше делать в алгебраической форме:
Сумма двух сопряженных чисел:

Умножение и деление комплексных чисел можно производить также и в показательной форме:
Деление:

Возведение в степень: Умножение на число:
При умножении на
 
Умножение вектора А = а умножение вектора А на вектор Лекция 5 Комплексные сопротивление и проводимость пассивного участка цепи. Выделим двухполюсный участок цепи без источников энергии:
Комплексным входным сопротивлением (комплексным сопротивлением) Z пассивного участка цепи называется отношение комплексной амплитуды напряжения на зажимах участка цепи к комплексной амплитуде тока: Комплексное сопротивление – это комплексное число: z = |Z| - модуль комплексного сопротивления или полное входное сопротивление; φ – аргумент комплексного сопротивления; r – вещественная (резистивная) составляющая;
Величина, обратная комплексному входному сопротивлению, называется комплексной входной проводимостью участка цепи:
g = y cos Связь между мнимыми и вещественными составляющими комплексного сопротивления и комплексной проводимости: Резистивный элемент
найти: iR , ZR
Энергия, поступившая в резистивный элемент:
Комплексные ток и напряжение резистивного элемента:
Комплексное сопротивление:
Схема замещения
Комплексная проводимость резистивного элемента: YR = 1/ZR = 1/R = G.
Емкостный элемент
ψi = ψu + π/2, - ток емкости опережает по фазе напряжение на 90°
IC = ωCUC
Энергия:
Комплексные ток и напряжение емкости:
Комплексное сопротивление емкости:
Комплексная схема замещения
rC = 0; хC = −1/(ωС); zC = 1/(ωC); φC = −π/2
Комплексная проводимость емкости:
Индуктивный элемент UL = ωLiL
Комплексные ток İL и напряжение ŮL:
Комплексная проводимость:
Лекция 6 Последовательная RL -цепь
Найдем Искомые Перейдем к комплексным схемам замещения элементов: Перейдем к комплексным изображениям переменных:
Получим комплексную схему замещения цепи:
Через законы Ома и Кирхгофа составляем систему уравнений электрического равновесия цепи:
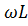 ; ;  ; ;  ; ; 
Положение вектора комплексного сопротивления определяет характер цепи. В общем случае, если: |φ| = π/2 – входное сопротивление имеет чисто реактивный (мнимый) характер: Находим комплексное действующее значение тока:
Треугольник напряжений подобен треугольнику сопротивлений. При гармоническом воздействии задача анализа цепи считается решенной, если получены комплексные значения искомых функций.
Оригинал: Последовательная RC – цепь Задано: найдем комплексный ток и комплексное входное сопротивление цепи.
Система уравнений электрического равновесия: ZR = R; ZC=1/(jωC);
Векторная диаграмма входного сопротивления цепи:
−π/2 < φ < 0 – резистивно – емкостной характер; Векторные диаграммы тока и напряжений:
Последовательная RLC – цепь
Комплексная схема замещения
Законы Ома и Кирхгофа: Характер цепи определяется соотношением между сопротивлением индуктивности xL = ωL и сопротивлением емкости хC = −1/(ωC).
Векторные диаграммы входного сопротивления цепи:
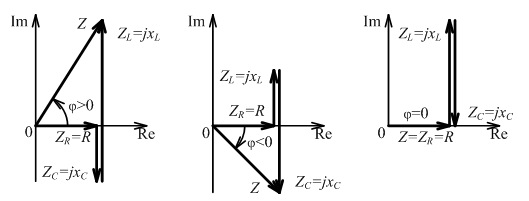
Векторные диаграммы тока и напряжений:

Параллельная RLC – цепь
где YR=1/R; YС = jωС; YL=1/(jωL)
Y = YR + YC + YL=1/R+ jωС+1/(jωL)=
Векторные диаграммы входной проводимости цепи:
Векторные диаграммы токов и напряжений:
Делители напряжения и тока Делитель напряжения
она же:
Z1 и Z2 могут состоять из нескольких идеализированных элементов:

Цепи такого типа называют делителями напряжения, а элементы Z1 и Z2 – плечами делителями.
Комплексные коэффициенты передачи делителя напряжения или коэффициент деления: при Делитель тока дуален по отношению к делителю напряжения.
Комплексные коэффициенты передачи делителя тока или коэффициенты деления.
Лекция 7 Баланс мощностей Пусть цепь содержит N идеальных источников напряжений, M идеальных источников тока и H идеальных пассивных элементов, ik , uk — ток и напряжение k-то элемента цепи. Из закона сохранения энергии следует, что сумма мгновенных мощностей всех элементов цепи в каждый момент времени равна нулю: сумма мгновенных мощностей, отдаваемых всеми источниками, равна сумме мгновенных мощностей, потребляемых всеми приемниками энергии. Для комплексных мощностей: Для практических расчетов используют уравнение:
 положительные направления токов и напряжений источников (ток и напряжение направлены в разные стороны). положительные направления токов и напряжений источников (ток и напряжение направлены в разные стороны).
Из условия баланса комплексных мощностей следует условие баланса активных мощностей: и условие баланса реактивных мощностей: Коэффициент мощности определяется входным сопротивлением цепи. Величина cos φ = PA/PS , характеризующая степень приближения активной мощности цепи к максимальному значению мощности, называется коэффициентом мощности. Наивысшее значение коэффициент мощности (cos φ = 1) имеет при чисто резистивном характере нагрузки φ=0. Если реальная нагрузка имеет резистивно-емкостный или резистивно-индуктивный характер ZH = rн + jxн, YH = gн + jbн, то параллельно или последовательно ей можно подключить компенсирующий элемент с чисто реактивным сопротивлением или проводимостью, равной по абсолютному значению, но противоположной по знаку мнимой составляющей нагрузки. Тогда сопротивление участка цепи, представляющего собой последовательное или параллельное соединение нагрузки и компенсирующего элемента, будет иметь чисто реактивный характер.
Лекция 8 Преобразования электрических цепей Преобразование электрических цепей осуществляется с целью упрощения последующего анализа. Преобразование состоит в замене участков цепи на более простые. Два участка цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не изменяются. Эквивалентные участки цепи обладают следующими свойствами: 1. симметричности: цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А; А Б 2. транзитивности: если цепь А эквивалентна цепи Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными; А Б В, то А В. Два участка цепи полностью эквивалентны, если они эквивалентны для любых внешних воздействий и частично эквивалентны, если они эквивалентны для определенных внешних воздействий. Эквивалентные преобразования цепей основаны на эквивалентных преобразованиях соответствующих систем уравнений электрического равновесия. Перенос источников Схема с вырожденным источником Схема с перенесенным источником:
Вырожденный источник напряжения переносится последовательно в ветви, подключенной к этому источнику с сохранением величины и направления. Узлы, между которыми был подключен источник, объединяются в один. Схема с вырожденным Схема с перенесенным источником тока
(1) (2) (3) 1. 2. Вырожденный источник тока переносится параллельно ветви, подключенной параллельно с сохранением величины и направления. Ветвь с источником исчезает.
Лекция 9
Лекция 10 ФНЧ Для CR – цепи: ФВЧ Логарифмические АЧХ и ФЧХ При изменении частоты в широких пределах удобно использовать логарифмические масштабы по осям
АЧХ, построенная в логарифмическом масштабе, называется логарифмической АЧХ (ЛАЧХ). ФЧХ, построенная в логарифмическом масштабе по оси, ЛФЧХ.
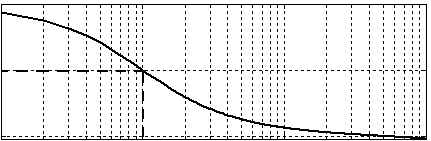
ЛАЧХ ФНЧ:
ЛФЧХ ФНЧ:
ЛАЧХ ФВЧ:
ЛФЧХ ФВЧ:
Лекция 11 Лекция 12 Лекция 13 Метод контурных токов (КТ) Можно показать, что из p – токов ветвей только токи главных ветвей числом p – q + 1 являются независимыми, обычно q – 1<p. Будем называть их контурными токами. Остальные токи, т.е. ветвей дерева, могут быть найдены из контурных, применяя УБТ. Для примера №1 УБТ: Токи главных ветвей: Тогда токи ветвей дерева: Подставим в УБН, получим систему контурных уравнений цепи: Введем новые понятия: Собственным сопротивлением Контурный ток i-гo контура обозначим Общим или взаимным сопротивлением i-гo и j-гo контуров назовем сопротивление Общее сопротивление Если контуры не имеют общих ветвей, то общее сопротивление равно нулю. Контурная ЭДС Если направление ЭДС совпадает с направлением контурного тока, плюс. Контурные уравнения в канонической (стандартной) форме: Такая же система уравнений будет для цепи, содержащей произвольное n число главных контуров. В матричной форме система контурных уравнений: i=1,…,n; j=1,…,n; — квадратная симметричная
При наличии ветвей с источниками тока их либо преобразуют в ветви с источниками напряжения, либо при выборе дерева графа все источники тока заданы и не требуют определения. Для неизвестных контурных токов составляется система из р − q + 1 –рит уравнений. Таким образом, порядок составления контурных уравнений следующий: 1) построение графа цепи, выбор дерева графа, выделение главных контуров; 2) определение числа уравнений n и запись системы в канонической; 3) нахождение элементов матриц контурных сопротивлений Метод узловых напряжений Узловое напряжение – это напряжение i– го узла цепи относительно базового Напряжения всех ветвей цепи могут быть выражены через узловые:
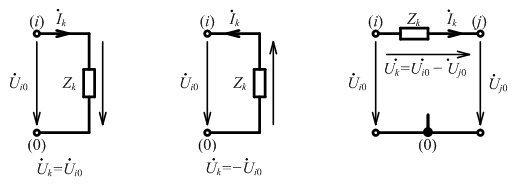
Если цепь не содержит вырожденных ветвей рин, то все q – 1 неизвестные узловые напряжения независимы. ССУ относительно узловых напряжений называется системой узловых уравнений цепи. Метод формирования такой системы называется методом узловых напряжений.
УБТ: Выразим токи ветвей через напряжение ветвей, а напряжение ветвей через узловые напряжения: Представим в УБТ: Введем понятия: Собственная проводимость Общая (взаимная) проводимость i-гo и j-гo узлов Если в цепи нет ветви между i-м и j-м узлами, то Узловым током Если источник тока направлен к узлу, то плюс. Таким образом, узловые уравнения в канонической форме: Для цепи с m=q – 1 независимыми узлами в матричной форме:
При При наличии источников напряжения в цепи они либо с помощью эквивалентных преобразований преобразуются в источники тока, либо включаются в дерево графа, затем определяется Лекция 14 Теорема компенсации Токи и напряжения ветвей произвольной цепи не изменятся, если любую ветвь этой цепи заменить идеальным источником ЭДС, напряжение и направление которого равны напряжению данной ветви, либо идеальным источником тока, ток и направление которого совпадают с током данной ветви.
При составлении УБТ вместо цепи эквивалентны. Используемые источники являются управляемыми: Из условий эквивалентности следует, что управляемые источники вида могут быть заменены на комплексное сопротивление Zk.
Лекция 15 Лекция 16 Лекция 1 Курс ОТЦ является базовым для таких областей знания как электротехника и радиоэлектроника. Электромагнитные явления и устройства на их основе описываются строго методами теории электромагнитного поля. Они сложны, но описывают процессы в каждой точке электромагнитного поля. Методы теории цепей – это упрощённые методы, основанные на замене реального устройства некоторой упрощённой моделью, процессы в которой описываются токами и напряжениями. Разработка методов исследования процессов в электронных устройствах, основанных на замене этих устройств упрощенными моделями, процессы в которых описываются в терминах токов и напряжений –предмет теории цепей. 1.1. Основные определения Электрическая цепь Электрическая цепь – это совокупность устройств, образующих путь для электрического тока, электромагнитные процессы которые могут быть описаны с помощью напряжений и токов. Составные части (элементы) цепи делятся на источники электрической энергии и приёмники (нагрузки). Первичные источники электрической энергии преобразуют световую, химическую, тепловую, механическую и другие виды энергии в электрическую. Вторичные источники преобразуют вид электрических токов и напряжений за счёт преобразования постоянного тока в переменный, выпрямления переменного тока, изменения напряжения и т. п. Приемники электрической энергии преобразуют эту энергию в другие виды энергии или запасают ее. Каждый элемент цепи имеет зажимы – полюсы. Каждый элемент цепи характеризуется зависимостью между токами и напряжениями на полюсах. В теории цепей каждый элемент цепи заменяют его упрощенной моделью, построенной из идеализированных элементов. Используют пять основных типов идеализированных двухполюсных элементов: идеальный резистор, идеальный конденсатор, идеальная индуктивная катушка, идеальный источник напряжения и идеальный источник тока. Также четыре четырехполюсных идеализированных элемента: управляемые источники тока и напряжения - источник напряжения, управляемый напряжением (ИНУН), источник напряжения, управляемый током (ИНУТ), источник тока, управляемый напряжением (ИТУН), источник тока, управляемый током (ИТУТ). Электрическая цепь, составленная из идеализированных элементов, называется моделирующей идеализированной схемой замещения или эквивалентной схемой. Электрический ток
Электрический ток – это упорядоченное движение свободных носителей заряда в соединительных проводниках и внешних выводах элементов электрической цепи и внешних выводах элементов электрической цепи.За положительное направление тока принимают направление перемещения положительного заряда. Условно, положительное направление тока при расчетах электрических цепей может быть выбрано и произвольно. Если в результате расчетов, выполненных с учетом выбранного направления, ток получится со знаком плюс, то его направление, т. е. направление перемещения положительных зарядов, совпадает с направлением, условно выбранным положительным; если ток будет иметь знак минус, то его направление противоположно условно положительному. Количественно ток оценивают зарядом, проходящим через поперечное сечение проводника в единицу времени. Пусть q = q(t1) — это заряд, прошедший через произвольное поперечное сечение проводника к моменту времени t1 (рис. 1.1, а). Тогда ток в момент времени t1:
i(t)
Постоянный ток
Рис. 1.1. Зависимость заряда, протекающего через поперечное сечение проводника от времени: а — нелинейная; б — линейная
В Международной системе единиц (СИ) заряд выражают в кулонах (Кл), время — в секундах (с), ток — в амперах (А). При постоянном токе в 1 А через поперечное сечение проводника за промежуток времени, равный 1 с, переносится заряд в 1 Кл.
Напряжение На всякий заряд, помещенный в электрическое поле, действует сила, абсолютное значение и направление которой определяются напряженностью электрического поля, а также значением заряда и его знаком. Если носитель заряда является свободным,
Потенциал В Международной системе единиц напряжение измеряется в вольтах (В), а работа — в джоулях (Дж). Положительное направление напряжения выбирается от точки цепи с большим потенциалом к точке цепи с меньшим потенциалом, что соответствует перемещению положительно заряженных носителей. Внутри источников энергии носители перемещаются за счет энергии сторонних (неэлектрических) сил в направлении, противоположном направлению действия сил электрического поля. Таким образом, направление тока через источник противоположно направлению напряжения.
При расчетах электрических цепей условно положительное направление напряжения выбирается произвольно. Если в результате расчетов напряжение на рассматриваемом участке цепи получится со знаком плюс, то направление напряжения совпадает с направлением, условно принятым положительным, если напряжение получится со знаком минус, то его направление противоположно условно положительному.
u(t)
t
Электродвижущая сила
источника и противоположно внешнему напряжению. e=e(t) – функция времени e(t)=E– =const [e]=В (вольт). Мощность и энергия При перемещении элементарного электрического заряда dq между точками цепи с разностью потенциалов и совершается элементарная работа. (А=F*S; dA=FdS – работа в механике). Элементарная работа количественно равна энергии, поступившей в участок цепи за время dt. Общую энергию, поступившую в участок цепи, определяют суммированием элементарных работ: При t= Производная энергии по времени представляет собой мгновенную мощность При совпадении направлений u и i p положительна и участок цепи получает энергию. При несовпадении направлений u и i p отрицательна и участок отдает энергию.
Схемы электрической цепи Схема электрической цепи – это условное графическое изображение электрической цепи: структурные, функциональные, принципиальные и схемы замещения. Структурная схема – это отображение основных блоков устройства и связи между ними.
Функциональная схема – функциональные части с указанием их параметров и связи между ними.
Схема замещения или эквивалентная схема цепи состоит только из идеализированных элементов. Каждому реальному элементу соответствует схема замещения:
Рис. 1.2. Схема электрической цепи
Схема замещения элемента также состоит из идеализированных элементов. Разные схемы: замещения по постоянному току, по переменному току, по НЧ, по ВЧ.
Идеализированные пассивные элементы Резистивный элемент Резистивным элементом или идеальным резистором называется идеализированный пассивный элемент, в котором электрическая энергия необратимо преобразуется в другие виды энергии: тепловую, световую, механическую и др. Резистивный элемент количественно характеризуется сопротивлением. Рис. 1.3. Условное графическое изображение резистивного элемента Статические вольт-амперные характеристики резистивного элемента (рис. 1.4, а — в).
Рис. 1.4. Статические вольт-амперные характеристики различных резистивных элементов
По ВАХ определяется статическое сопротивление и дифференциальное сопротивление в рабочей точке
Rст1=
Rст2= Rдиф1= Rдиф2= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2019-04-19; Просмотров: 1192; Нарушение авторского права страницы