Анализ простейших линейных цепей при гармоническом воздействии

Последовательная RL -цепь

Задано:

;

Найдем  методом комплексных амплитуд.

Искомые .

Перейдем к комплексным схемам замещения элементов:

Перейдем к комплексным изображениям переменных:

 

Получим комплексную схему замещения цепи:

                                  

 

 

Через законы Ома и Кирхгофа составляем систему уравнений электрического равновесия цепи:

; Z = Z_R + Z_L= R + jωL ― комплексное входное coпротивление цепи.

 

Векторная диаграмма входного сопротивления цепи:

Z

r=R; x= ; ; ;

 

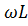Положение вектора комплексного сопротивления определяет характер цепи. В общем случае, если:

|φ| = π/2 – входное сопротивление имеет чисто реактивный (мнимый) характер:

 

Находим комплексное действующее значение тока:

;

Векторная диаграмма тока и напряжений:

.

Треугольник напряжений подобен треугольнику сопротивлений.

 При гармоническом воздействии задача анализа цепи считается решенной, если получены комплексные значения искомых функций.

 

 

Оригинал:

Последовательная RC – цепь

Задано: ;

найдем комплексный ток и комплексное входное сопротивление цепи.

Перейдем к схеме замещения :

 

 

Система уравнений электрического равновесия:

;

Z_R = R; Z_C=1/(jωC); ;

 

 

 

Векторная диаграмма входного сопротивления цепи:

;

−π/2 < φ < 0 – резистивно – емкостной характер;

;

Векторные диаграммы тока и напряжений:

 

Последовательная RLC – цепь

 

Комплексная схема замещения

 

 

Законы Ома и Кирхгофа:

 где Z_R = R; Z_L = jωL; Z_C = 1/(jωC);

;

Характер цепи определяется соотношением между сопротивлением индуктивности x_L = ωL и сопротивлением емкости х_C = −1/(ωC).

 

 Векторные диаграммы входного сопротивления цепи:

xL = |xC|; φ =0: резистивный характер

xL > |xC|; 0 < φ < π/2: резистивно – индуктивный характер

xL < |xC|; -π/2 < φ <0 : резистивно – емкостной характер

 

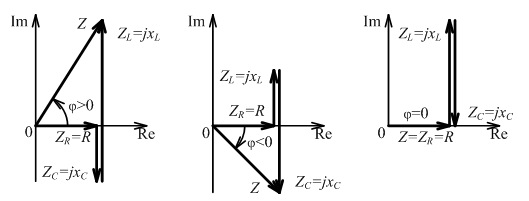
Векторные диаграммы тока и напряжений:

,+90о

,-90о

,0о

 

Параллельная RLC – цепь

В комплексной схеме замещения будем использовать комплексные проводимости:

 

где Y_R=1/R; Y_С = jωС; Y_L=1/(jωL)

Y = Y_R + Y_C + Y_L=1/R+ jωС+1/(jωL)= ;

 

Векторные диаграммы входной проводимости цепи:

bC > |bL| 0 <  < π/2 резистивно – емкостной характер

bC =|bL|  =0 резистивный характер

|bL| > bC -π/2 <  <0 резистивно – индуктивный характер

 

 

 

Векторные диаграммы токов и напряжений:

 

 

Последовательная и параллельная RLC- цепи дуальны, так как выражения одинаковы при замене u на i, R на Y, С на L.

Делители напряжения и тока

Делитель напряжения

Рассмотрим цепь:

она же:  

 

 

Z₁ и Z₂ могут состоять из нескольких идеализированных элементов:

Z1

Z2

 

Цепи такого типа называют делителями напряжения, а элементы Z₁ и Z₂ – плечами делителями.

;

;

 

Комплексные коэффициенты передачи делителя напряжения или коэффициент деления:

при

Делитель тока дуален по отношению к делителю напряжения.

 

Комплексные коэффициенты передачи делителя тока или коэффициенты деления.

 

Лекция 7

⇐ Предыдущая234567891011Следующая ⇒

Поделиться: