Еквівалентність обох означень.

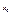Озн. Нех. деяка мн.R чисел. Тоді т.  наз. граничною т. мн.E, якщо в околі цієї т. є безліч ел-тів мн.E. Якщо E скла-дається із скінченої к-сті точок, то граничної точки вона не має.

П-д. Мн. . Тут кожна точка цього відрізка є його граничною точкою (і всі граничні точки цієї мн. їй належать).

Т. (Властивість граничної точки множини):

Якщо 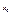 гранична т. мн.Е, то $ :

Дов. Візьм. т.я. в ньому безліч ел-тів, то візьм. з них і познач. .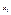

Візьм.  в ньому теж безліч ел-тів, тому $ :

……………….

В знайдемо :

В результаті ми одерж. всі члени якої відрізняються між собою, всі  і як Þ з ост. нерівності (за т. про 2 міліціонери).

Озн. (гр. ф-ції за Гейне). Число А наз. границею ф-ції в т. 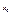 ( ) і записується , якщо

 

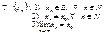
матимемо, що А. Якщо співставити тільки що проведене озн. із озн. границі посл., одержимо:

Озн. (гр. ф-ції за Коші). Число А наз. границею ф-ції в т. 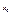 ( ) записується , якщо .

Т. (Еквівалентність)

Озн. Гейне і Коші границі ф-ції в т. 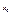– еквівалентні.

Дов. Нех. в розумінні озн. Коші. Доведемо, що в розумінні озн. Гейне. З умови маємо:  (1).

Візьмемо з такими властивостями:

 (*)

З останньої рівності за озн. границі посл. будемо мати, що для вказаного в (1) 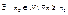, . Враховуючи дві інші власт. будемо мати, що . Звідси за (1) Þ . А це озн., що . А це озн. (Див.*), що число А– є границею ф-ції 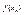 за Гейне.

Нех. число А є границею ф-ції 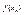за Гейне. Доведемо, що A– є границею за Коші. З умови Þ

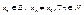
Треба довести (1). МВС: Нех. (1) – не вірне

 (2)

Поск. (2) справедливе , то воно буде справедливе і для . Покладемо в (2), що :

:

:

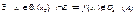
В результаті цього одержали та . :

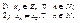
Þ за т. про два міліціонери .

Отже,  задовольняє всім вимогам із озн. Гейне. Розгл.  З її побудови Þ ні один її член 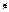Þ А – не є границею  Отже, озн. Гейне на нашій  не спрацьовує, але за умовою А – є границею ф-ції за Гейне, значить це озн. вірне з відповідними властивостями. Одержана суперечність і доводить всю нашу теорему.

Озн. Коші можна написати по-іншому, замінивши при-належність до околу відповідною нерівністю.

Озн: (Коші). , якщо .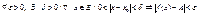

 

***29. Застосування інтеграла Рімана для обчислення площ плоских фігур в прямокутній та полярній системі координат.

 Нехай маємо фігуру яка обмежена знизу прямою y=0. З боків прямими x=a , x=b, a<b, і зверху графіком ф-ції y=f(x) про яку відомо, що f(x)  і 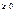на ньому. З’ясуємо, що таке площа такої трапеції і як її шукати.

Візьмемо   і знайдемо  і замінимо цю трапецію прямокутником. Площу цього прямокутника приймемо за площу трапеції S. Точність буде низькою, бо значення ф-ції в інших точках буде серйозно відрізнятися від значення в т. . Щоб уникнути цього треба розбити [a,b] на маленькі []. Візьмемо  точку і обчислимо значення ф-ції в ній, замінимо маленьку трапецію прямокутником з цією основою і висотою f(x), то 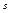 прямокутника мало відрізняється від S – трапеції, бо ф-ція f(x)  а отже значення її в всіх інших точках малого відрізка мало відрізнятиметься від вибраного нами значення.

Одержимо алгоритм вирішення вище поставленої проблеми.

Візьмемо  через одержані точки до осі OX проводимо прямі. Вони розбивають нашу трапецію на n маленьких трапецій. Беремо трапецію з основою [ ] . Візьмемо т.  замінимо цю трапецію прямокутником з цією основою і висотою f(  ) Площа цієї к+1 трапеції площі цього прямокутника  f(  )*  тоді площа всієї трапеції S

При подрібненні цього розбиття точність формули буде підвищуватися і вона перетвориться в точну при переході до границі правої частини при .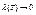

Озн. Під площею криволінійної трапеції будемо розуміти якщо вона $.

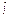Під знаком остатньої границі строїть інтегральна сума ф-ції f(x) на [a,b] , оск. , то . Згідно 2-го озн.  розглянена границя $ і  S=

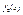Обчислимо площі більш загальної криволінійної трапеції обмеженою прямими x=a , x=b, a<b, y=  , y= . , , нех. . Коли ≥0 то площа S= . Якщо <0 позначимо m=min , m<0.Розгл. далі дві ф-ції y= і y= 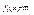. Розгл. фігуру обмежену цими ф-ціями і прямими x=a , x=b це буде нова криволінійна трапеція, яка одержується з попередньої паралельним перенесенням на вектор (0,-m). При чому графік 2-ої ф-ції буде знаходитися не нижче OX. Для обчислення S цієї трапеції викор. одержану формулу. Оск. ця трапеція є паралельним перенесенням заданої трапеції то вона їй рівна, тому S нової і S заданої співпадають.

S= =

Площа криволінійної трапеції шукається за формулою S=

⇐ Предыдущая12345678Следующая ⇒

Поделиться: