Функция распределения ДСВ и ее свойства

Две случайные величины могут иметь одинаковые возможные значения, но принимать их с различными вероятностями (например, оценки на экзамене у сильных и слабых студентов могут иметь одинаковые возможные значения, но с разными вероятностями). То есть, для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, необходимо еще указать и вероятности, с которыми она может их принимать.

Для установления связи между значениями случайной величины и их вероятностями вводят понятие закона распределения.

Законом распределения дискретной случайной величины называют правило, по которому каждому возможному значению x_i ставится в соответствие вероятность p_i , с которой случайная величина Х может принять это значение.

Закон распределения дискретной случайной величины может быть задан графически, аналитически и таблично. В последнем случае задается таблица, где в одной строке записаны все возможные значения x_i, а в другой - соответствующие им вероятности p_i:     X  x₁  x₂  .   .   .   x_n

                                     P  p ₁ p ₂ .   .   .   p_n

Поскольку в результате опыта случайная величина может принять одно и только одно из возможных значений, то события, заключающиеся в том, что Х примет значение х₁, х₂, …, х _n попарно несовместны и в сумме образуют достоверное событие, то есть                              (2.1)

 

Задача 2.1. Абитуриент сдает два вступительных экзамена: по математике и физике. Составить закон распределения случайной величины Х - числа полученных пятерок, если вероятность получения пятерки по математике равна 0,8, по физике – 0,6.

Решение. Пусть А₁ и А₂ - события, заключающиеся в том, что и математика, и физика, соответственно, сданы на «5». Очевидно, возможные значения ξ – количества «пятерок» есть 0, 1, 2, причем

При вычислении вероятностей использовались несовместность слагаемых и независимость (рис. 2.1) сомножителей. Сведем полученные данные в таблицу

Х	0	1	2
Р	0,08	0,44	0,48

 

Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (х _i , р _i ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Для рассматриваемого примера

многоугольник распределения имеет вид:

 

1

0

xi

2

                                              

Рис. 2.1.

Задача 2.2. Вероятность появления события А при одном испытании равна р. Испытания повторяются до появления события А. Составить закон распределения случайной величины ξ – числа испытаний, проведенных до первого появления А.

Решение. Возможные значения Х–целые числа от 1 до ∞. Предположим, что Х = n и найдем вероятность такого события. Очевидно, оно произойдет, если в первых n-1 испытаниях произойдут события , а в (n+1)-ом испытании произойдет событие А. Отсюда, искомая вероятность равна           

Здесь q =1- p и мы воспользовались независимостью сомножителей.

Задача 2.3. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X - стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение. Напишем возможные значения X: х₁ = 50, х₂= 1, х₃ = 0. Вероятности этих возможных значений таковы: р₁ = 0,01; р₂ = 0,1; p₃=l-(р₁ + р₂) = 0,89.   I

Напишем искомый закон распределения:       X      50    1          0         

р 0,01 0,1 0,89

Контроль: 0,01+0,1+0,89=1.

Задача 2.4. (Письм., с.63). В урне 8 шаров, из которых 5 белых, остальные – черные. Из нее вынимают наугад 3 шара. Найти закон распределения числа белых шаров в выборке.

Решение. Возможные значения С.В. Х – числа белых шаров в выборке есть х₁=0, х₂=1, х₃=2, х₃=3. Вероятности их, соответственно, будут

Закон распределения СВ имеет вид

                

Х	0	1	2	3
Р	1/56	15/56	30/56	10/56

 

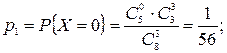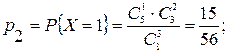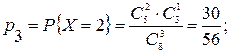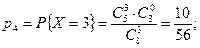
(Контроль:

Для задания любой случайной величины можно ввести понятие функции распределения.

Функцией распределения случайной величины Х называется функция F ( x ), которая для любого числа х равна вероятности того, что случайная величина Х примет значение, меньшее х:     F ( x ) = p (Х < x ).        ….     .(2.2)

При известном законе распределения функция распределения дискретной случайной величины имеет вид:                   (2.3)

где (x_i < x) означает, что суммирование ведется по всем индексам i, для которых это неравенство выполняется.

Функция распределения ДСВ обладает следующими свойствами:

1. Функция распределения F(x) ограничена, т.е. 0≤ F(x) ≤ 1.

2. Функция распределения – неубывающая функция на множестве R,

т.е., если х₂ > х₁, то     F(x₂) ≥ F(x₁).

3. Функция распределения обращается в ноль на минус бесконечности и равна единице в плюс бесконечности, т.е. F(- ∞) = 0, F(+ ∞) = 1.

4. Вероятность попадания случайной величины Х в промежуток [a, b) равна приращению функции распределения на этом промежутке, т.е.

Р{a ≤ X ≤ b} = F(b) - F(a)

5. Функция распределения непрерывна слева, т.е.

Функция распределения F ( x ) дискретной случайной величины Х является ступенчатой, сохраняющей постоянное значение на каждом интервале, не содержащем точек x_i, и терпящей в этих точках скачок, равный p_i.

Для задачи 2.1 о количестве пятерок функция распределения ДСВ и ее график (рис. 2.2) представлены ниже

 

 

                                                

Рис. 2.2.

Домашнее задание: ДР-2.1

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться: