Нахождение аналитических описаний вероятности разрушения

 

Полученное из эксперимента распределение дифференциальной вероятности разрушения хрупких волокон асимметрично. Такое распределение хорошо моделируется моделью Вейбулла. Поиск аналитических выражений, описывающих графики гладкими функциями, следует начинать с описания интегральной вероятности разрушения в виде (14) или (14*):

                                    (14)

                              (14*)

где параметры β (параметр формы распределения), s₀ (параметр размера распределения) и σ _u (корректирующий параметр)– должны быть найдены по экспериментальным данным. Доказано, что

                                       (15)

Тогда для рассматриваемого ряда .

Для нахождения параметра s₀ можно использовать два приема. Рекомендуется [1] воспользоваться квантилем уровня P = 0, 632. Как это видно на рис. 31, функция G_эксп( s ) в этой точке определяется напряжением, которому соответствует 7-ой интервал, т.е. s = 3500 МПа (точка А на рис. 31). Сделав соответствующие подстановки в выражение (14), получим:

,

а искомая функция имеет вид:

                            (16)

Кроме того, по гистограмме легко определить, что при  вероятность разрушения соответственно равна (точка B на рис. 31). Тогда можно записать:

В результате получено другое аналитическое выражение для интегральной вероятности разрушения исследуемой нити, которое имеет вид:

                            (17)

Полученные выражения позволяют заменить ступенчатую функцию монотонной гладкой кривой.

Корректность любого описания определяется близостью друг к другу площадей фигур, ограниченных ступенчатой и гладкой кривой. Для оценки правильности выбора закона распределения применяют статистическую оценку гипотез. При такой оценке сопоставляются эмпирическое распределение и аналитическое описание, найденное по его параметрам. Мерами близости служат различные «критерии согласия», установленные Пирсоном, Колмогоровым и др. для различных объемов выборок.

При объеме выборки N » 100 или более применяется критерий Колмогорова-Смирнова. С целью проверки нулевой гипотезы о соответствии подсчитывается накопленная частость и значение описывающей функции. Критерий Колмогорова-Смирнова l устанавливает близость эмпирического распределения к аналитическому описанию на основе вероятности P(l), где l вычисляется по формуле:

                                      (18)

где D_max – максимальная разность между накопленными частостями эмпирического и вычисленного распределений.

Для значений P(l) составлена табл. 13. Если вероятность меньше 0, 05, то расхождение между распределениями считается существенным и гипотеза отвергается.

Таблица 13

Вероятности P(l), соответствующие различным значениям l

l	P( l)	l	P( l)	l	P( l)
0, 3 0, 35 0, 4 0, 45 0, 5 0, 55 0, 6 0, 65 0, 7 0, 75	1, 0000 0, 9997 0, 9972 0, 9874 0, 9639 0, 9228 0, 8643 0, 7920 0, 7112 0, 6272	0, 8 0, 85 0, 9 0, 95 1, 00 1, 10 1, 20 1, 30 1, 40 1, 50	0, 5441 0, 4653 0, 3927 0, 3275 0, 2700 0, 1777 0, 1112 0, 0681 0, 0397 0, 0222	1, 60 1, 70 1, 80 1, 90 2, 00 2, 10 2, 20 2, 30 2, 40 2, 50	0, 0120 0, 0062 0, 0032 0, 0015 0, 0007 0, 0003 0, 0001 0, 0001 0, 0000 0, 0000

 

Для проверки гипотез (16) и (17) вычислим накопленные частости для середины интервалов исследуемого ряда и оценим максимальные разности D_max (табл. 14).

Таблица 14

Таблица проверки гипотез

№	Границы интервала, МПа	Середина интервала, МПа	Эксперимент. накопленная частость	Аналит. опис		Разность D
				ф. 16	ф. 17	ф. 16	ф. 17
1	2200 - 2400	2300	2	1	0	1	2
2	2400 - 2600	2500	2	1	1	1	1
3	2600 - 2800	2700	4	4	3	0	1
4	2800 - 3000	2900	8	9	8	-1	0
5	3000 - 3200	3100	19	19	18	0	1
6	3200 - 3400	3300	37	37	34	0	3
7	3400 - 3600	3500	68	61	58	7	10
8	3600 - 3800	3700	90	83	81	7	9
9	3800 - 4000	3900	96	94	93	2	3

 

При использовании формулы (16) наибольшая разность между накопленными частостями D_max = 7. Следовательно . По табл. 13 P(l) ≈ 0, 68, т.е. теоретическое описание (16) очень близко к эмпирическому распределению.

При использовании формулы (17) наибольшая разность между накопленными частостями D_max = 10. Следовательно . По табл. 13 P(l) ≈ 0, 23, что достаточно велико в сравнении со значение P(l) ≈ 0, 05. Таким образом, использование выражения (17) также возможно, но в данном примере оно оказалось менее точным. Впоследствии целесообразно проводить проверку гипотез аналогичным методом, особенно в тех случаях, когда вследствие технологического воздействия на борную нить меняется асимметрия экспериментального распределения.

Выбрав наиболее достоверное (теоретическое) описание интегральной вероятности разрушения (16), найдем аналитическое выражение дифференциальной вероятности разрушения, используя следующее соотношение:

                                         (19)

Аналитическая функция (19) должна быть нормирована по условию:

                                      (20)

что требует учета длины интервала разбиения при нанесении графика этой функции на рис. 31. Дифференцируя выражение (16), получим:

(21)

Условие нормировки требует умножения рассчитанной по формуле (21) величина на 200 (длина интервала разбиения).

Рассчитанные значения найденных по формуле (16) и (21) функций сводим в табл. 15 и строим соответствующие графики.

Для расчета дифференциальной вероятности разрушения формулу (21) удобно привести к виду:

                 (22)

где σ _s – среднее значение напряжения в s-интервале. При этом для корректного построения графика функции (21) следует найти положение максимума этой функции и значение аргумента в данной точке

Приравнивая к нулю производную величины , получаем:

                                       (23)

Таблица 15

Сводная таблица результатов эксперимента и расчета

№	Середина интервала, МПа	Дифференциальная вероятность		Интегральная вероятность
		Эксперимент	Теория	Эксперимент	Теория
1	2300	0, 021	0, 006	0, 021	0, 005
2	2500	0	0, 015	0, 021	0, 015
3	2700	0, 021	0, 035	0, 042	0, 038
4	2900	0, 042	0, 075	0, 083	0, 091
5	3100	0, 115	0, 142	0, 198	0, 197
6	3300	0, 188	0, 225	0, 385	0, 381
7	3500	0, 323	0, 263	0, 708	0, 632
8	3700	0, 229	0, 183	0, 938	0, 865
9	3900	0, 063	0, 052	1	0, 979

 

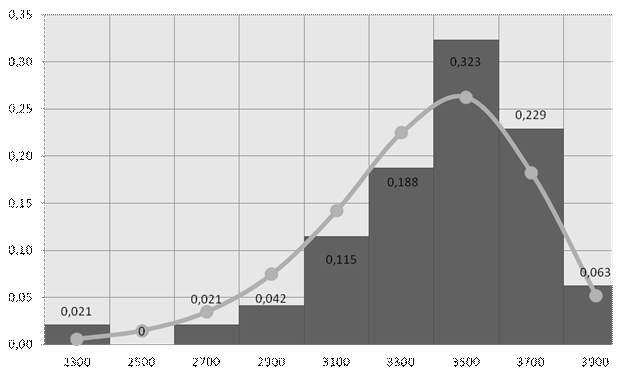
а) дифференциальная вероятность разрушения нити

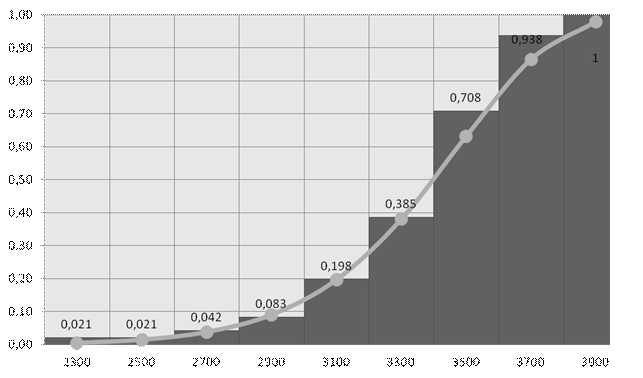
б) интегральная вероятность разрушения нити

Рис. 32. Экспериментальные зависимости вероятностей разрушения и их аналитические описания

 

Вычисление моды распределения по формуле (23) показывает, что экспериментальное среднее значение распределения, т.е. наиболее вероятное значение прочности волокна, которым следует воспользоваться при подготовке базы данных прочности

Следует заметить, что значение моды распределения  МПа и экспериментальное среднее значение распределения  МПа достаточно близки друг к другу.

Из формулы (14) и концепции слабейшего звена следует, что при испытаниях двух групп отрезком одного и того же волокна на различной базовой длине, при равной вероятности выживания (равной функции надежности ) зависимость средней прочности монофиламента от выбираемой базы испытаний должны иметь вид:

                                                  (24)

т.е., если экспериментально определена средняя прочность монофиламента на одной базе, то эта же характеристика может быть спрогнозирована для любой другой базовой длины образца. Эта зависимость подтверждена экспериментальными данными (рис. 33, рис. 34). В двойных логарифмических координатах тангенс угла наклона прямой равен β. Таким образом, модель (14) содержит в себе информацию о средней прочности волокна на любой базе испытаний. В качестве такой базы может быть и расчетная критическая длина l _кр, т.е. та минимальная длина отрезка монофиламента, на которой он может быть разрушен растяжением в композите. Следует заметить, что хотя по определению критическая длина l _кр зависит только от прочности связи по границам волокно-матрица и паспортных характеристик армирующего наполнителя, но, как это видно на рис. 33 и рис. 34, технологический режим совмещения компонентов композита может существенно влиять на прогнозируемые свойства композиционного материала.

Как следует из экспериментальных данных, снижение средней прочности волокна относительно паспортного значения может быть очень значительным и поэтому может потребоваться корректировка модели (14) с учетом параметров выбираемого режима совмещения компонентов.

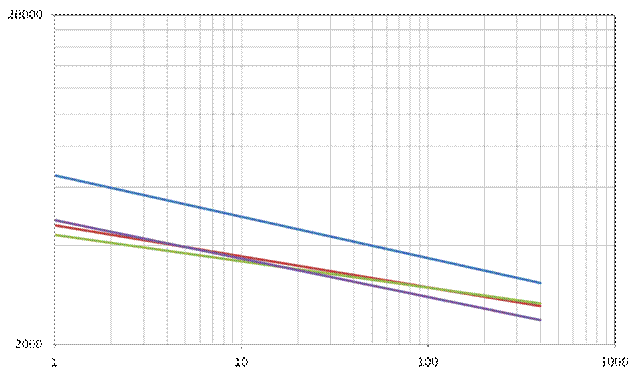
Рис. 33. Зависимость средней прочности монофиламента от базовой длины образца в двойных логарифмических координатах

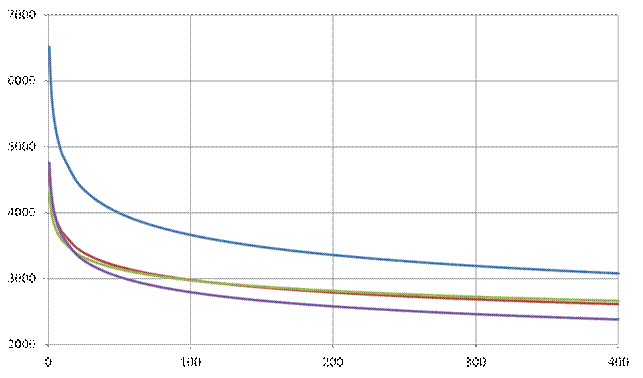
Рис. 34. Зависимость средней прочности монофиламента от базовой длины образца в обычных координатах

 

Выводы по выполненной работе сделать на основе анализа информации, представленной в табл. 16. В этой таблице результаты механических испытаний и выполненных расчетов дополнены результатами исследований поверхностей разрушения. Фрактографический анализ изломов позволяет подтвердить или опровергнуть правильность выбора вида (модели (8)) распределения. Жирным шрифтом в таблице выделены величины, которые обычно становятся паспортными характеристиками данного монофиламента и составляют базу данных об исследованном объекте (борной нити первого сорта), поставляемую поставщиком продукции. Вся информация, представленная в табл.16 составляет основу базы знаний об объекте.

 

Таблица 16

Результаты проведенного анализа

п/п	Шифр опыта	Кол-во испытаний N, шт.	b	Диаметр нити, мм	Средняя прочность, МПа	Вариации прочности, %	Значения вероятности разрушений при	Доля изломов, %; средняя прочность дефектов, МПа
								Внешние	Внутренние
1.	3-0-0	103	8	0, 1352	4360	15	42, 5	7 2940	93 4300	¾
2.	3-1-2	96	12, 5	0, 1371	3325	9, 6	40, 9	100 3180	¾	¾

Шифр опыта	Параметры и вид функции вероятности разрушения G(s)
3-0-0
3-1-2

ЛИТЕРАТУРА

1. Методические указания. Расчет и испытание на прочность в машиностроении. Методы механических испытаний. Планирование механических испытаний и статистическая обработка результатов. РД 50-398-83. М., Изд. Стандартов, 1984 г.

 

 

⇐ Предыдущая1234567

Поделиться: