Курса « Теоретической механики» Стр 1 из 9Следующая ⇒ Курса « Теоретической механики» 1.1. Сила как вектор, момент силы, главный вектор и главный момент системы сил. Роль и значение аксиом и абстракций в механике. Материальная точка. Абсолютно твердое и деформируемое твердое тело, принцип затвердевания. Аксиомы статики. Векторное представление силы. Моменты силы относительно точки и оси, связь между ними. Пара сил. Момент пары как свободный вектор. Теорема Пуансо. Приведение произвольной пространственной системы сил к одному центру. Главный вектор и главный момент. Условия эквивалентности систем сил, приложенных к твердому телу. Зависимость главного момента от выбора центра приведения, статические инварианты.  1.2. Равновесие тела и системы тел. Уравнения равновесия твердого тела. Статически определимые и статически неопределимые задачи равновесия системы твердых тел. Плоская система сил. 1.3. Трение скольжения, трения качения. Трение, основные модели, равновесие при наличии сил трения, трение скольжения и трение качения. Угол трения. 1.4. Центр тяжести. Центр параллельных сил и его свойство. Центр тяжести тела, координаты центра тяжести объёма, поверхности, линии. Дополнительные вопросы, включаемые по согласованию с выпускающими кафедрами: Частные случаи приведения системы сил. Условия равновесия при наличии сухого трения. Задача опрокидывания тела, трение качения. Глава 1. Основные положения статики. § 1. Аксиомы и принципы статики твёрдого тела. § 2. Момент силы относительно произвольного центра, оси. § 3. Пара сил и её свойства. § 4. Главный вектор и главный момент системы сил. Правило Пуансо. § 5. Приведение системы сил к простейшему виду. § 6. Уравнения равновесия тела.   Лекция 1   Вопросы для самопроверки. 1. Какую модель взаимодействия (силы) предложил Ньютон. 2. Первая аксиома статики. 3. Какие системы сил считаются эквивалентными. 4. На какие категории можно разделить все вектора, следуя физической природе векторных величин. 5. Что такое абсолютно твёрдое тело? 6. Вторая аксиома статики. 7. Третья аксиома статики. 8. Четвёртая аксиома статики. 9. В чём заключается принцип освобождаемости от связей? 10. Что такое реакции связей? Вопросы для самопроверки. 1. Напишите векторную формулу момента силы относительно точки. 2. Чему равен модуль момента силы относительно точки? 3. Прочтите ещё раз определение момента силы относительно точки. 4. Что такое момент силы относительно оси? 5. Как определяется знак момента силы относительно оси? 6. Когда момент силы относительно оси равен нулю? 7. Связь между моментом силы относительно оси и проекцией вектора момента силы на ось. 8. Чему равен модуль момента сил? 9. Чему равны проекции момента сил на оси координат? 10. Необходимым и достаточным условием равновесия сходящейся системы сил   Практическое занятие 1 Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На примерах 1.1–1.8 показаны правила замены связей реакциями сил, расположенных в плоскости.     а – тело весом G на гладкой поверхности; б – действие поверхности заменено реакцией – силой R; в – в точке А связь «опорная точка» или ребро; г – реакции направлены перпендикулярно опираемой или опирающейся плоскостям   Пример 1.1   Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (пример 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (пример 1.2).     а – балка висит на двух тросах; б – действие тросов заменено силами Т1 и Т2; в – связь «идеальный стержень»; г – связь «идеальная нить»   Пример 1.2   Шарнирно-неподвижная опора может изображаться по-разному (пример 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (пример 1.3, в), либо двумя силами, например, XA и YA (рисунок 1.3, г).     пример 1.3   Всегда можно перейти от R и α к XA и YA (и наоборот):   X A = Rcosα; Y A = Rsinα;   Шарнирно-подвижная опора (пример 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (пример 1.4, б).   Пример 1.4   Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (пример 1.5, б), их действие заменено силами XA , YA и RB . Пример 1.5   Соединение стержня и втулки в плоскости (пример 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы RD и MD момента. Пример 1.6   На примере 1.7, а изображена скользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент MC (пример 1.7, б).   Пример 1.7 Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA ) и момент ΜA (пример 1.8). Пример 1.8 На примерах 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями. Шарнирно-неподвижная опора, или сферический шарнир (пример 1.9, а), заменена системой сил (пример 1.9, б) XA , YA и ZA , т.е. силой, неизвестной по величине и направлению.   Пример 1.9   На примере 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA , YA , ZA и XB , ZB (пример 1.10, б).     Пример 1.10   На примерах 1.11 и 1.12 приведены примеры замены различных связей их реакциями.                     Пример 1.11       Задача. Задача.  Два абсолютно жестких стержня АВ и АС соединены шарниром в точке А и прикреплены к полу шарнирами В и С, образуя с полом соответственно углы 45° и 60° (рис. а). К валику шар­нира А подвешен на нерастяжимой нити груз Д вес которого 100н. Определить усилия, возникающие в стержнях АВ и АС. Весом стержней пренебречь. Решение. Для определения усилий в стержнях АВ и АС следует рассмотреть равновесие шарнира А. Однако непосредственно приступить к исследованию равновесия узла А невозможно, так как они находятся в равновесии под действием трех неизвестных сил: реакций  стержней АВ и АС и реакции нити AD. Поэтому для определения реакции нити предварительно рассмотрим равновесие груза D. Груз  D находится в равновесии под действием двух сил: веса Р и  и реакции  нити Т. Эти силы направлены в противоположные стороны (рис б) Учитывая условие равновесия груза, получим, что Т=Р=100н. реакция нити Т, направленная по вертикали  вниз (на основании закона равенства действия и противодействия). Реакции Тв и Тс стержней АВ и АС направлены вдоль стержней на рис. б эти три силы изображены приложенными в шарнире А (в общем случае трудно заранее указать, направлены ли силы Тв и Тс вдоль стержней вверх или вниз; это будет уточ­нено в ходе последующего решения задачи). . При равновесии шар­нира  А равнодействующая этих сил должна быть равна нулю, следовательно, силы Т, Тв и Тс образуют замк­нутый силовой треугольник. Построение силового тре­угольника (рис г) начнем с силы Т, известной по ве­личине и по направлению. Взяв произвольную точку О, приложим к ней силу Т. Затем, проведя через начало и конец силы Т прямые OL и SK, соответственно параллельные стержням АС и АВ, получим в пересечении третью вершину Q сило­вого треугольника OSQ. Изобразив на сторонах треугольника SQ и QO стрелки так, чтобы сумма трех сил Т, Тв и Тс равнялась нулю (в каждой из вершин силового треугольника OSQ должен быть расположен конец только одной из трех сил),.-получим направления реакций Тв и Тс. При­менив теорему синусов, получим Подставив численные значения, находим: Тв= 51,8н,  Тс = 13,2н.   Задача. Консольная балка AD весом Р=4т лежит на двух опорах В и D, причем опора В расположена на катках. На конце А к балке приложена вертикальная сосредоточенная сила F=8 т. На участке CD на балке находится равномерно распреде­ленная нагрузка интенсивности q= 0,5 т/м (интенсивностью называется величина силы, действующей на единицу длины). На участке АВ и балке приложена пара сил с моментом m = 6 тм. Определить опорные, реакции в В и D. Размеры указаны на ри­сунке. Решение. Рассмотрим равновесие балки A, на балку, действуют активные силы: вес балки Р, приложенный в её середине, сила F, равнодействующая распределенной нагрузки Q=q×CD=1т и пара сил с моментом m. Применив закон освобождаемости от связей, направим опорные реакции вверх Rb и Rd. В этом случае не только сумма всех сил должна равняться нулю, но и момент всех сил относительно выбранного центра должен быть равен нулю. Составим уравнения равновесия     Считая АВ=ВС=СD=2м, находим Rb=13.75т,  Rd=-0.75т. Отрицательное значение реакции  указывает, что направление  Rd противоположно выбранному. Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 2.10;2.30; 2.39;2.48. В качестве «помощника» рекомендуем «решебник»  М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах» , том1.   Лекция 2 Пара сил и её свойства. Рассмотрим две силы и , равные по величине и направленные в противоположные стороны, но действующие на тело не по одной прямой A B O α (рис. 6)(1). Сумма этих двух сил равна нулю, а момент? Рис 6                              h   или . Момент таких двух сил не зависит от выбранного центра, то есть вектор  является свободным: его можно переносить как угодно в пространстве, не изменяя его величины и направления(2). Кратчайшее расстояние между силами h называют плечом пары сил. Численно момент пары равен     (1.2) Перечислим основные свойства пары сил  как свободного вектора: Пару сил можно переносить в плоскости действия, пару сил можно переносить в плоскость параллельной исходной(3). Из формулы (1.2) следует, что, оставляя неизменным один из сомножителей, можно менять два остальные, сохраняя при этом значение момента пары: так, например, оставляя неизменным угол α, можно пропорционально изменить величины АВ и F(4). Совокупность пар, как угодно расположенных в пространстве, статически эквивалентна одной паре с моментом, равным векторной сумме моментов слагаемых пар. Это обозначает: чтобы сложить моменты нескольких пар, надо сложить векторно их моменты по правилу параллелограмма или векторного многоугольника(5). Здесь следует отметить, что, если две пары имеют одинаковый момент, нельзя говорить, что они равны, их действие на тело статически эквивалентно. Пара сил, вообще  говоря, является искусственным элементом, так как подобрать равными и параллельными две силы можно только с точностью измеряющих эти величины  приборов, но введение её как элемента момента силы будет полезно при дальнейшем изложении материала. Вопросы для самопроверки. 1. Что такое пара сил? 2. Почему момент пары сил свободный вектор? 3. Можно ли пару сил переносить в другую плоскость? 4. Можно ли менять параметры пары сил, если да, то как? 5. Как сложить действие нескольких пар?   Вопросы для самопроверки. 1. Что такое главный вектор системы сил? 2. Что такое главный момент системы сил? 3. Сформулируйте сами основную теорему статики, теорему Пуансо. 4. Как зависит главный момент сситстемы сил от центра приведения? 5. Какие статические инварианты Вам известны?   Вопросы для самопроверки. 1. К чему приводится система сил, если главный момент перпендикулярен главному вектору? 2. Что такое динама (или динамический винт)? 3. Как привести систему к двум непересекающимся силам? 4. К чему приводится плоская система сил? 5. К чему приводится система параллельных сил? 6. К чему приводится сходящаяся система сил? Практическое занятие 2 1. Чему равен момент силы F с проекциями на оси декартовой системы координат (1,2,3) относительно оси Oy, если координаты точки ее приложения (0,1,5) .  В нашем случае Мх=-7, Му=5, Мz=-1. 2. Чему равен момент системы сил с проекциями главного вектора ( 1,2,3 ) и проекциями главного момента относительно начала координат (3,2,1) относительно нового центра с координатами (0,2,4).     3. Р F О А В ά β Чему равен момент силы Р=10 н и F=15н    относительно оси 0Z , перпендикулярной плоскости рисунка, если ОА= 0.1м, АВ=0.15м Углы ά и β равны соответственно π/6 и π/4. Все силы лежат в плоскости чертежа.     3. Приведите указанную на рисунке систему сил к силе и паре. Равные силы направлены по диагоналям граней кубика со стороной b. Проекции главного вектора У Х Z Проекции главного момента Квадратная крышка ABCD открыта на угол α=π/3 и удерживается в этом положении стержнем СЕ. Чему равны проекции силы F на оси OX , OY и Оz?  Сила F направлена по линии ВD. X Y Z A B D F E α Крышка ABCD открыта на угол α=π/6 и удерживается в этом положении стержнем СЕ. Отношение АВ/ВС=3/4 Чему равен момент силы относительно оси OZ? Сила F направлена по линии ВD. Чтобы найти момент силы F, необходимо найти её проекции на оси координат. Спроектируем силу F на стороны крышки: на ВС и АD. Диагональ ВD прямоугольника АВСD является гипотенузой прямоугольного треугольника АВD с отношением сторон АВ:АD:ВD=3:4:5 («арабский треугольник»). Тогда проекция силы F на ось ОY равна  ,   а проекция на АВ будет  . Проекция  лежит в плоскости XYZ и направлена от В к А, следовательно . Координаты точки приложения силы  равны . Далее можно сосчитать проекции момента силы  по формуле задачи 1. Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 7.1;7.4. В качестве «помощника» рекомендуем «решебник»  М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах» , том1. Лекция 3 Уравнения равновесия тела.   Будем считать, что если взаимное положение тел и их положение относительно выбранной неподвижной системы координат остаётся неизменным, то тело или система тел находятся в равновесии. В п.4 предыдущего параграфа сказано, что произвольная система сил может быть приведена к двум непересекающимся силам. Пусть ≠0, ≠0, но при этом тело находится в равновесии. Но согласно 2-ой аксиоме статики (Свободное абсолютно твердое тело под действием двух сил будет находиться в равновесии только в том случае, когда эти силы равны, по величине и направлены вдоль одной и той же прямой в противоположные стороны), необходимо чтобы эти две силы  и ( рис. 10) в сумме давали ноль. Отсюда сразу следует, что главный вектор сил равен нулю, и как следствие нулю должен быть равен и главный момент системы сил. Это необходимое условие равновесия, достаточность этого утверждения будет доказана позже. Итак, необходимым и достаточным условием равновесия тела или системы тел является равенство нулю главного вектора и главного момента системы сил (1).                                =0 =0                              (1.6) Два векторных условия (1.6) могут быть в общем случае при­ведены к шести алгебраическим уравнениям; для этого надо спроек­тировать левые части этих уравнений на три оси координат, произ­вольно выбранные в пространстве. Тогда при принятых обозначениях будем иметь следующие шесть уравнений (2):                                                 которые выражают следующее положение: при равновесии твердого тела под действием пространственной системы сил суммы проекций приложенных сил на оси координат и суммы моментов приложенных сил относительно осей координат равны нулю. При изучении условий равновесия данного тела оно рассматривается как свободное, для чего оно мысленно выделяется из общей цепи взаимодействующих тел. Действие других тел заменяется реакциями связей, поэтому в уравнения равновесия входят как задаваемые (активные) силы так и реакции связей. В отдельных частных случаях некоторые из этих шести урав­нений могут выполняться тождественно; при этом число уравнений равновесия уменьшается. Отметим важнейшие из этих частных случаев. 1. Сходящаяся система сил (3). Выбирая точку, в которой сходятся линии действия сил, за центр моментов, заметим, что уравнения моментов тождественно обратятся в нуль, так как линии действия сил пересекут оси координат, число уравнений равновесия сокращается до трех уравнений проекций на оси координат. 2. Плоская система сил (4). Расположим ось OZ перпендику­лярно к плоскости действия сил. Тогда три уравнения тождественно обратятся в ноль (см. п.1 предыдущего параграфа) и станутся три уравнения                                                                                        3. Равновесие системы тел (плоская система сил). В статике часто встречаются задачи, в которых число неизвестных реакций больше чем три. В этом случае для решения задачи необходимо учитывать наличие внутренних шарниров ( не путать с реакциями шарниров). Если Ν-К=3, где N-число неизвестных реакций, К-число внутренних шарниров, то задача называется статически определимой и может быть решена методами статики твёрдого тела (5). Для статически неопределимых задач надо записать дополнительные условия, чтобы число неизвестных уравнений было равно числу неизвестных. Поскольку этот параграф является основным в разделе статика, уместно в лекции рассмотреть подробно два примера.   ЗАДАЧА 1.Однородная балка веса 600ни длины 4м опирается одним концом на гладкий пол, а промежуточной точкой С – на вертикальную стенку высотой 3м, образуя с вертикалью угол π/6. Балка удерживается в таком положении веревкой АВ, протянутой по полу. Пренебрегая трением, определить натяжение веревки Т, реакции вертикальной стенки Rс и пола Nв.   Решение. 1. Необходимо освободиться от связей, заменив их соответствующими реакциями. На рис. все эти три реакции показаны (Т,Nв,Rс). Выбрать систему координат. Следует направить оси так, чтобы наибольшее число сил проектировалось в «полный рост». Выбрать начало координат в точке, относительно которой уравнение моментов запишется в наиболее простом виде. В нашей задаче все эти 3 условия выполнены. Так как имеем дело с плоской задачей, необходимо записать три уравнения равновесия. Имеем 3 уравнения с тремя неизвестными. Из последнего уравнения определяем Rс=100 =173.2н. Из первого получаем Т=150, и, наконец, Nв=513.4н.     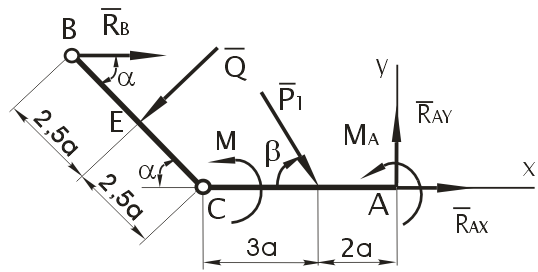ЗАДАЧА 2. Механическая система состоит из 2-х балок ВС и АС, соединённых между собой цилиндрическим шарниром С. В точке А  балка СА закрепляется в вертикальной стенке с помощью жёсткой заделки, в точке В – с помощью невесомого стержня ВD. Система нагружена равномерно распределённой нагрузкой интенсивностью q, парой сил с моментом М и силой Р1. Определить реакции в точках А, В, С. Весом балок и трением в шарнирах пренебречь. Дано: a P КЕ P1 𝛽 M q α м н м н град нм н/м град 1,2 0 0 1,5 30 1 4,8 60 a P KE Pa b M q al В последней строке стоят имена данных для символьных вычислений.   Составить уравнения для частей и целой конструкции в виде BC CA ABC
Vx=0	Vy=0	Mc=0	Vx=0	Vy=0	Mc=0	Vx=0	Vy=0	Mc=0

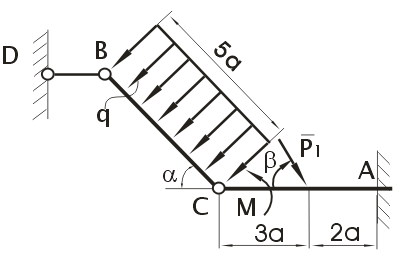
Рис. 1

Рассмотрим равновесие каждого из тел системы.

Балка ВС (рис. 2)

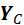
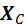
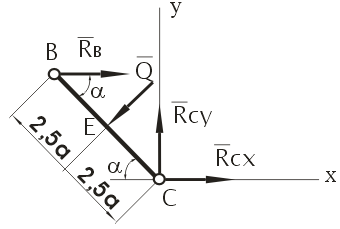
Рис. 2

 

На балку действуют:

- равнодействующая Q равномерно распределённой нагрузки в точке Е; модуль силы равен Q = 5q×a = 5 × 4,8 × 1,2 = 28,80; (Н)

- реакцию невесомого стержня X_B и  составляющие X_C, Y_C реакции цилиндрического шарнира направим положительно.

Поскольку балка ВС находится в равновесии, то выполняются следующие условия:

1) V_X = X_B + X_C – Q × sin a = 0,

2) V_Y = Y_C – Q × cos a = 0,

3) M_C= Q × 2,5a – X_B× 5a× sin a = 0. 

    Балка СА (рис. 3)

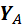
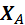
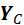
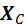
Рис. 3

На балку действуют: сила Р₁ и момент М;

в точке А – реакции  X_A, Y_A  и момент М_А жёсткой заделки направим положительно в точке С – реакции X_C, Y_C цилиндрического шарнира согласно третьему закону Ньютона направим противоположно соответствующим реакциям балки ВС.

Поскольку балка ВС находится в равновесии, то выполняются следующие условия:

4) V_X = X_A – X_C + P₁×cosb = 0,

5) V_Y = Y_A – Y_C – P₁× sin b = 0,

6) M_C= M + M_A – (P₁× sin b) × 3a + Y_A× 5a = 0.

Проверка

    Для проверки полученных результатов необходимо составить уравнения равновесия всей системы и подставить туда решения. Если суммы обратятся в ноль, то решение верно.

 

7) V_X = X_B – Q × sin a+X_A + P₁×cosb= 0 ?,

8) V_Y = Y_A – Q × cos a – P₁× sin b = 0 ?,

9) M_C= Q× 2,5a – X_B× 5a×sina+M + M_A – (P₁×sinb) × 3a + Y_A× 5a = 0

 Вопросы для самопроверки.

1. Необходимое и достаточное условие равновесия твердого тела (векторная форма).

2. Необходимое и достаточное условие равновесия твердого тела (в проекциях на оси координат).

3. Напишите уравнения равновесия сходящейся системы сил.

4. Напишите уравнения равновесия плоской системы сил.

5. Что такое статически определимая задача (на примере плоской задачи)

 

Практическое занятие 3

 

m

F

К

m

F

C

D

α

β

Е

А

В

Пример 1. Условия задачи

Параллелепипед нагружен силой F и моментом m.

1. Докажите, что они не уравновешены.

2. Обозначьте вершины, углы и оси.

3. Поставьте определимые связи:

4. сферический и цилиндрический шарниры, стержень на двух шарнирах.

5. Запишите уравнения равновесия тела

 

К

x

XA

y

YA

ZA

z

m

F

А

В

C

D

E

α

β

Решение.

1. Сила и момент не могут быть уравновешенными, поскольку в точке приложения силы главный вектор системы равен силе F, а главный момент - моменту m и оба не равны нулю.

2. Обозначим углы α и β и вершины А,В,Е, в которых будем ставить связи. Добавим обозначения вершин С и D для обозначения размеров тела.

3.

К

XE

ZE

x

XA

y

YA

ZA

z

S

m

F

А

В

C

D

E

α

β

Поставим определимые связи. Начнем с сферического шарнира в вершине А. Поскольку в нем возникает наибольшее число неизвестных (3), то разумно здесь выбрать начало координат. Реакция шарнира направлена произвольно и может проходить через точки В и Е остальных связей.

 В точке Е поставим цилиндрический шарнир. Чтобы связи остались определимыми, нужно направить его ось так, чтобы его реакция не могла пройти через вершину А. Реакция цилиндрического шарнира направлена произвольно в плоскости, перпендикулярной оси шарнира. Поэтому его ось не может быть перпендикулярной прямой АЕ. Иначе связи станут избыточными в направлении АВ и недостаточными для поворота вокруг оси, перпендикулярной АЕ. Направим ось цилиндрического шарнира вдоль оси у.

Осталось поставить стержень на шарнирах в вершине В. Его нельзя направить в плоскости АВЕ. Иначе он будет избыточным в своем направлении и не удержит тело от поворота вокруг АЕ. Направим стержень вдоль оси у.

4. Геометрический способ

 Уравнения проекций не вызывают затруднений

                                               V_x: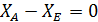

                                                  V_y: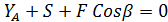

                            V_z: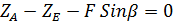

 

При вычислении моментов сил пользуемся простым алгоритмом.

Сначала интересуемся, не равен ли момент силы нулю (сила параллельна или пересекает ось). Например, F пересекает ось у.

 

Если ответ отрицательный, то смотрим, не перпендикулярна ли сила оси. Тогда момент ищется по формуле, например

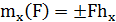
    Знак лучше выбирать, представив, куда движется винт под действием силы. Если винт движется по оси,   то плюс, иначе – минус. 

Для поиска плеча 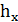 пользуемся правилом трех направлений.  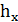должно быть перпендикулярно и F и х.

Если сила направлена по отношению к оси произвольно, то следует разложить ее на составляющие вдоль осей. Для составляющих пользуемся вторым случаем. 

                                 Mx: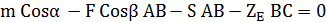           

                                       My: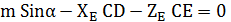  

                                       Mz: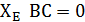   

 

Рассмотрим второй пример.

Однородная прямоугольная плита веса Q = 8кН , прикрепленная к стенке при помощи сферического шарнира А и цилиндрического шарнира В, удерживается в горизонтальном положении при помощи невесомого стержня, шарнирно закрепленного по концам. К плите приложена сила F=15 кН и пара сил с моментом M = 5 кНм . Определить опорные реакции и усилие в стержне.

Решение

Составим расчетную схему задачи, изобразив плиту под действием активной нагрузки и реакций связей (сила тяжести Q приложена в точке пересечения диагоналей плиты). Систему координат выберем таким образом, чтобы наибольшее число неизвестных реакций было параллельно координатным осям и пересекало их (это значительно упрощает уравнения равновесия). Для удобства решения задачи векторы F и M разложены на составляющие, параллельные координатным осям:

F1=F·cosα, F2=F·sinα M1=M·cosα, M2=M·sinα

где (см. рис.)

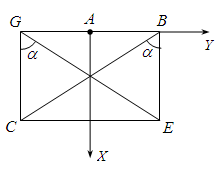
Таким образом получаем:

F1=15·0,6=9 кН, F2=15·0,8=12 кН M1=5·0,6=3 кНм, M2=5·0,8=4 кНм

Неизвестное усилие S, направленное вдоль стержня CD, также удобнее представить в виде двух составляющих: S1=S·cos30o=0,866·S, S3=S·sin30o=0,5·S (а).

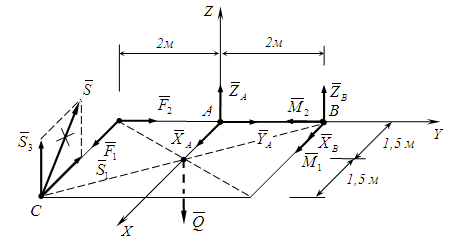Расчетная схема

Составим уравнения равновесия

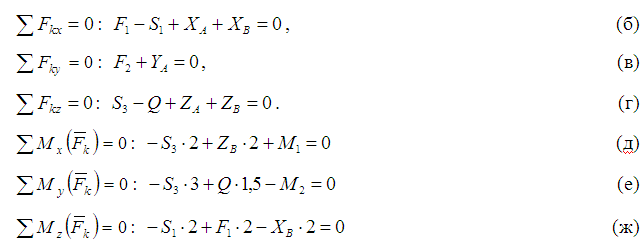
Решая систему уравнений (б) – (ж), подставив в нее предварительно выражения (а), получим:

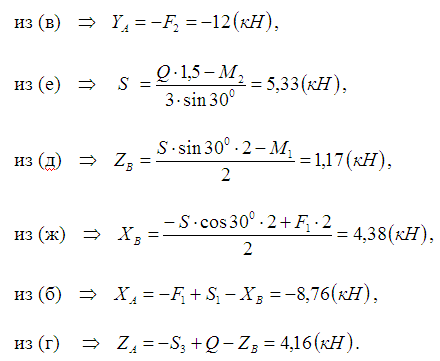
Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 4.10;4.11;4.28;4.38;4.41;8.13;8.25;8.26;8.28;8.29.

В качестве «помощника» рекомендуем «решебник»

 М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах» , том1.

 

Если в планах кафедр предусмотрена курсовая работа по статике, предлагаются задания по теме «равновесие системы тел».

Пример решения такого задания прилагается.

 

В предлагаемом примере необходимо определить четыре неизвестные реакции: три в заделке А и одна реакция в шарнире В. Но уравнений можно записать только три (см. 4). Наличие шарнира  С позволяет решить эту задачу , если мы рассмотрим отдельно два тела, но при этом введем еще две реакции Хс и Yс.

 

 

 

  

 

Первоначально у нас было 4 неизвестных реакций и три уравнения, теперь мы имеем 6 неизвестных реакций , но, для каждого из тел теперь можем записать по три уравнения, то есть имеем 6 уравнений для 6 неизвестных реакций. Ниже записаны 6 уравнений статики, решение которых предлагается выполнить самостоятельно.

Полученные результаты, если нет ответов, необходимо проверить. Для этого предлагается сосчитать главный вектор активных сил (задаваемые силы) и главный вектор сил реакций, а также момент задаваемых сил и момент реакций относительно выбранного центра. Полученные значения должны отличаться только знаком ( с заданной точностью).

 

 

Расчётные задания для самостоятельной работы.

F

P

C

A

d

q

a

b

M

b

a

B

1.Найти опорные реакции в опорах A и B и реакции в шарнире C.
a (м)	b(м)	d(м)	α α	β	P (кн)	F (кн)	q (кн/м)	M (кн*м)
2	3	4	0	0	10	6	2	3

M

q

b

F

C

d/2

a

B

P

A

b

d/2

aff

1.Найти опорные реакции в опорах A и B и реакции в шарнире C.
a (м)	b(м)	d(м)	α	β	P (кн)	F (кн)	q(кн/м)	M(кн*м)
3	3	4	60	30	10	6	2	1

 

a

d/2

F

A

q

a

b

C

P

B

M

b

d/2

1.Найти опорные реакции в опорах A и B и реакции в шарнире C.
a (м)	b(м)	d(м)	α	β	P (кн)	F (кн)	q(кн/м)	M(кн*м)
2	3	4	45	0	10	6	2	1

F

M

d/2

A

b

P

b

a

B

C

a

d/2

1.Найти опорные реакции в опорах A и B и реакции в шарнире C.
a (м)	b(м)	d(м)	α	β	P (кн)	F (кн)	q (кн/м)	M (кн*м)
2	3	4	0	30	10	6	2	1

P

F

A

C

B

a

b

d

D

aff

βff

q

M

1.Найти опорные реакции в опорах A и B и реакции в D и C.
a (м)	b(м)	d(м)	α	β	P (кн)	F (кн)	q(кн/м)	M(кн*м)
4	3	3	30	0	10	6	2	4

A

F

a

B

a

P

q

d

b

d

M

b

C

α

1.Найти реакции в опорах A, В и реакции в скользящей заделке C.
a (м)	b(м)	d(м)	α	β	P (кн)	F (кн)	q (кн/м)	M (кн*м)
3	2	3	30	-30	10	12	2	3

Лекция 4

Глава2

Центр параллельных сил.

 

Р

О

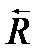
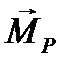
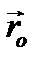
Рис 11

Система параллельных сил, как было указано выше, приводится к равнодействующей (1). Докажем теорему Вариньона: если система сил приводится к равнодействующей, то момент этой равнодействующей, относительно произвольной точки равен геометрической сумме моментов сил относительно этой точки (2). Действительно, зависимость главного момента от центра приведения задаётся формулой (1.4)

Выберем точку О на линии действия равнодействующей. Тогда 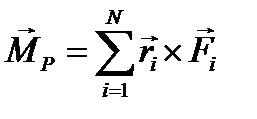, но =0, как момент равнодействующей относительно точки, лежащей на линии её действия, и тогда

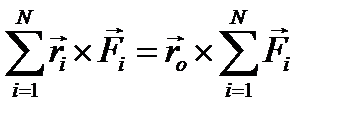                                   (1.9)

Пусть для определённости все силы параллельны оси OZ , в этом случае можно записать 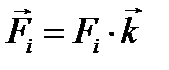, а формулу (1.9) переписать в виде

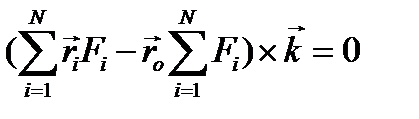                                                                (1.10)

Для выполнения условия (1.10) должно быть: или выражение в скобках равно нулю, либо выражение в скобках параллельно вектору 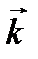, но мы выбрали направление OZ произвольно, следовательно, нулю должно быть равно выражение в скобках, из которого и получаем выражение для центра параллельных сил (3)      

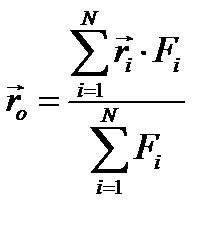                                                                                  (1.11)

Центр параллельных сил всегда находится на линии равнодействующей, но это особая точка. Если все силы повернуть на один и тот же угол, не меняя их точек приложения, то выражение в скобках формулы (12) и модуль равнодействующей не изменится, но сама равнодействующая повернётся на тот же угол вокруг центра параллельных сил (4). В проекциях на оси декартовой системы координат формула (1.11) записывается в виде 

 

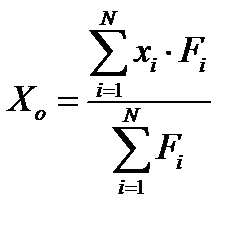
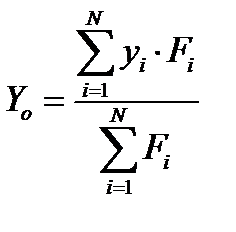
                               (1.12)

Вопросы самопроверки.

1. Докажите, что система параллельных сил приводится к равнодействующей.

2. Сформулируйте теорему Вариньона.

3. Напишите формулу центра параллельных сил.

4. Какое свойство центра параллельных сил Вам известно?

§ 2. Центр тяжести, методы определения координат центра тяжести.

Понятие центра параллельных сил весьма полезно для нахождения центра тяжести тела, центра объёма, сечения. Рассмотрим случай силы тяжести. (При небольших размерах тела во всех технических приложениях можно считать силы тяжести отдельных частиц тела системой параллельных сил. Угол между направлениями сил тяжести двух точек, расположенных на поверхности Земли на расстоянии 1 км друг от друга по меридиану, равен 32"). Элементарные объёмы тела весом 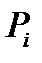 каждый, образуют систему параллельных сил, и для них справедливы формулы (14), если силу  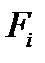заменить на 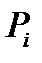.Но эти формулы являются приближёнными, так как значения координат  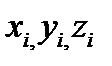определяются с точностью до размеров кубиков 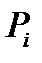. Чем меньше размеры кубиков, тем меньшую ошибку сделаем, определяя центр тяжести по формулам (1.12). Поэтому устремим число N  к бесконечности. Предел такого рода есть определённый интеграл.

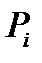
О

X

Y

Z

Рис 12

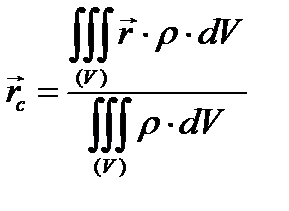                              (1.13)

Формула (1.13) определяет координаты центра сил тяжести частиц тела, или, спроектировав векторную запись на соответствующие оси, координаты центра тяжести тела. В этих формулах величина ρ(xyz) есть вес единицы объема, т. е, удельный вес неоднородного тела. В случае однородного тела величина ρ постоянна (не зависит от координат) и может быть вынесена за знак суммы в числителе и знаменателе, а затем сокращена. Таким образом, получаем формулы для координат центра тяжести однородного тела(1)

                                     

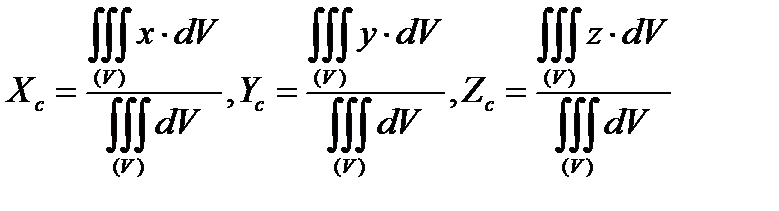
Так как в последних формулах фигурируют только геометрические величины, то говорят, что они определяют центр объема. Если параллельные силы непрерывно распределены по некоторой поверхности Ѕ однородного тела, то в формуле (1.13) надо положить  dV=HdS где H- сила, отнесенная к единице площади по­верхности (напряжение), а dS —элементарные площадки, на которые мысленно разбита поверхность. Получаем

 

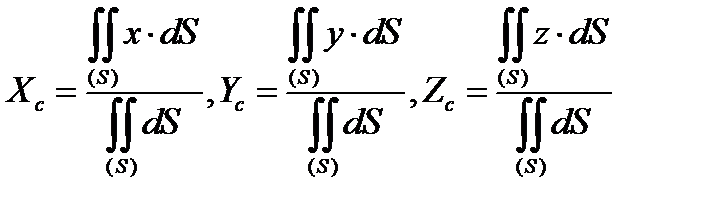                                         (1.14)

Параллельные силы могут быть также непрерывно распределены вдоль некоторой линии, как, например, силы тяжести, приложенные к тонкой проволоке, ось которой представляет данную линию. Полагаем 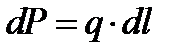 и при однородном материале и постоянном поперечном сечении, q-вес единицы длины (погонный вес) проволоки будет постоянным, и мы получаем фор­мулы для координат центра тяжести однородной линии:

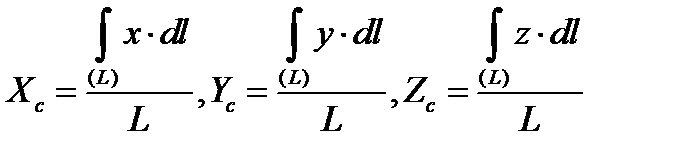                                    (1.15)

Фактическое разыскание координат центра тяжести объема, поверхности или линии требует применения методов интегрального исчисления. В практических приложениях часто прихо­дится иметь дело с телами или фигурами, составленными из нескольких тел, фигур, имеющих известные геометрические формы, положение центров тяжести которых известно. Для таких тел положение центра тяжести может быть определено без вычисления интегралов.

1. Если однородное тело имеет ось симметрии или плоскость симметрии, центр объёма, фигуры, будет находиться на этой оси. Если однородное тело имеет плоскость симметрии, то центр объёма будет находиться в этой плоскости. При наличии двух плоскостей симметрии центр тяжести будет находиться на линии пересечения этих плоскостей (2).

2. Представим себе, что однородный объём V может быть разбит на несколько объёмов 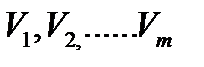, координаты центров которых известны. Тогда нетрудно найти и координаты центра объема V. В самом деле, имеем (для ):

                            

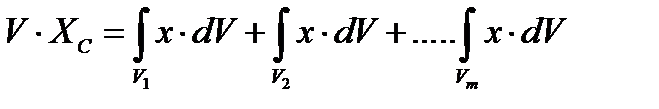
и аналогичные формулы можно написать для 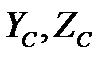, тогда

                    

                                (1.16)

Аналогичные формулы могут быть написаны в случае поверх­ности плоской фигуры, а также и для неоднородных тел, поверхно­стей и линий (3).

В случае, если для составления объема V некоторые из слагае­мых объемов нужно вычесть (тело с отверстиями), можно пользо­ваться теми же формулами (1.16), если условиться слагаемые, соот­ветствующие отбрасываемым объемам, брать с отрицательными знаками (4). Рассмотрим пример.

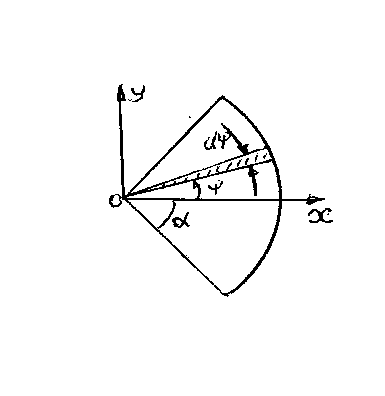Центр сечения. Дан сектор радиуса R, с углом 2α. Ось ОХ является осью симметрии, поэтому 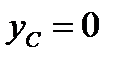. Выделим в заданном секторе бесконечно малый сектор с площадью 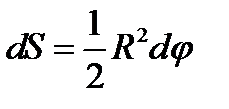, центр выделенного сектора 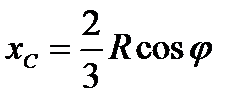. Подставляя полученные формулы в (1.14), получим

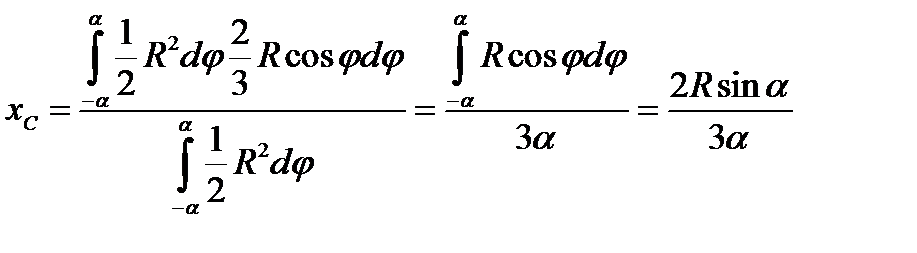
Для  - .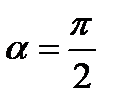

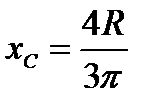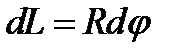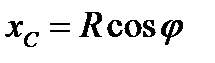Если необходимо определить центр дуги, то , а . Подставляя полученные формулы в (1.15), имеем 

.

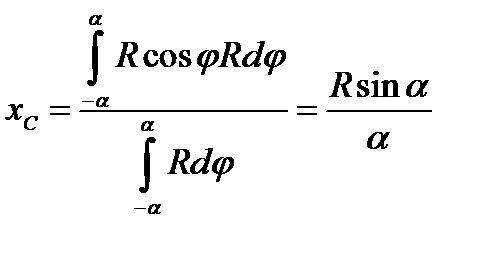Для  - .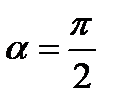

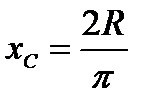Определение центров тяжести линий и площадей во многих случаях может быть облегчено, если пользоваться теоремами Паппа-Гульдина. Эти теоремы гласят:

1. Боковая поверхность тела вращения, описанная дугой плоской кривой, вращающейся вокруг оси, расположенной в плоскости кри­вой и ее не пересекающей, равна длине дуги, умноженной на длину окружности, описываемой центром тяжести дуги. Это первая теорема. Действительно, для дуги 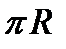 имеем 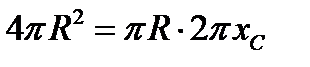, откуда следует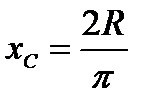

2. Объём тела вращения, описанного плоской фигурой, вращающейся вокруг оси, расположенной в плоскости фигуры и не пересекающей её контура, равен произведению площади фигуры на длину окружности, описываемой её центром тяжести. Это вторая теорема.

Действительно, для сектора  получаем , откуда следует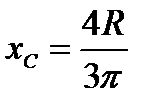         

Вопросы для самопроверки.

1. Напишите формулы центра тяжести тела.

2. Где находится центр тяжести тел имеющих какую либо симметрию.

3. Как определяется центр тяжести составного тела или составной фигуры.

4. Как учесть пустоты и отверстия в теле при нахождении центра тяжести.

 

Практическое занятие 4

Задача 1. Найти координаты центра тяжести тела, имеющего вид стула, состоящего из стержней одинаковой длины и веса. Длина стержня 44см.

Решение. В проекциях на оси декартовой системы координат формула (1.11) записывается в виде 

 

                      

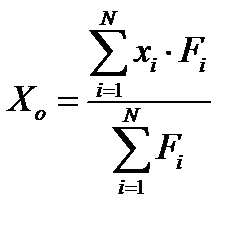
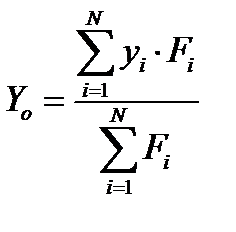
Здесь F=mg(вес стержня), поэтому написанную формулу после сокращений можно переписать в виде            

 

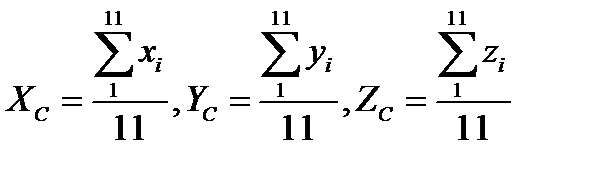
В выбранной системе координат будем иметь

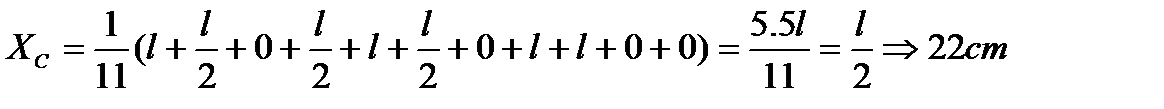
Этот результат очевидный, центра тяжести тела должен находится в плоскости симметрии тела.

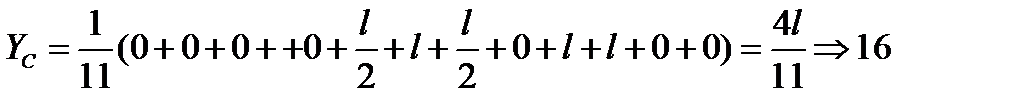
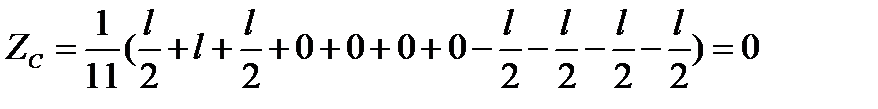
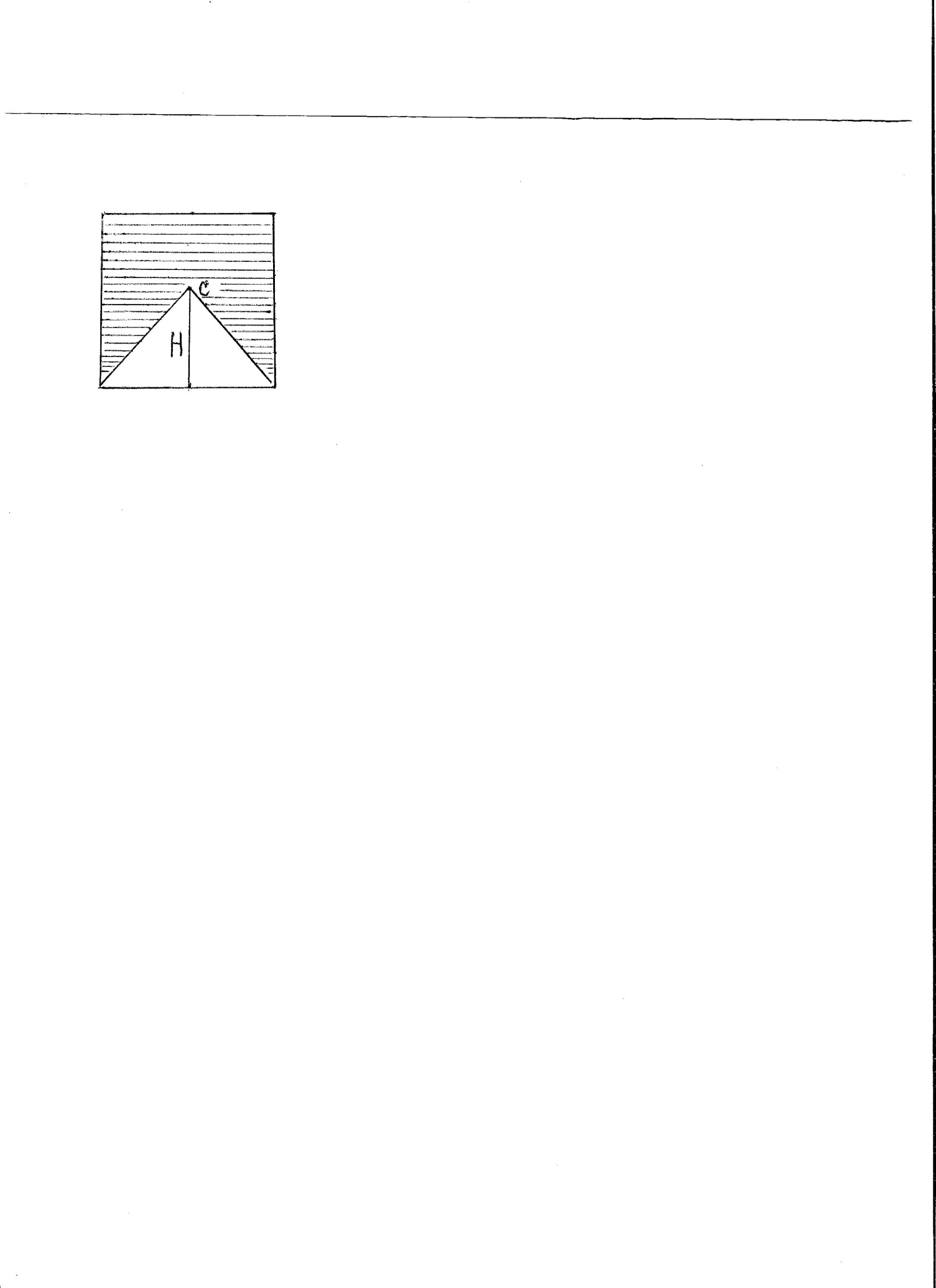
Задача 2. Дан квадрат со стороной b. Найти внутри него такую точку С, чтобы она была центром тяжести площади, если из квадрата вырезать равнобедренный треугольник.

Решение задачи сводится к определению высоты H равнобедренного треугольника. .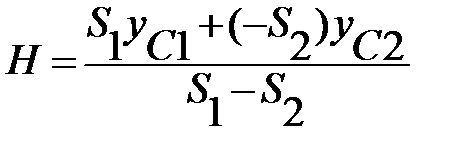

Здесь S1 – площадь квадрата, S2- площадь треугольника, взятого со знаком минус (дырка), Y1 и Y2-соответственно, координаты центров тяжести. Подставляя их значения, имеем

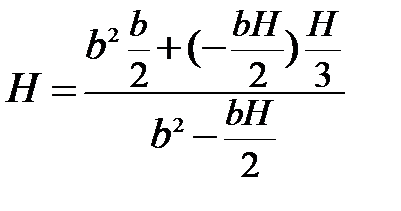
Для определения высоты H получаем квадратное уравнение ,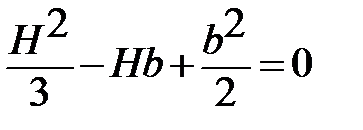

решая которое получаем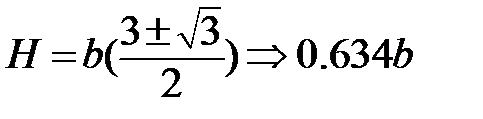

Задача 3.

Найти предельную высоту H цилиндра, при которой тело, состоящее из цилиндра плотности ρ1, полушара плотности ρ2 и одинакового радиуса r , теряет устойчивость в положении равновесия, когда оно опирается на гладкую горизонтальную поверхность. Расстояние центра тяжести однородного полушара от его основания равно (3/8)r.

Реакция пола R всегда проходит через точку О (центр полушара). На рис В показано, что если центр тяжести тела находится в точке С1, возникает пара сил, опрокидывающая тело, если центр тяжести тела находится в точке С2, возникает пара сил, стремящаяся вернуть тело в исходное положение. Отсюда следует, что центр тяжести всего тела должен быть выше центра полушара или в предельном случае совпадать с ним. Запишем формулу для центра тяжести

 

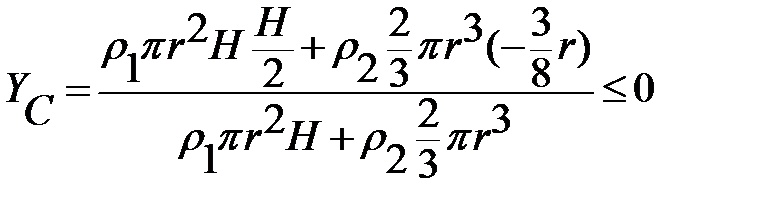
или после сокращений .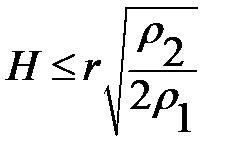

Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 9.9;9.12;9.13;9.20;9.26

В качестве «помощника» рекомендуем «решебник»

 М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах» , том1.

Лекция 5

Глава 3.

Вопросы для самопроверки.

1. Перечислите основные положения модели сухого трения.

2. Что такое угол трения?

3. Какому соотношению отвечает сила трения при равновесии?

4. Что такое явление заклинивания или самоторможения механизма?

Вопросы для самопроверки.

1. Как может двигаться тело при нарушении равновесия в зависимости от его размеров и коэффициента трения?

2. От чего зависит момент трения качения?

3. Что такое коэффициент трения качения?

 

Практическое занятие 5.

Задача 1. Груз Р удерживается в равновесии конструкцией, состоящей из 2 стержней, как показано на чертеже. Две муфты могут скользить по вертикальной стойке, коэффициента трения скольжения муфты по стойке f. Размеры указаны на рис. Определить условие самоторможения конструкции.

Решение.

Для плоской системы сил составим 3 уравнения равновесия.

 

 

Из первого и третьего уравнения имеем

 тогда

Здесь F1=F2 –есть силы трения, и так как получаем

или окончательно                 .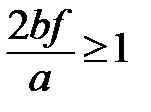

Задача 2. Чему равна сила трения в указанном примере, если вес груза 100 н, угол наклона плоскости π/6, сила Q=65 н, а коэффициент трения скольжения f=0.3?

 

Решение. Спроектируем все силы оси: параллельно N

 и перпендикулярно N

.

Знак  у силы трения означает, что направление силы трения не определено. Из второго уравнения находим

н, следовательно, сила трения направлена вниз. Но , а . Ответ F=15н.

Задача 3 . Ящик веса Р стоит на шероховатой горизонтальной плоскости с коэффициентом трения f. Определить, под каким углом α надо приложить силу Q, и величину этой силы при условии сдвинуть ящик при наименьшей величине Q.

 

Решение. Для сходящейся системы сил надо написать 2 уравнения равновесия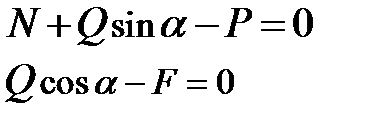

Из первого уравнения получаем . Подстановка   во второе уравнение приводит к следующему выражению для силы Q.                              

Для определения Qмин напишем функцию

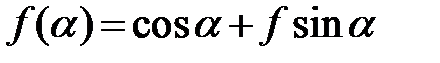
и исследуем ее на экстремум. Для этого возьмем первую и вторую производные по α.

Из равенства нулю первой производной получаем                     , где φ-угол трения. Вторая производная отрицательна, следовательно функция f(α) имеет максимум, а сила Q –минимум.

Задача 4.

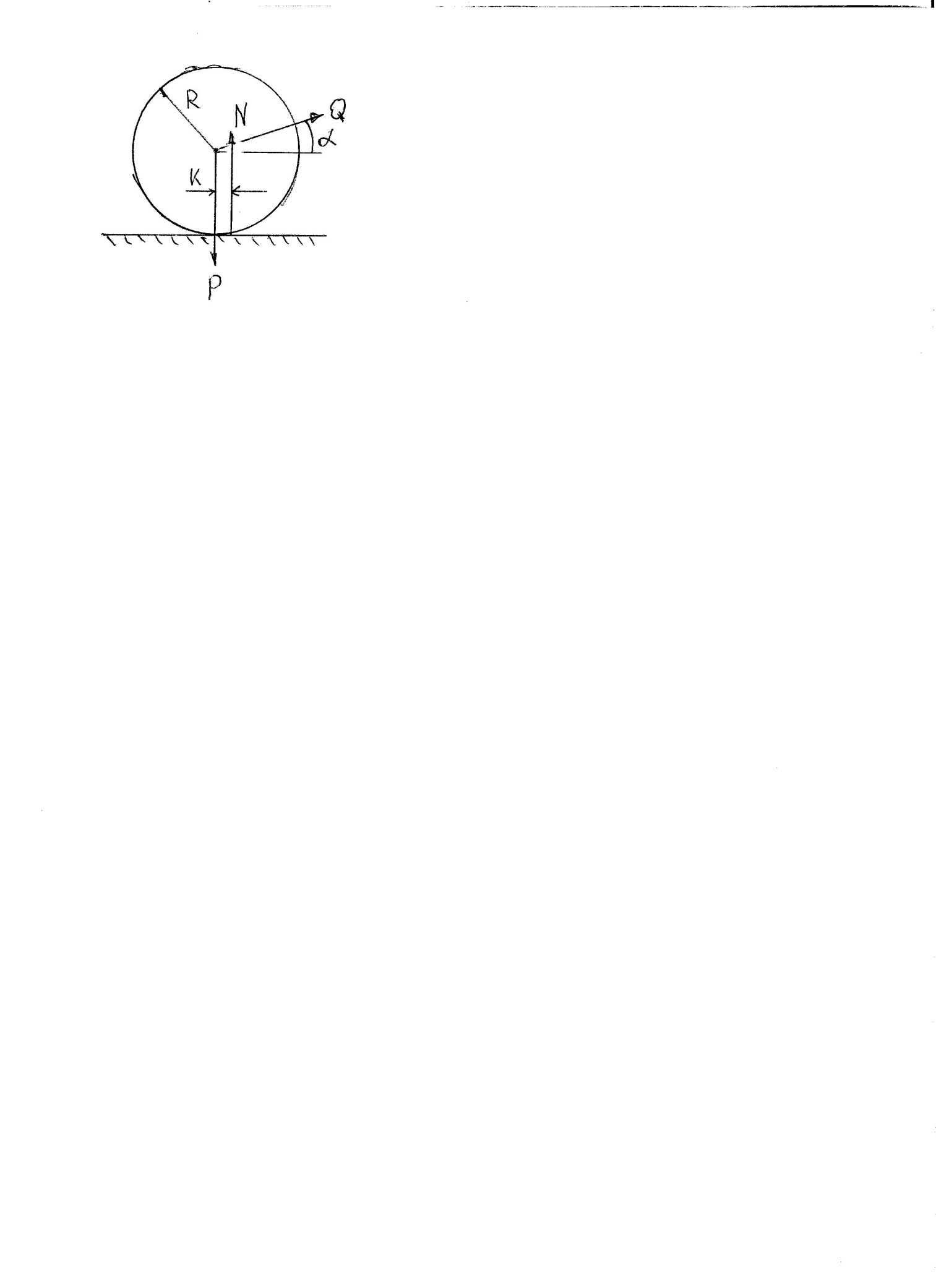Определить силу Q , необходимую для равномерного качения цилиндрического катка радиуса 30см и веса 300н по горизонтальной плоскости, если коэффициент трения качения

k=0.5см, а угол α=π/6.

Решение. Составим уравнения равновесия цилиндра

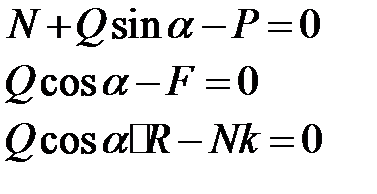
Сила F (сила трения) не указана на рисунке, хотя она есть и направлена влево параллельно плоскости. Из первого уравнения определяем нормальную реакцию N и используя два условия , получаем

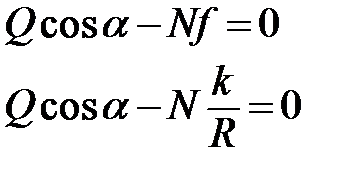
Если , то цилиндр будет скользить и не вращаться, что не соответствует условию задачи, следовательно, из второго уравнения имеем

н

Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 5.6;5.17;5.26;5.306

В качестве «помощника» рекомендуем «решебник»

 М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах», том1.

Вопросы для самопроверки:

Предварительные замечания. В предлагаемых вопросах есть как теоретические вопросы так и задачи. Цифры и геометрия рисунков могут быть изменены.

Что такое момент силы относительно точки?

 

Чему равен момент силы F с проекциями на оси декартовой системы координат (1,2,3) относительно оси Oy, если координаты точки ее приложения (0,1,5) (варианты Ox, Oz)?

q0

Чему равен момент заделки в указанном примере, если длина стержня равна 0.6м, а q0=2 кн/м ?

 

Напишите условия равновесия сходящейся системы сил в векторной форме, а также в проекциях на оси декартовой системы координат.

 

Р

F

О

А

В

ά

β

Что такое пара сил, чему равен ее момент?

 

Как зависит главный момент от выбора центра приведения,

 

7. Чему равен момент силы Р=10 н и F=15н относительно оси 0Z , перпендикулярной плоскости рисунка, если ОА= 0.1м, АВ=0.15м Углы ά и β равны соответственно π/6 и π/4. Все силы лежат в плоскости чертежа. Определите главный вектор заданных сил.

 

 

8. Какие уравнения равновесия необходимо записать для плоской системы сил, если все силы расположены в

X

Y

Z

A

B

D

F

E

α

плоскости XOY ( варианты XOZ, YOZ )?

 

9. Крышка ABCD открыта на угол α=π/3 и удерживается в этом положении стержнем СЕ. Отношение АВ/ВС=3/4 Чему равны проекции силы F на указанные оси координат?

Чему равен момент силы F относительно оси OX (OZ)? АВ=L, сила F направлена по линии ВD.

 

10. Какие уравнения равновесия необходимо записать для системы сил, параллельных оси OY (варианты OX,OZ ) ?

 

11. Сформулируйте теорему Пуансо.

 

12. Какие статические инварианты Вам известны,?

 

13. В каких случаях система сил приводится к равнодействующей?

У

Х

Z

 

14. Приведите указанную на рисунке систему сил к простейшему виду. Равные силы направлены по диагоналям граней кубика со стороной b.

15. В каких случаях момент силы относительно оси равен нулю ?

 

16. Сформулируйте теорему Вариньона.

 

17. Векторная формула центра параллельных сил.

18. Докажите, что система параллельных сил приводится к равнодействующей.

 

19. Векторная формула центра тяжести, прокомментируйте введенные обозначения.

 

20. Где находится центр тяжести указанной фигуры, состоящей из квадрата и равностороннего треугольника со стороной в?

 

21. Где находится центр тяжести указанной фигуры, состоящей из квадрата со стороной в и прямоугольного треугольника с углом при вершине 30˚ ?

 

22. Где находится центр квадрата, из которого вырезан полукруг. Длина стороны квадрата 2 R , радиус полукруга R, центр тяжести полукруга находится на расстоянии 4R/3π от диаметра.

F

α

23. Чему равна сила трения в указанном примере, если вес груза 100 н, угол наклона плоскости π/4, сила F=50н, а коэффициент трения скольжения f=0.4?

курса « Теоретической механики»

1.1. Сила как вектор, момент силы, главный вектор и главный момент системы сил.

Роль и значение аксиом и абстракций в механике. Материальная точка. Абсолютно твердое и деформируемое твердое тело, принцип затвердевания. Аксиомы статики. Векторное представление силы. Моменты силы относительно точки и оси, связь между ними. Пара сил. Момент пары как свободный вектор. Теорема Пуансо. Приведение произвольной пространственной системы сил к одному центру. Главный вектор и главный момент. Условия эквивалентности систем сил, приложенных к твердому телу. Зависимость главного момента от выбора центра приведения, статические инварианты.

 1.2. Равновесие тела и системы тел.

Уравнения равновесия твердого тела. Статически определимые и статически неопределимые задачи равновесия системы твердых тел. Плоская система сил.

1.3. Трение скольжения, трения качения.

Трение, основные модели, равновесие при наличии сил трения, трение скольжения и трение качения. Угол трения.

1.4. Центр тяжести.

Центр параллельных сил и его свойство. Центр тяжести тела, координаты центра тяжести объёма, поверхности, линии.

Дополнительные вопросы, включаемые по согласованию с выпускающими кафедрами: Частные случаи приведения системы сил. Условия равновесия при наличии сухого трения. Задача опрокидывания тела, трение качения.

Глава 1.

123456789Следующая ⇒

Поделиться: