
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Приведение системы сил к простейшему виду.
 системы и приложенной в произвольном центре приве системы и приложенной в произвольном центре приве
дения О, и одной паре с моментом
Рис 8 заменять эквивалентной ей сово
 и момента и момента  , прилоложенных в точке О. При изменении положения центра приведения О главный вектор , прилоложенных в точке О. При изменении положения центра приведения О главный вектор  будет сохранять величину и направление, а главный момент будет сохранять величину и направление, а главный момент  будет изменяться. Докажем, что если главный вектор отличен от нуля и перпендикулярен к главному моменту, то система сил приводится к одной силе, которую в этом случае будем называть равнодействующей будет изменяться. Докажем, что если главный вектор отличен от нуля и перпендикулярен к главному моменту, то система сил приводится к одной силе, которую в этом случае будем называть равнодействующей 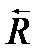 (рис.8). Главный момент (рис.8). Главный момент  можно представить парой сил ( можно представить парой сил ( 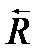 , , 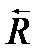 ) с плечом ) с плечом 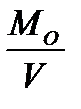 , тогда силы , тогда силы 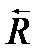 и главный вектор и главный вектор  образуют систему двух сил эквивалентную нулю, которую можно отбросить. Останется одна сила образуют систему двух сил эквивалентную нулю, которую можно отбросить. Останется одна сила 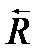 , действующая вдоль прямой, параллельной главному вектору и проходящей на расстоянии h= , действующая вдоль прямой, параллельной главному вектору и проходящей на расстоянии h= 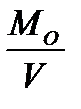 от плоскости, образуемой векторами от плоскости, образуемой векторами  и и  (1). Рассмотренный случай показывает, что если с самого начала выбрать центр приведения на прямой L, то систему сил сразу бы привели к равнодействующей, главный момент был бы равен нулю. Теперь докажем, что если главный вектор отличен от нуля и не перпендикулярен к главному моменту, то за центр приведения может быть выбрана такая точка О*, что главный момент относительно этой точки и главный вектор расположатся на одной прямой. Для доказательства разложим момент (1). Рассмотренный случай показывает, что если с самого начала выбрать центр приведения на прямой L, то систему сил сразу бы привели к равнодействующей, главный момент был бы равен нулю. Теперь докажем, что если главный вектор отличен от нуля и не перпендикулярен к главному моменту, то за центр приведения может быть выбрана такая точка О*, что главный момент относительно этой точки и главный вектор расположатся на одной прямой. Для доказательства разложим момент  на две составляющие- одну на две составляющие- одну 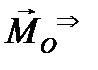 , направленную вдоль главного вектора, и другую , направленную вдоль главного вектора, и другую 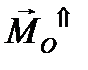 - перпендикулярную к главному вектору. Тем самым пара сил - перпендикулярную к главному вектору. Тем самым пара сил  раскладывается на две пары с моментами: раскладывается на две пары с моментами: 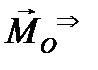 и и 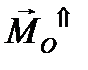 , причем плоскость первой пары перпендикулярна к , причем плоскость первой пары перпендикулярна к  , тогда плоскость второй пары, перпендикулярная к вектору , тогда плоскость второй пары, перпендикулярная к вектору 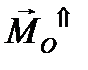 (рис 9) содержит вектор (рис 9) содержит вектор  . Совокупность пары с моментом . Совокупность пары с моментом 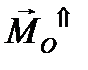 и силы и силы  образует систему сил, которая может быть сведена к одной силе (рис.8) , проходящей через точку О*. Таким образом (рис 9), совокупность главного вектора образует систему сил, которая может быть сведена к одной силе (рис.8) , проходящей через точку О*. Таким образом (рис 9), совокупность главного вектора  и главного момента и главного момента  в точке О сведена к силе в точке О сведена к силе  , проходящей через точку О*, и паре с моментом параллельным этой прямой , проходящей через точку О*, и паре с моментом параллельным этой прямой 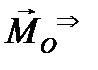 , что и требовалось доказать. Совокупность силы и пары, плоскость которой перпендикулярна к линии действия силы, называется динамой (2)(рис.10). , что и требовалось доказать. Совокупность силы и пары, плоскость которой перпендикулярна к линии действия силы, называется динамой (2)(рис.10). Пару сил можно представить двумя равными по величине силами (
 , откуда следует (рис.10), что совокупность главного вектора , откуда следует (рис.10), что совокупность главного вектора  и главного момента и главного момента  в точке О, может быть сведена к двум непересекающимся силам в точке О, может быть сведена к двум непересекающимся силам 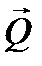 и и  (3). (3).
Рассмотрим некоторые случаи приведения системы сил. 1. Плоская система сил (4). Пусть для определённости все силы находятся в плоскости OXY. Тогда в самом общем случае Главный вектор не равен нулю, главный момент не равен нулю, их скалярное произведение равно нулю, действительно
следовательно, главный вектор перпендикулярен главному моменту: плоская система сил приводится к равнодействующей . 2. Система параллельных сил (5). Пусть для определённости все силы параллельны оси OZ. Тогда в самом общем случае Здесь также главный вектор не равен нулю, главный момент не равен нулю, а их скалярное произведение равно нулю, действительно
следовательно, и этом случае главный вектор перпендикулярен главному моменту: система параллельных сил приводится к равнодействующей . В частном случае, если 1) Пусть 2) 3) 4) Вопросы для самопроверки. 1. К чему приводится система сил, если главный момент перпендикулярен главному вектору? 2. Что такое динама (или динамический винт)? 3. Как привести систему к двум непересекающимся силам? 4. К чему приводится плоская система сил? 5. К чему приводится система параллельных сил? 6. К чему приводится сходящаяся система сил? Практическое занятие 2 1. Чему равен момент силы F с проекциями на оси декартовой системы координат (1,2,3) относительно оси Oy, если координаты точки ее приложения (0,1,5) .
В нашем случае Мх=-7, Му=5, Мz=-1. 2. Чему равен момент системы сил с проекциями главного вектора ( 1,2,3 ) и проекциями главного момента относительно начала координат (3,2,1) относительно нового центра с координатами (0,2,4).
3.
3. Приведите указанную на рисунке систему сил к силе и паре. Равные силы направлены по диагоналям граней кубика со стороной b. Проекции главного вектора
Проекции главного момента
Чтобы найти момент силы F, необходимо найти её проекции на оси координат. Спроектируем силу F на стороны крышки: на ВС и АD. Диагональ ВD прямоугольника АВСD является гипотенузой прямоугольного треугольника АВD с отношением сторон АВ:АD:ВD=3:4:5 («арабский треугольник»). Тогда проекция силы F на ось ОY равна
Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 7.1;7.4. В качестве «помощника» рекомендуем «решебник» М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах» , том1. Лекция 3 |
Последнее изменение этой страницы: 2019-06-09; Просмотров: 190; Нарушение авторского права страницы