
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Центр параллельных сил и центр тяжести.
§ 1. Центр параллельных сил § 2. Центр тяжести. Методы определения координат центра тяжести. Центр параллельных сил.
Выберем точку О на линии действия равнодействующей. Тогда Пусть для определённости все силы параллельны оси OZ , в этом случае можно записать Для выполнения условия (1.10) должно быть: или выражение в скобках равно нулю, либо выражение в скобках параллельно вектору Центр параллельных сил всегда находится на линии равнодействующей, но это особая точка. Если все силы повернуть на один и тот же угол, не меняя их точек приложения, то выражение в скобках формулы (12) и модуль равнодействующей не изменится, но сама равнодействующая повернётся на тот же угол вокруг центра параллельных сил (4). В проекциях на оси декартовой системы координат формула (1.11) записывается в виде
Вопросы самопроверки. 1. Докажите, что система параллельных сил приводится к равнодействующей. 2. Сформулируйте теорему Вариньона. 3. Напишите формулу центра параллельных сил. 4. Какое свойство центра параллельных сил Вам известно? § 2. Центр тяжести, методы определения координат центра тяжести. Понятие центра параллельных сил весьма полезно для нахождения центра тяжести тела, центра объёма, сечения. Рассмотрим случай силы тяжести. (При небольших размерах тела во всех технических приложениях можно считать силы тяжести отдельных частиц тела системой параллельных сил. Угол между направлениями сил тяжести двух точек, расположенных на поверхности Земли на расстоянии 1 км друг от друга по меридиану, равен 32"). Элементарные объёмы тела весом
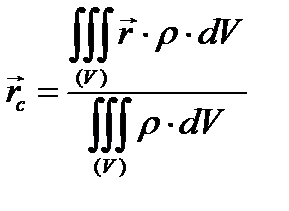 (1.13) (1.13)
Формула (1.13) определяет координаты центра сил тяжести частиц тела, или, спроектировав векторную запись на соответствующие оси, координаты центра тяжести тела. В этих формулах величина ρ(xyz) есть вес единицы объема, т. е, удельный вес неоднородного тела. В случае однородного тела величина ρ постоянна (не зависит от координат) и может быть вынесена за знак суммы в числителе и знаменателе, а затем сокращена. Таким образом, получаем формулы для координат центра тяжести однородного тела(1) Так как в последних формулах фигурируют только геометрические величины, то говорят, что они определяют центр объема. Если параллельные силы непрерывно распределены по некоторой поверхности Ѕ однородного тела, то в формуле (1.13) надо положить dV=HdS где H- сила, отнесенная к единице площади поверхности (напряжение), а dS —элементарные площадки, на которые мысленно разбита поверхность. Получаем
Параллельные силы могут быть также непрерывно распределены вдоль некоторой линии, как, например, силы тяжести, приложенные к тонкой проволоке, ось которой представляет данную линию. Полагаем Фактическое разыскание координат центра тяжести объема, поверхности или линии требует применения методов интегрального исчисления. В практических приложениях часто приходится иметь дело с телами или фигурами, составленными из нескольких тел, фигур, имеющих известные геометрические формы, положение центров тяжести которых известно. Для таких тел положение центра тяжести может быть определено без вычисления интегралов. 1. Если однородное тело имеет ось симметрии или плоскость симметрии, центр объёма, фигуры, будет находиться на этой оси. Если однородное тело имеет плоскость симметрии, то центр объёма будет находиться в этой плоскости. При наличии двух плоскостей симметрии центр тяжести будет находиться на линии пересечения этих плоскостей (2). 2. Представим себе, что однородный объём V может быть разбит на несколько объёмов и аналогичные формулы можно написать для
Аналогичные формулы могут быть написаны в случае поверхности плоской фигуры, а также и для неоднородных тел, поверхностей и линий (3). В случае, если для составления объема V некоторые из слагаемых объемов нужно вычесть (тело с отверстиями), можно пользоваться теми же формулами (1.16), если условиться слагаемые, соответствующие отбрасываемым объемам, брать с отрицательными знаками (4). Рассмотрим пример.
Для Если необходимо определить центр дуги, то
Для Определение центров тяжести линий и площадей во многих случаях может быть облегчено, если пользоваться теоремами Паппа-Гульдина. Эти теоремы гласят: 1. Боковая поверхность тела вращения, описанная дугой плоской кривой, вращающейся вокруг оси, расположенной в плоскости кривой и ее не пересекающей, равна длине дуги, умноженной на длину окружности, описываемой центром тяжести дуги. Это первая теорема. Действительно, для дуги 2. Объём тела вращения, описанного плоской фигурой, вращающейся вокруг оси, расположенной в плоскости фигуры и не пересекающей её контура, равен произведению площади фигуры на длину окружности, описываемой её центром тяжести. Это вторая теорема. Действительно, для сектора Вопросы для самопроверки. 1. Напишите формулы центра тяжести тела. 2. Где находится центр тяжести тел имеющих какую либо симметрию. 3. Как определяется центр тяжести составного тела или составной фигуры. 4. Как учесть пустоты и отверстия в теле при нахождении центра тяжести.
Практическое занятие 4
Задача 1. Найти координаты центра тяжести тела, имеющего вид стула, состоящего из стержней одинаковой длины и веса. Длина стержня 44см. Решение. В проекциях на оси декартовой системы координат формула (1.11) записывается в виде
Здесь F=mg(вес стержня), поэтому написанную формулу после сокращений можно переписать в виде
В выбранной системе координат будем иметь
Этот результат очевидный, центра тяжести тела должен находится в плоскости симметрии тела.
Задача 2. Дан квадрат со стороной b. Найти внутри него такую точку С, чтобы она была центром тяжести площади, если из квадрата вырезать равнобедренный треугольник. Решение задачи сводится к определению высоты H равнобедренного треугольника. Здесь S1 – площадь квадрата, S2- площадь треугольника, взятого со знаком минус (дырка), Y1 и Y2-соответственно, координаты центров тяжести. Подставляя их значения, имеем
Для определения высоты H получаем квадратное уравнение решая которое получаем Задача 3.
Найти предельную высоту H цилиндра, при которой тело, состоящее из цилиндра плотности ρ1, полушара плотности ρ2 и одинакового радиуса r , теряет устойчивость в положении равновесия, когда оно опирается на гладкую горизонтальную поверхность. Расстояние центра тяжести однородного полушара от его основания равно (3/8)r. Реакция пола R всегда проходит через точку О (центр полушара). На рис В показано, что если центр тяжести тела находится в точке С1, возникает пара сил, опрокидывающая тело, если центр тяжести тела находится в точке С2, возникает пара сил, стремящаяся вернуть тело в исходное положение. Отсюда следует, что центр тяжести всего тела должен быть выше центра полушара или в предельном случае совпадать с ним. Запишем формулу для центра тяжести
или после сокращений Для самостоятельной подготовки к контрольной работе рекомендуется решить следующие задачи из задачника И.В. Мещерского «Сборник задач по теоретической механике» : 9.9;9.12;9.13;9.20;9.26 В качестве «помощника» рекомендуем «решебник» М.И. Бать, Г.И. Джанелидзе, А.С.Кельзон «Теоретическая механика в примерах и задачах» , том1. Лекция 5 Глава 3. |
Последнее изменение этой страницы: 2019-06-09; Просмотров: 323; Нарушение авторского права страницы