КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ

Стр 1 из 9Следующая ⇒

КазНУ им. Аль-Фараби

МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ

КУРСОВАЯ РАБОТА

по дисциплине

Системный анализ и задачи

Математического программирования

на тему:

Методы экономического программирования.

выполнил: студент 2 курса,

группы ИС 04 03 А

Гришко Михаил

проверил: к. ф.-м. н., доцент кафедры ИС Тургенбаева Г.А.

Алматы 2005г.

Содержание.

1. Введение…………………………………………………………………………………………..3

2. Теоретическая часть……………………………………………………………………………...4

2.1. Математическое представление и структура экономических показателей………………4

2.2. Предварительный анализ и обработка временных рядов…………………………………5

2.2.1. Выявление и устранение аномальных значений……………………………………..5

2.2.2. Выявление тренда……………………………………………………………………...5

2.2.3. Определение сезонных колебаний……………………………………………………7

2.2.4. Сглаживание временных рядов……………………………………………………….9

2.3. Расчет показателей динамики развития экономических процессов…………………….10

2.4. Прогнозирование экономических показателей…………………………………………...13

2.4.1. Трендовые модели на основе кривых роста………………………………………...13

2.4.1.1. Выбор типа кривых роста…………………………………………………….14

2.4.1.2. Методы определения параметров отбора кривых роста…………………...17

2.4.1.3. Определение адекватности трендовой модели…………………………….18

2.4.1.4. Точность прогноза трендовой модели……………………………………....20

2.4.1.5. Верификация прогноза……………………………………………………….22

2.4.2. Адаптивные модели прогнозирования………………………………………………23

3. Практическая часть……………………………………………………………………………..25

3.1. Постановка задачи…………………………………………………………………………..25

3.2. Построение модели…………………………………………………………………………25

3.3. Адекватность и точность…………………………………………………………………..28

3.3.1. Случайность колебаний уровней остаточной последовательности……………….28

3.3.2. Соответствие распределения случайной компоненты нормальному закону распределения……………………………………………………………………….28

3.3.3. Равенство математического ожидания случайной компоненты нулю……………28

3.3.4. Независимость значения уровней случайной компоненты………………………..29

3.3.5. Точность прогноза построенной трендовой модели……………………………….29

4. Заключение……………………………………………………………………………………...30

5. Список использованных источников………………………………………………………….31
1. Введение.

Предсказание временных рядов – необходимый элемент любой инвестиционной деятельности. Сама идея инвестиций – вложение денег сейчас с целью получения дохода в будущем – основывается на идее прогнозирования будущего. Соответственно, предсказание финансовых временных рядов лежит в основе деятельности всей индустрии инвестиций – всех бирж и внебиржевых систем торговли ценными бумагами.

Прогнозирование экономических показателей основано на идее экстраполяции. Под экстраполяцией обычно понимают распространение закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределы. В более широком смысле слова ее рассматривают как получение представлений о будущем на основе информации, относящейся к прошлому и настоящему. В процессе построения прогнозных моделей в их структуру иногда закладываются элементы будущего предполагаемого состояния объекта или явления, но в целом эти модели отражают закономерности, наблюдаемые в прошлом и настоящем, т.е. прогноз возможен лишь относительно таких объектов и явлений, которые в значительной степени детерминируются прошлым и настоящим.

Цель данного курсового проекта – рассмотреть основные методы экономического прогнозирования, а также решить поставленную задачу с помощью трендовых моделей на основе кривых роста.

Теоретическая часть

Выявление тренда.

Для определения наличия трендав исходном временном ряду применяется несколько методов:

Прогнозирование экономических показателей.

При экстраполяционном прогнозировании экономической динамики на основе временных рядов с использованием трендовых моделей выполняются следующие основные этапы:

1) предварительный анализ данных;

2) формирование набора моделей (например, набора кривых роста), называемых функциями-кандидатами;

3) численное оценивание параметров моделей;

4) определение адекватности моделей;

5) оценка точности адекватных моделей;

6) выбор лучшей модели;

7) получение точечного и интервального прогнозов;

8) верификация прогноза.

Прогноз на основании трендовых моделей (кривых роста) содержит два элемента: точечный и интервальный прогнозы. Точечный прогноз - это прогноз, которым называется единственное значение прогнозируемого показателя. Это значение определяется подстановкой в уравнение выбранной кривой роста величины времени t, соответствующей периоду упреждения: t = n + 1; t = n + 2 и т.д. Такой прогноз называется точечным, так как на графике его можно изобразить в виде точки. Очевидно, что точное совпадение фактических данных в будущем и прогностических точечных оценок маловероятно. Поэтому точечный прогноз должен сопровождаться двусторонними границами, т.е. указанием интервала значений, в котором с достаточной долей уверенности можно ожидать появления прогнозируемой величины. Установление такого интервала называется интервальным прогнозом.

Интервальный прогноз на базе трендовых моделей осуществляется путем расчета доверительного интервала - такого интервала, в котором с определенной вероятностью можно ожидать появления фактического значения прогнозируемого экономического показателя. Расчет доверительных интервалов при прогнозировании с использованием кривых роста опирается на выводы и формулы теории регрессий. Методы, разработанные для статистических совокупностей, позволяют определить доверительный интервал, зависящий от стандартной ошибки оценки прогнозируемого показателя, от времени упреждения прогноза, от количества уровней во временном ряду и от уровня значимости (ошибки) прогноза.

Трендовые модели на основе кривых роста.

Основная цель создания трендовых моделей экономической динамики - на их основе сделать прогноз о развитии изучаемого процесса на предстоящий промежуток времени. Прогнозирование на основе временного ряда экономических показателей относится к одномерным методам прогнозирования, базирующимся на экстраполяции, т.е. на продлении на будущее тенденции, наблюдавшейся в прошлом. При таком подходе предполагается, что прогнозируемый показатель формируется под воздействием большого количества факторов, выделить которые либо невозможно, либо по которым отсутствует информация. В этом случае ход изменения данного показателя связывают не с факторами, а с течением времени, что проявляется в образований одномерных временных рядов. Рассмотрим метод экстраполяции на основе так называемых кривых роста экономической динамики.

Использование метода экстраполяции на основе кривых роста для прогнозирования базируется на двух предположениях:

- временной ряд экономического показателя действительно имеет тренд, т.е. преобладающую тенденцию;

- общие условия, определявшие развитие показателя в прошлом, останутся без существенных изменений в течение периода упреждения.

Выбор типа кривых роста.

В настоящее время насчитывается большое количество типов кривых роста для экономических процессов. Наиболее часто в экономике используются полиномиальные, экспоненциальные и S-образные кривые роста. Простейшие полиномиальные кривые роста имеют вид:

(полином первой степени)

(полином второй степени)

(полином третьей степени)

и т.д.

Параметр а₁ называют линейным приростом,

параметр а₂ - ускорением роста,

параметр а₃ - изменением ускорения роста.

Для полинома первой степени характерен постоянный закон роста. Если рассчитать первые приросты по формуле u_t = y_t - y_t-i, t = 2, 3, ..., n, то они будут постоянной величиной и равны а₁.

Если первые приросты рассчитать для полинома второй степени, то они будут иметь линейную зависимость от времени и ряд из первых приростов u₂, u₃, … на графике будет представлен прямой линией. Вторые приросты для полинома второй степени будут постоянны.

Для полинома третьей степени первые приросты будут полиномами второй степени, вторые приросты будут линейной функцией времени, а третьи приросты, рассчитываемые по формуле будут постоянной величиной.

Можно отметить следующие свойства полиномиальных кривых роста:

- от полинома высокого порядка можно путем расчета последовательных разностей (приростов) перейти к полиному более низкого порядка;

- значения приростов для полиномов любого порядка не зависят от значений самой функции .

Таким образом, полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.

В отличие от использования полиномиальных кривых использование экспоненциальных кривых роста предполагает, что дальнейшее развитие зависит от достигнутого уровня, например, прирост зависит от значения функции. В экономике чаще всего применяются две разновидности экспоненциальных (показательных) кривых: простая экспонента и модифицированная экспонента.

Простая экспонента представляется в виде функции

(34)

где a и b — положительные числа, при этом если b больше единицы, то функция возрастает с ростом времени t, если b меньше единицы - функция убывает.

Модифицированная экспонента имеет вид

(35)

где постоянные величины: а меньше нуля, b положительна и меньше единицы, а константа k носит название асимптоты этой функции, т.е. значения функции неограниченно приближаются (снизу) к величине k. Могут быть другие варианты модифицированной экспоненты, но на практике наиболее часто встречается указанная выше функция.

В экономике достаточно распространены процессы, которые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу. В качестве примера можно привести процесс ввода некоторого объекта в промышленную эксплуатацию, процесс изменения спроса на товары, обладающие способностью достигать неко торого уровня насыщения, и др. Для моделирования таких процессов используются так называемые S-образные кривые роста, среди которых выделяют кривую Гомперца и логистическую кривую.

Кривая Гомперца имеет аналитическое выражение

(36)

где а, b - положительные параметры, причем b меньше единицы;

параметр k - асимптота функции.

В кривой Гомперца выделяются четыре участка: на первом - прирост функции незначителен, на втором - прирост увеличивается, на третьем участке прирост примерно постоянен, на четвертом - происходит замедление темпов прироста и функция неограниченно приближается к значению k. В результате конфигурация кривой напоминает латинскую букву S.

Логарифм данной функции является экспоненциальной кривой; логарифм отношения первого прироста к самой ординате функции - линейная функция времени. На основании кривой Гомперца описывается, например, динамика показателей уровня жизни; модификации этой кривой используются в демографии для моделирования показателей смертности и т. д.

Логистическая кривая, или кривая Перла-Рида - возрастающая функция, наиболее часто выражаемая в виде

; (37)

другие виды этой кривой:

; . (38)

где а и b — положительные параметры;

k — предельное значение функции при бесконечном возрастании времени.

Если взять производную данной функции, то можно увидеть, что скорость возрастания логистической кривой в каждый момент времени пропорциональна достигнутому уровню функции и разности между предельным значением k и достигнутым уровнем. Логарифм отношения первого прироста функции к квадрату ее значения (ординаты) есть линейная функция от времени.

Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.

Рассмотрим проблему предварительного выбора вида кривой роста для конкретного временного ряда. Допустим, имеется временной ряд y₁, y₂, …, y_n .

Для выбора вида полиномиальной кривой роста наиболее распространенным методом является метод конечных разностей (метод Тинтнера). Этот метод может быть использован для предварительного выбора полиномиальной кривой, если, во-первых, уровни временного ряда состоят только из двух компонент: тренд и случайная компонента, и, во-вторых, тренд является достаточно гладким, чтобы его можно было аппроксимировать полиномом некоторой степени.

На первом этапе этого метода вычисляются разности (приросты) до k-го порядка включительно:

;

; (39)

........

Для аппроксимации экономических процессов обычно вычисляют конечные разности до четвертого порядка.

Затем для исходного ряда и для каждого разностного ряда вычисляются дисперсии по следующим формулам:

для исходного ряда

; (40)

для разностного ряда k-го порядка (k = 1, 2, ...)

; (41)

где - биномиальный коэффициент.

Производится сравнение отклонений каждой последующей дисперсии от предыдущей, т.е. вычисляются величины

, (42)

и если для какого-либо k эта величина не превосходит некоторой наперед заданной положительной величины, т.е. дисперсии одного порядка, то степень аппроксимирующего полинома должна быть равна k - 1.

Более универсальным методом предварительного выбора кривых роста, позволяющим выбрать кривую из широкого класса кривых роста, является метод характеристик прироста. Он основан на использовании отдельных характерных свойств кривых, рассмотренных выше. При этом методе исходный временной ряд предварительно сглаживается методом простой скользящей средней. Например, для интервала сглаживания m = 3 сглаженные уровни рассчитываются по формуле

, (43)

причем чтобы не потерять первый и последний уровни, их сглаживают по формулам

, . (44)

Затем вычисляются первые средние приросты

, t = 2, 3, …, n-1; (45)

вторые средние приросты

, (46)

а также ряд производных величин, связанных с вычисленными средними приростами и сглаженными уровнями ряда:

; ; ; .

В соответствии с характером изменения средних приростов и производных показателей выбирается вид кривой роста для исходного временного ряда, при этом используется табл. 1.

Таблица 1

Выбор кривой роста в соответствии с изменением приростов и производных показателей

Показатель	Характер изменения показателя во времени	Вид кривой роста
Первый средний прирост	Примерно одинаковы	Полином первого порядка
Первый средний прирост	Изменяются линейно	Полином второго порядка
Второй средний прирост	Изменяются линейно	Полином третьего порядка
	Примерно одинаковы	Простая экспонента
	Изменяются линейно	Модифицированная экспонента
	Изменяются линейно	Кривая Гомперца
	Изменяются линейно	Логистическая кривая

На практике при предварительном выборе отбирают обычно две-три кривые роста для дальнейшего исследования и построения трендовой модели данного временного ряда.

2.4.1.2. Методы определения параметров отобранных кривых роста.

Параметры полиномиальных кривых оцениваются, как правило, методом наименьших квадратов, суть которого заключается в том, чтобы сумма квадратов отклонений фактических уровней ряда от соответствующих выровненных по кривой роста значений была наименьшей. Этот метод приводит к системе так называемых нормальных уравнений для определения неизвестных параметров отобранных кривых.

Для полинома первой степени

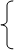система нормальных уравнений имеет вид:

(47)

;

где знак суммирования распространяется на все моменты наблюдения (все уровни) исходного временного ряда. Аналогичная система для полинома второй степени

имеет вид

, (48)

;

и т.д.

Параметры экспоненциальных и S-образных кривых находятся более сложными методами. Для простой экспоненты предварительно логарифмируют выражение по некоторому основанию (например, десятичному или натуральному):

т.е. для логарифма функции получают линейное выражение, а затем для неизвестных параметров log a и log b составляют на основе метода наименьших квадратов систему нормальных уравнений, аналогичную системе для полинома первой степени. Решая эту систему, находят логарифмы параметров, а затем и сами параметры модели.

При определении параметров кривых роста, имеющих асимптоты (модифицированная экспонента, кривая Гомперца, логистическая кривая), различают два случая. Если значение асимптоты k известно заранее, то путем несложной модификации формулы и последующего логарифмирования определение параметров сводят к решению системы нормальных уравнений, неизвестными которой являются логарифмы параметров кривой.

Если значение асимптоты заранее неизвестно, то для нахождения параметров указанных выше кривых роста используются приближенные методы: метод трех точек, метод трех сумм и др. Таким образом, при моделировании экономической динамики, заданной временным рядом, путем сглаживания исходного ряда, определения наличия тренда, отбора одной или нескольких кривых роста и определения их параметров в случае наличия тренда получают одну или несколько трендовых моделей для исходного временного ряда.

Верификация прогноза.

При экстраполяционном прогнозировании экономической динамики с использованием трендовых моделей весьма важным является заключительный этап — верификация прогноза. Верификация любых дескриптивных моделей, к которым относятся трендовые модели, сводится к сопоставлению расчетных результатов по модели с соответствующими данными действительности — массовыми фактами и закономерностями экономического развития. Верификация прогнозной модели представляет собой совокупность критериев, способов и процедур, позволяющих на основе многостороннего анализа оценивать качество получаемого прогноза. Однако чаще всего на этапе верификации в большей степени осуществляется оценка метода прогнозирования, с помощью которого был получен результат, чем оценка качества самого результата. Это связано с тем, что до сих пор не найдено эффективного подхода к оценке качества прогноза до его реализации.

Проверка точности одного прогноза недостаточна для оценки качества прогнозирования, так как она может быть результатом случайного совпадения. Наиболее простой мерой качества прогнозов при условии, что имеются данные об их реализации, является отношение числа случаев, когда фактическая реализация охватывалась интервальным прогнозом, к общему числу прогнозов. Данную меру качества прогнозов k можно вычислить по формуле

, (72)

где р — число прогнозов, подтвержденных фактическими данными;

q — число прогнозов, не подтвержденных фактическими данными.

Однако в практической работе проблему качества прогнозов чаще приходится решать, когда период упреждения еще не закончился и фактическое значение прогнозируемого показателя неизвестно. В этом случае более точной считается модель, дающая более узкие доверительные интервалы прогноза.

Практическая часть

Постановка задачи

Дан временной ряд:

t	1	2	3	4	5	6	7	8	9	10
y_t	43	47	50	48	54	57	61	59	65	62

Необходимо сделать предварительный выбор наилучшей кривой роста:

1. методом конечных разностей (Тинтнера)

2. методом характеристик прироста

Построить линейную модель , определив ее параметры методом наименьших квадратов.

Построение модели.

Вначале построим график 2 зависимости y_t от t:

y_t

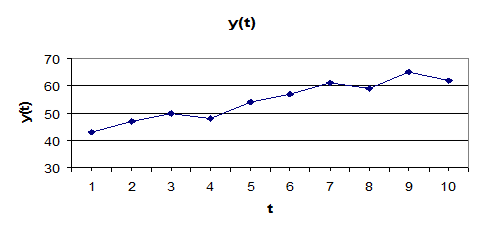
график 2. Исходный временной ряд.

Для выбора полиномиальной кривой методом Тинтнера, как было указано выше в п.2.4.1.1, необходимо сделать предположение, что исходный временной ряд состоит только из тренда и случайной компоненты. Проверка этого предположения будет описана ниже при расчете адекватности модели.

Следуя схеме вычислений по методу Тинтнера, вычислим приросты до 4-го порядка по формуле (39). Полученные значения приведены в таблице 2.

Таблица 2

Значения временного ряда и его приросты.

t	y _t
1	43
2	47	4
3	50	3	-1
4	48	-2	-5	-4
5	54	6	8	13	17
6	57	3	-3	-11	-24
7	61	4	1	4	15
8	59	-2	-6	-7	-11
9	65	6	8	14	21
10	62	-3	-9	-17	-31

Затем находим дисперсии исходного ряда (k=0) по формуле (40), и для разностных рядов (k=1, 2, 3, 4) по формуле (41). После этого вычисляем отклонение каждой последующей дисперсии от предыдущей по формуле (42). Значения этих величин приведены в таблице 3.

Таблица 3

Значения дисперсий и отклонений для исходного ряда и приростов.

k
0	54, 0444
1	7, 72222	46, 3222
2	5, 85417	1, 86806
3	6, 11429	0, 26012
4	6, 22143	0, 10714

Как можно видеть, разности дисперсий уменьшаются с увеличением k и при k=3 достигают приемлемых величин, следовательно, ряд можно аппроксимировать функцией степени k-1=2.

Однако следует исследовать данный временной ряд также методом характеристик прироста, т.к. этот метод, являясь более универсальным, может наложить более строгое условие на степень полиномиальной кривой.

Вначале требуется произвести сглаживание исходного временного ряда простой скользящей средней. В литературе [1], рекомендуется использовать интервал сглаживания m=3. Значения сглаженного временного ряда рассчитываются по формулам (43) и (44). Далее вычисляются первые и вторые средние приросты по формулам (45), (46). Соответствующие значения временного ряда и приростов приведены в таблице 4.

Таблица 4

Значения исходного и сглаженного рядов, а также приросты для сглаженного ряда.

t	y_t	y_t (cглаженная m=3)
1	43	43, 16666667
2	47	46, 66666667	3, 5
3	50	48, 33333333	1, 6667	-1, 83
4	48	50, 66666667	2, 3333	0, 667
5	54	53	2, 3333	0
6	57	57, 33333333	4, 3333	2
7	61	59	1, 6667	-2, 67
8	59	61, 66666667	2, 6667	1
9	65	62	0, 3333	-2, 33
10	62	63, 5	1, 5	1, 167

На графике 3 сопоставлены исходный и сглаженный временные ряды:

график 3. Совмещенный график исходного и сглаженного временных рядов.

Первый и второй приросты не имеют тенденции к изменению и колеблются около средних значений 2, 259 и -0, 25 соответственно. Следовательно, согласно таблице 1, можно использовать полином первого порядка, коэффициенты которого находятся по методу наименьших квадратов.

Метод наименьших квадратов описан в п. 2.4.1.2. Подставляя значения из таблицы 2 в систему уравнений (47) получаем:

откуда находим a₀и a₁:

a₀=34, 8

a₁=3, 6

Таким образом,

В таблице 5 приведены исходные и расчетные значения временного ряда:

Таблица 5

Расчетные и реальные значения временного ряда.

t	_{(расчетн)}	y _t
1	38, 4	43
2	42	47
3	45, 6	50
4	49, 2	48
5	52, 8	54
6	56, 4	57
7	60	61
8	63, 6	59
9	67, 2	65
10	70, 8	62

Ниже на графике 4 изображены расчетные и реальные значения временных рядов:

график 4.Расчетные и реальные значения временного ряда

Заключение.

В теоретической части данной работы были рассмотрены некоторые методы экономического прогнозирования; основное внимание было уделено трендовым моделям на основе кривых роста, а также предварительному анализу и обработке временных рядов.

В практической части по значениям исходного временного ряда была построена трендовая модель на основе полинома первого порядка, а также определены ее адекватность и точность. В результате:

1. Трендовая модель имеет вид: ;

2. На основании анализа случайной компоненты полученная модель признана адекватной.

3. Средняя ошибка аппроксимации попадает в 10%-ный интервал (6, 29%), и таким образом точность модели является удовлетворительной.

4. Необходимы дополнительные исследования с большим объемом статистических данных, т.к. только в этом случае возможно неоднократное применение ретроспективного прогноза, а, следовательно, более точное определение ошибок прогноза и его верификация.