ДПФ в вещественной и комплексной формах.
В предшествующих разделах использованы вещественные коэффициенты  ,
,  ,
,  ,
,  . Для математических преобразований удобнее вместо sin, cos использовать комплексную экспонент
. Для математических преобразований удобнее вместо sin, cos использовать комплексную экспонент  и комплексную форму ДПФ:
и комплексную форму ДПФ:
 , ,
| (2.30)
|
 , ,
| (2.31)
|
Последние формулы получаются из (2.16) - (2.20). Имеем:

Вводя комплексные амплитуды для  и
и  соотношениями
соотношениями
 ,
,  , получим
, получим
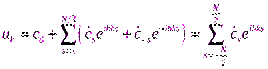 , ,
| (2.32)
|
Гармоники 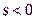 в теоретической радиотехнике соответствуют отрицательным частотам. Напомним, что отрицательная частота позволяет записать вещественный гармонический сигнал в виде двух комплексных экспонент
в теоретической радиотехнике соответствуют отрицательным частотам. Напомним, что отрицательная частота позволяет записать вещественный гармонический сигнал в виде двух комплексных экспонент
 .
.
Используя периодичность спектра 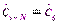 , можно в (2.32) сменить пределы суммирования и получить (2.31). Выражение (2.30) следует из (2.17) – (2.20), т.к.
, можно в (2.32) сменить пределы суммирования и получить (2.31). Выражение (2.30) следует из (2.17) – (2.20), т.к.  .
.
Из (2.31) и (2.32) следует, что для ДПФ в комплексной форме достаточно одной программы, т.к. прямое и обратное ДПФ различаются лишь знаком в экспоненте и множителем  , а не видом формул.
, а не видом формул.
Количество операций в ДПФ.
Оценим количество операций по (2.31). Операцией будем считать умножение на комплексную экспоненту, т.е.  . Операции здесь очень сложные, т.к.
. Операции здесь очень сложные, т.к.  вычисляется через
вычисляется через  ,
,  , а
, а 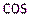 ,
,  через полиномы.
через полиномы.
Имеем 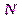 слагаемых для вычисления одной гармоники по (2.31) и поэтому для вычисления одной гармоники нужно
слагаемых для вычисления одной гармоники по (2.31) и поэтому для вычисления одной гармоники нужно  операций. Так как всего вычисляется
операций. Так как всего вычисляется  гармоник
гармоник 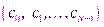 , то прямое ДПФ требует примерно
, то прямое ДПФ требует примерно 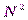 операций, т.е. сложность алгоритма ДПФ
операций, т.е. сложность алгоритма ДПФ  . Это означает, что при увеличении
. Это означает, что при увеличении  в 10 раз, количество операций увеличится в 100 раз.
в 10 раз, количество операций увеличится в 100 раз.
БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (БПФ)
Понятие о БПФ
БПФ – это группа алгоритмов для программной реализации ДПФ, сокращающих количество операций примерно в  раз, т.е.
раз, т.е.  операций вместо
операций вместо  . Другими словами, БПФ - это ДПФ, выполняемое очень быстро. Первый алгоритм БПФ предложен в 1965г, а сейчас их много и они очень сложные. Мы рассмотрим один из них, наиболее простой для понимания. Этот алгоритм, иногда называемый алгоритмом “бабочки”, основан на расщеплении исходного массива отсчетов сигнала. Появление БПФ сделало переворот в цифровой обработке, т.к. позволило легко переходить к преобразованиям спектров в случае больших значений
. Другими словами, БПФ - это ДПФ, выполняемое очень быстро. Первый алгоритм БПФ предложен в 1965г, а сейчас их много и они очень сложные. Мы рассмотрим один из них, наиболее простой для понимания. Этот алгоритм, иногда называемый алгоритмом “бабочки”, основан на расщеплении исходного массива отсчетов сигнала. Появление БПФ сделало переворот в цифровой обработке, т.к. позволило легко переходить к преобразованиям спектров в случае больших значений  .
.
Основу БПФ составляют 4 идеи:
1. Спектр ДПФ – периодический,  .
.
2. Спектр ДПФ легко вычисляется в случае  , когда имеется только одна гармоника и по (14.7)
, когда имеется только одна гармоника и по (14.7) 
3. Выбирается  , где
, где  – целая степень, т.е. количество отсчетов не может быть произвольным целым числом. Например, при
– целая степень, т.е. количество отсчетов не может быть произвольным целым числом. Например, при  имеем
имеем 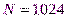 .
.
4. Спектр исходной последовательности несложно найти по спектрам расщепленных последовательностей. При каждом расщеплении от одного массива из  отсчетов переходят к двум массивам из
отсчетов переходят к двум массивам из  отсчетов каждый.
отсчетов каждый.
Вычисление спектра объединенной последовательности по спектрам расщепленных.
Пусть на периоде T имеем два сигнала  и
и 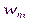 ,
, 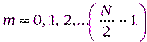 , каждый из которых содержит N/2 точек и имеет безразмерный шаг дискретизации
, каждый из которых содержит N/2 точек и имеет безразмерный шаг дискретизации  . Из этих двух сигналов, объединяя их в виде “гребенки”, получаем объединенную последовательность
. Из этих двух сигналов, объединяя их в виде “гребенки”, получаем объединенную последовательность 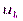 ,
,  , состоящую из
, состоящую из  отсчетов. При таком объединении для четных
отсчетов. При таком объединении для четных  при
при  имеем
имеем  , для нечетных
, для нечетных  при
при  имеем
имеем 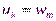 . Например,
. Например,  ,
, 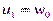 ,
,  ,
,  и т.д. Для объединенного сигнала получается шаг
и т.д. Для объединенного сигнала получается шаг  .
.
Рассматриваемые сигналы даны на рисунке 2.6

|
| Рис. 2.6 Две расщепленных и объединенная последовательности отсчетов.
|
Запишем спектры этих трех сигналов в комплексной форме (14.7), причем для спектров будем использовать заглавные буквы, соответственно строчные - для сигналов.
ДПФ для исходного сигнала (15.3) требует  опреаций в строке (
опреаций в строке (  ) (операция – это вычисление константы, умноженное на
) (операция – это вычисление константы, умноженное на 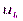 , прибавление к предыдущему), всего
, прибавление к предыдущему), всего  , т.е.
, т.е.  строк, операций
строк, операций  .
.
Здесь суммы по  вычисляются по
вычисляются по  точкам и по этому появляются множители 2 перед суммой и в показателе степени. Количество гармоник в (2.33 – 2.34) равно
точкам и по этому появляются множители 2 перед суммой и в показателе степени. Количество гармоник в (2.33 – 2.34) равно  , а в (2.35) оно равно
, а в (2.35) оно равно  . Покажем, как спектр
. Покажем, как спектр  можно вычислить по спектрам
можно вычислить по спектрам  и
и  :
:
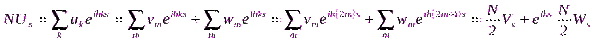 , ,
| (2.36)
|
т.е.  ,
,  .
.
При выводе вместо отсчетов с четными номерами  подставлены значения
подставлены значения  , а вместо отсчетов
, а вместо отсчетов  c нечетными номерами – значения
c нечетными номерами – значения  . Формулу (2.36) можно применять для
. Формулу (2.36) можно применять для 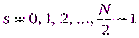 , т.к. спектры
, т.к. спектры  и
и 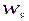 содержат
содержат  гармоник. Но учитывая их периодичность:
гармоник. Но учитывая их периодичность:  ,
,  а также равенство
а также равенство 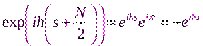 , получаем для гармоник с номерами
, получаем для гармоник с номерами 
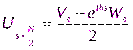
| (2.37)
|
Формулы (2.36-2.37) составляют суть алгоритма “бабочка”, т.к. для его иллюстрации используют рисунок, похожий на бабочку.

|
| Рис.2.7 Иллюстрация к алгоритму “бабочка”.
|
Алгоритм БПФ
Дан массив  из
из  отсчетов сигнала, причем
отсчетов сигнала, причем  .
.
1. Расщепляем его многократно на четные и нечетные последовательности до получения  последовательностей из одного отсчета в каждой, см. рис 13.3.
последовательностей из одного отсчета в каждой, см. рис 13.3.

|
| Рис.2.8 Расщепление последовательностей.
|
На рис. 2.8 значение  дает количество отсчетов в каждой из расщепленных последовательностей. Всего уровней расщепления
дает количество отсчетов в каждой из расщепленных последовательностей. Всего уровней расщепления  , т.е. расщепляем
, т.е. расщепляем  раз. Будем считать, что
раз. Будем считать, что 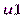 – это новый массив
– это новый массив  точек. В нем порядок следования точек отличен от исходного, т.е.
точек. В нем порядок следования точек отличен от исходного, т.е.  , где
, где  , а индекс
, а индекс  вычисляется по
вычисляется по 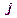 .
.
Оказывается, что преобразование  дает обратный битовый порядок, например,
дает обратный битовый порядок, например,  .
.
Для 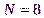 получаем следующее преобразования индексов:
получаем следующее преобразования индексов:


Столь простое преобразование можно не учитывать при оценках времени работы алгоритма.
2. Так как при 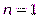 , т.е. при одном отсчете на периоде, спектр равен самому отсчету, то на последнем уровне расщепления (
, т.е. при одном отсчете на периоде, спектр равен самому отсчету, то на последнем уровне расщепления ( 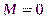 ) спектры всех
) спектры всех  последовательностей известны. Всего имеем
последовательностей известны. Всего имеем  спектров, каждый из которых состоит только из нулевой гармоники (
спектров, каждый из которых состоит только из нулевой гармоники (  ), т.е. среднее значение.
), т.е. среднее значение.
3. Объединение последовательностей, т.е. обратный ход.
При каждом объединении используются формулы для вычисления спектра (13.4-13.5). Вычисления завершаются после получения спектра  из
из  гармоник для исходной последовательности уровня
гармоник для исходной последовательности уровня  .
.
Популярное:

