Корреляционное отношение и индекс корреляции

⇐ ПредыдущаяСтр 3 из 6Следующая ⇒

Введенный выше коэффициент корреляции, как уже отмечено, является полноценным показателем тесноты связи лишь в случае линейной зависимости между переменными. Однако часто возникает необходимость в достоверном показателе интенсивности связи при любой форме зависимости.

Для получения такого показателя вспомним правило сложения дисперсий:

(44, 45)

— средняя групповых дисперсий , или остаточная диспепсия —

(46, 47, 48) межгрупповая дисперсия

Остаточной дисперсией измеряют ту часть колеблемости Y, которая возникает из-за изменчивости неучтенных факторов, не зависящих от X. Межгрупповая дисперсия выражает ту часть вариации У, которая обусловлена изменчивостью X. Величина

(49)

получила название эмпирического корреляционного отношения У по X. Чем теснее связь, тем большее влияние на вариацию переменной доказывает изменчивость X.по сравнению с неучтенными факторами, тем выше n_ух. Величина n_ух., называемая эмпирическим коэффициентом детерминации, показывает, какая часть общей вариации У обусловлена вариацией X. Аналогично вводится эмпирическое корреляционное отношение X по У:

(50)

Отметим основные свойства корреляционных отношений (при достаточно большом объеме выборки п):

1.Корреляционное отношение есть неотрицательная величина, не превосходящая 1: 0< η < 1.

2. Если η = 0, то корреляционная связь отсутствует. Если η = 1, то между переменными существует функциональная зависимость.

3. η _ух≠ η _ху, т.е. в отличие от коэффициента корреляции r (для которого r _ху= r _ух = r ) при вычислении корреляционного отношения существенно, какую переменную считать независимой, а какую — зависимой.

Эти свойства справедливы как для эмпирических корреляционных отношений n, так и для теоретических — R.

Эмпирическое корреляционное отношение η _ух является показателем рассеяния точек корреляционного поля относительно эмпирической линии регрессии, выражаемой ломаной, соединяющей значения . Однако в связи с тем, что закономерное изменение нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов, η _ухпреувеличивает тесноту связи. Поэтому наряду с η _ух. рассматривается показатель тесноты связи R_ух, характеризующий рассеяние точек корреляционного поля относительно линии регрессии у_х (12.3). Показатель R_ух получил название теоретического корреляционного отношения или индекса корреляции Y по X.

(51)

где дисперси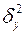и и определяются по формулам (45) —(46), в которых групповые средние , заменены условными средними 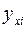, вычисленными по уравнению регрессии (16). Подобно R_ух вводится и индекс корреляции X по Y

(52)

Достоинством рассмотренных показателей η и R является то, что они могут быть вычислены при любой форме связи между переменными. Хотя η и завышает тесноту связи по сравнению с R, но для его вычисления не нужно знать уравнение регрессии. Корреляционные отношения η и R связаны с коэффициентом корреляции r следующим образом:

(53)

Можно показать, что в случае линейной модели (3), т.е. зависимости, y_x- =b_yx(x- ) индекс корреляции R_ух равен коэффициенту корреляции r (по абсолютной ветчине): R_yx = | r |

. (54)

Коэффициент детерминации R², равный квадрату индекса корреляции (для парной линейной модели — r ²), показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной. Чем ближе R² к 1, тем теснее наблюдения примыкают к линии регрессии, тем лучше регрессия описывает зависимость переменных.

Расхождение между η ² и R² (или r ²) может быть использовано для проверки линейности корреляционной зависимости.

Проверка значимости корреляционного отношения η основана на том, что статистика

(55)

(где m — число интервалов по группировочному признаку) имеет F-распределение Фишера—Снедекора с k₁=m — 1 и k₂=n — m степенями свободы. Поэтому η значимо отличается от нуля, если F > F_α,,_k_1,_k₂, где F_α,,_k_1,_k₂— табличное значение F-критерия на уровне значимости α при числе степеней свободы k₁и k₂.

Индекс корреляции R двух переменных значим, если значение статистики

(56)

больше табличного F_α,,_k_1,_k₂, где к₁ = 1 и к.₂ = п — 2.

2. СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ.

АНАЛОГОВОЕ И ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.

2.1. Задача спектрального анализа и цифровая обработка сигналов.

Непрерывную или дискретную функцию одного переменного можно представить рядов Фурье по тригонометрическим функциям , или интегралом Фурье от этих функций. Задача спектрального анализа состоит в определении спектра функции – кооффициентов ряда Фурье и спектральной плотности в интеграле Фурье в зависимости от частоты или круговой частоты . Спектральный анализ сигналов имеет очень важное значение в радиоэлектронике, поэтому функцию обычно рассматривают как сигнал, зависящей от времени .
Цифровая обработка состоит из двух больших областей: спектрального анализа и цифровых фильтров. Обе области рассматривают цифровые сигналы, называемые также дискретными, которые представляются в виде дискретных функций времени с постоянным шагом дискретизации , т.е. время , где – номер отсчета. Цифровой сигнал получается при дискретизации аналогового сигнала , представляемого непрерывной функцией времени.
Алгоритмы цифровой обработки позволяют выполнять различные преобразования дискретных функций, причем можно преобразовывать как сами функции, так и их спектры.
Рассмотрим периодические и непериодические сигналы. В таблице 2.1 приводятся основные характеристики сигналов и их спектров, причем используются следующие обозначения:
Д=1 означает дискретный, Д=0 – аналоговый, П=1 означает периодический, П=0 – непериодический.

Таблица2.1.

Аналоговые и дискретные сигналы и их спектры

Дискретный непериодический сигнал (Д=1, П=0) при цифровой обработке обычно рассматривают как периодический (Д=1, П=1) с большими и физически разумными значениями периода .
Период определяет разрешение в спектре, т.е. разность частот соседних составляющих равна . Очевидно, что при получаем , т.е. сплошной спектр (Д=0).
Количество составляющих в спектре дискретного сигнала определяется количеством отсчетов на периоде .

2.2. Аналоговое преобразование Фурье (АПФ).

АПФ – это преобразование Фурье для аналогового сигнала, представляемого непрырывной функцией .
Переодическую функцию , имеющую период , можно представить рядом Фурье.

(2.1)

где - основная круговая частота сигнала,

- круговая частота -й гармоники сигнала,

(2.2)

- среднее значение (постоянная состовляющая сигнала) сигнала,

(2.3)

- косинусные коэффициенты сигнала,

(2.4)

- синусные коэффициенты сигнала.

Ряд (11.1) можно переписать в виде

(2.5)

Здесь – амплитуда гармоники с номером , – фаза той же гармоники. Значения и определяются по коэффициентам , с помощью формул

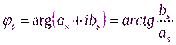
(2.6)

Комплексное число , его модуль и аргумент показаны на рис.2.1.

Рис. 2.1. Определение амплитуды

и фазы

гармоники по коэффициентам

Отметим, что величину называют комплексной амплитудой гармоники.
Для непериодических функций , когда , ряд Фурье (11.1) или (11.2) и выражения для его коэффициентов переходят в интегралы Фурье.

(2.7)

- обратное преобразование Фурье,

(2.8)

- прямое преобразование Фурье.

2.3. Дискретное преобразование Фурье (ДПФ).

ДПФ позволяет вычислять спектр дискретного сигнала, в том числе полученного из аналогового сигнала выборкой его значений , , . Оно основано на следующих положениях.
1. Сигнал является периодическим или периодически продолженным, - период.
2. Сигнал является дискретным и имеет постоянный шаг дискретизации .
3. Отсчеты сигнала на периоде представляются массивом , где – номера отсчетов, .
4. Количество отсчетов на периоде равно .
5. Условие периодичности сигнала имеет вид , т.е. .
6. Формулы ДПФ записываются в безразмерных целых переменных , , где – номера отсчетов сигнала, – номера спектральных составляющих.
7. Номера – это номера гармоник. Для вещественного сигнала (комплексный будет рассмотрен позже) значения для четного , т.е. гармоник вдвое меньше, чем отсчетов сигнала. Нечетные значения возможны, но мы их рассматривать не будем. Значение показывает количество полных колебаний на периоде. Например, на рис.11.2 показан гармонический сигнал для .
8. Для каждой гармоники определяются ее амплитуда и фаза. В вычислениях амплитуд и фаз используются синусных составляющих и косинусных составляющих, т.к. две синусные составляющие и 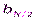являются нулевыми и не учитываются в формулах.

Рис. 2.2. Гармонический сигнал для

Безразмерные переменные

В ДПФ рассматриваются следующие физические переменные, характеризующие сигнал: время , период , частота -ой гармоники , шаг дискретизации , и для каждой переменной используется ее безразмерный аналог, см. таблицу 11.2.

Таблица 2.2

	размерные	безразмерные
Период
Время
Шаг дискретизации		1 или
Частота

– количество отсчетов на периоде, – номера отсчетов, – номера гармоник.
Связь размерных и безразмерных переменных дают простые формулы

(2.9)

где – частота первой гармоники, называемая также основной, - безразмерный шаг дискретизации. Безразмерные переменные позволяют использовать универсальные стандартные подпрограммы ДПФ для любых сигналов, т.к. размерные значения периода и частот в основных формулах не используются. Для спектрального анализа важны номера гармоник, а не размерные значения частот.

Используя (11.1), нетрудно показать, что гармоническое колебание или может быть записано в виде или , т.к. .

⇐ Предыдущая 1 234 5 6 Следующая ⇒