Общая схема принятия решения.

Виды и примеры экономических задач оптимизации и управления

В математической экономике важнейшую роль играют модели принятия решения. Наиболее частое применение находят те из них, которые сводят исходные задачи оптимального планирования производства, рационального распределения ограниченных ресурсов и эффективной деятельности экономических субъектов к экстремальным задачам, к задачам оптимального управления и к игровым задачам. Рассмотрим общую структуру таких моделей.

Любая задача принятия решения характеризуется наличием лица или лиц, преследующих определенные цели и имеющих для этого определенные возможности. Поэтому для выявления основных элементов модели принятия решения требуется ответить на следующие вопросы:

· кто принимает решение?

· каковы цели принятия решения?

· в чем состоит принятие решения?

· каково множество возможных вариантов достижения цели?

· при каких условиях происходит принятие решения?

Для построения общей задачи принятия решения введем общие обозначения.

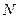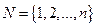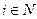Буквой обозначим множество всех сторон, принимающих решение. Пусть , т.е. имеется всего участников, идентифицируемых только номерами. Каждый элемент называется лицом, принимающим решение (ЛПР) (например, отдельная личность, фирма, плановый орган большого концерна, правительства и др.).

Предположим, что множество всех допустимых решений (альтернатив, стратегий) каждого ЛПР предварительно изучено и описано математически (например, в виде системы неравенств). Обозначим их через 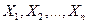. После этого процесс принятия решения всеми ЛПР сводится к следующему: каждое ЛПР выбирает конкретный элемент из своего допустимого множества решений 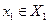, ,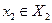..., . 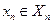В результате получается набор 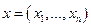выбранных решений, который называется ситуацией.

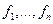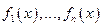Для оценки ситуации с точки зрения преследуемых целей ЛПР строятся функции (называемыми целевыми функциями или критериями качества), ставящие в соответствие каждой ситуации числовые оценки (например, доходы фирм в ситуации , или их затраты и т. д.). Тогда цель 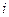-го ЛПР формализуется следующим образом: выбрать такое свое решение 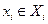, чтобы в ситуации 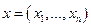число 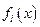было как можно большим (или меньшим). Однако достижение этой цели от 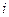-го ЛПР зависит лишь частично в силу наличия других сторон, влияющих на общую ситуацию с целью достижения своих собственных целей. Этот факт пересечения интересов (конфликтность) отражается в том, что функция 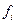кроме 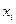зависит и от остальных переменных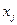 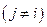. Поэтому в моделях принятия решения со многими участниками их цели формализуются иначе, чем максимизация или минимизация значений функции .

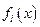Допустим, что удалось математически описать все те условия, при которых происходит принятие решения (описание связей между управляемыми и неуправляемыми переменными, описание влияния случайных факторов, учет динамических характеристик и т. д.). Совокупность всех этих условий для простоты обозначим символом .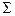

Таким образом, общая схема задачи принятия решения имеет вид:

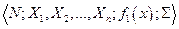(1.6.1)

Конкретизируя элементы модели (1.6.1.), уточняя их характеристики и свойства, можно получить тот или иной конкретный класс моделей принятия решения. Так если в (1.6.1.) 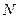состоит только из одного элемента 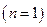, а все условия и предпосылки исходной реальной задачи можно описать в виде множества допустимых решений этого единственного ЛПР, то из (1.6.1.) получаем структуру оптимизационной (экстремальной) задачи: 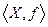, В этой схеме ЛПР может рассматриваться как планирующий орган. С помощью данной схемы можно написать экстремальные задачи двух видов:

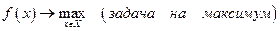
(1.6.2)

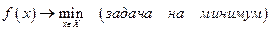
Если в экстремальной задаче явно учитывается фактор времени, то она называется задачей оптимального управления. Если 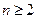, то (1.6.1.) является общей схемой задачи принятия решения в условиях конфликта, т. е. в тех ситуациях, когда имеет место пересечение интересов двух или более сторон.

Часто у ЛПР имеется не одна, а несколько целей. В этом случае из (1.6.1.) получаем схему 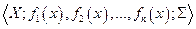, где все функции 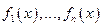определены на одном и том же множестве 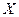. Такие задачи называются задачами многокритериальной оптимизации.

Имеются классы задач принятия решения, получившие свои названия исходя из их назначения: системы массового обслуживания, задачи управления запасами, задачи сетевого и календарного планирования, теория надежности и др.

Если элементы модели (1.6.1.) не зависят явно от времени, т. е. процесс принятия решения сводится к мгновенному выбора точки из заданного множества, то задача называется статической. В противном случае, т. е. когда принятие решения представляет собой многоэтапный дискретный или непрерывный во времени процесс, задача называется динамической. Если элементы модели (1.6.1.) не содержат случайных величин и вероятностных явлений, то задача называется детерминированной, в противном случае - стохастической. Приведем «классические» задачи принятия решения.

Задача оптимального раскроя материала. Фирма изготовляет изделие, состоящее из 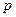деталей. Причем в одно изделие эти детали входят в количествах 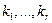. С этой целью производится раскрой 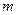партий материала. В 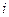-ой партии имеется 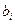единиц материала. Каждую единицу материала можно раскроить на детали способами. При раскрое единицы 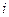-ой партии -м способом получается 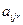деталей 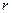-го вида.
Требуется составить такой план раскроя материала, чтобы из них получить максимальное число изделий.

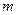Транспортная задача. Имеется поставщиков и потребителей одного и того же продукта. Известны выпуск продукции у каждого поставщика и потребности в ней каждого потребителя, затраты на перевозки продукции от поставщика к потребителю.
Требуется построить план транспортных перевозок с минимальными транспортными расходами с учетом предложения поставщиков и спроса потребителей.

Задача о назначениях на работу. Имеется работ и исполнителей. Стоимость выполнения работы 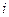исполнителем равна 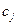. Нужно распределить исполнителей на работы так, чтобы минимизировать затраты на оплату труда.

3адача о смесях (о рационе). Из 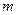видов исходных материалов каждый из которых состоит из компонент, составить смесь, в которой содержание компонент должно быть не меньше 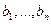.Известны цены единиц материалов 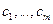и удельный вес -го компонента в единице 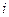-го материала. Требуется составить смесь, в которой затраты будут минимальными.

Задача о рюкзаке. Имеется предметов. Вес предмета 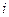равен 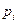, ценность –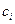 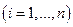. Требуется при заданной ценности груза выбрать совокупность предметов минимального веса.

Задача о коммивояжере. Имеется городов и заданы расстояния 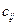между ними 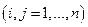. Выезжая из одного (исходного) города, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в исходный город.
Нужно определить в каком порядке следует объезжать города, чтобы суммарное пройденное расстояние было наименьшим.

Задача о станках. На универсальном станке обрабатываются одинаковые партии из деталей. Переход от обработки детали 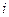к обработке детали требует переналадки станка, которая занимает 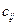времени. Требуется определить последовательность обработки деталей, при которой общее время переналадок станка при обработке партии деталей минимально.

Задача о распределении капиталовложений. Имеется проектов, причем для каждого проекта известны ожидаемый эффект 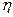от его реализации и необходимая величина капиталовложений 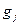. Общий объем капиталовложений не может превышать заданной величины 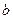. Требуется определить, какие проекты необходимо реализовать, чтобы суммарный эффект был наибольшим.

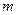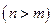Задача о размещении производства. Планируется выпуск видов продукции, которые могли бы производиться на предприятиях . Издержки производства и сбыта единицы продукции, плановый объем годового производства продукции и плановая стоимость единицы продукции каждого вида известны. Требуется из предприятий выбрать такие 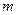, каждое из которых будет производить один вид продукции

⇐ Предыдущая 1 234 Следующая ⇒