
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Случайные величины, числовые характеристики дискретной распределения случайной величины
В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает n счетов. Известно, что a% счетов содержат ошибки. Требуется · составить таблицу распределения вероятностей числа правильных счетов, · найти числовые характеристики этого распределения, · записать функцию распределения вероятностей и построить ее график, · определить вероятность того, что хотя бы 1 счет будет с ошибкой. Пример. Решить задачу для следующих данных: n=4, a=27. Решение. Число правильных счетов есть случайная величина X, которая может принимать значения: 0, 1, 2, 3, 4. Вероятности этих значений определим по формуле Бернулли:
Сделаем проверку. Сумма вероятностей должна быть равна 1. Действительно, Распределение вероятностей случайной величины X содержится в табл.1. Таблица 1 Распределение случайной величины X
Определим числовые характеристики этого распределения. Математическое ожидание дискретной случайной величины X находим по формуле
где
Дисперсию случайной величины X находим по формуле
Так как
То Среднее квадратическое отклонение случайной величины X равно
Найдем функцию распределения вероятностей Если Если Если Если Если
Если 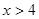 , то , то  . .
График функции Рис.1. График функции распределения
Событие A, состоящее в том, что хотя бы 1 счет будет с ошибкой, является противоположным к событию, что все счета будут правильными, следовательно,
Вероятность того, что хотя бы 1 счет будет с ошибкой, равна Ход работы Задача 1. Плотность распределения случайной величины X имеет вид f (x) = a x 2 e - k x , где k > 0, 0 £ x < ¥. Найти: а) коэффициент a; б) функцию распределения случайной величины X; в) вычислить вероятность попадания случайной величины X на интервал (0; Задача 2. Случайная величина X имеет функцию распределения
Найти: а) плотность распределения f (x), построить графики F (x) и f (x); б) математическое ожидание E(X) и дисперсию D(X); в) вероятность попадания случайной величины X на отрезок [1; 1.5]. Задача 3. Функция распределения непрерывной случайной величины имеет вид F (x) = A + B arctg x, (- ¥ < x < + ¥ ). Найти: а) постоянные A, B; б) плотность распределения f (x), построить графики F (x) и f (x); в) выяснить существует ли E(X)? Задача 4. Плотность распределения случайной величины X имеет вид Найти: а) коэффициент A; б) функцию распределения F (x), построить графики F (x) и f (x); в) математическое ожидание E(X) и дисперсию D(X); г) вероятность попадания случайной величины X в интервал(2; 3); д) вероятность того, что при 4 независимых испытаниях случайная величина X ни разу не попадает на отрезок [2; 3]. Задача 5. График плотности распределения случайной величины X представляет собой полуэллипс с большей полуосью “a” (a - известно).
Задача 6. Функция распределения непрерывной случайной величины X имеет вид Найти: а) коэффициенты а и b; б) математическое ожидание E(X) и дисперсию D(X).
Задача 8. Функция распределения случайной величины X задана графиком
Найти математическое ожидание E(X)и дисперсию D(X).
Задача 10. Случайная величина распределена по закону Коши Найти: а) коэффициент a; б) функцию распределения F (x); в) вероятность попадания случайной величины X на отрезок [-1; 1]. г) выяснить существует ли E(X)? Задача 11. Случайная величина X подчинена показательному закону распределения с параметром l > 0 Найти: а) функцию распределения F (x); б) вероятность того, что случайная величина X примет значение меньшее, чем её математическое ожидание. Задача 12. Случайная величина X подчинена закону Лапласа Найти: а) коэффициент a; б) функцию распределения F (x); в) математическое ожидание E (X) и дисперсию D (X). Задача 13. Функция распределения случайной величины X имеет вид Найти математическое ожидание E (X) и дисперсию D (X). Задача 14. Плотность распределения случайной величины X имеет вид
Найти моменты E(X), D(X), s (X) и вероятность P(0 < X < 2a). Задача 15. Плотность распределения случайной величины X имеет вид
Найти: а) коэффициент a; б) функцию распределения F (x); в) математическое ожидание E (X) и дисперсию D (X); г) вероятность Задача 16. Функция распределения непрерывной случайной величины X имеет вид Найти: а) коэффициенты A, B, C; б) плотность распределения f (x); в) вероятность R (0 < X < 1/2); г) математическое ожидание E (X) и дисперсию D (X); Задача 17. Плотность распределения случайной величины X имеет вид Найти: а) коэффициент A; б) функцию распределения F (x); в) математическое ожидание E (X); г) вероятность R (p / 8 < X < p / 4). Задача 18. Дана функция Найти: а) при каком l функция f (x) является плотностью распре- деления некоторой случайной величины X; б) математическое ожидание E (X) и дисперсию D (X). Задача 19. Дана плотность распределения случайной величины X Найти: а) коэффициент a; б) функцию распределения F (x); в) математическое ожидание E (X) и дисперсию D (X).
Задача 20. Плотность распределения случайной величины X имеет вид Найти: а) коэффициент a; б) функцию распределения F (x); в) математическое ожидание E (X) и дисперсию D (X); г) вероятность P(3 < X < 5).
Задача 21. Дана плотность распределения случайной величины X Найти: а) коэффициент a; б) функцию распределения F (x); в) вероятность R (0 < X < ¥ ).
Задача 22. Плотность распределения случайной величины X имеет вид Найти: а) коэффициент a; б) функцию распределения F (x); в) математическое ожидание E (X) и дисперсию D (X); г) вероятность P (p/2 < X < 3p/2). Задача 23. Плотность распределения случайной величины X имеет вид Найти: а) функцию распределения F (x); б) математическое ожидание E (X) и дисперсию D (X). Задача 24. Плотность распределения случайной величины X имеет вид
Найти: а) математическое ожидание E (X) и дисперсию D (X); б) что вероятнее: в результате испытания окажется, что случай- ная величина X < 1 или что случайная величина X > 1?
Задача 25. Пусть задана функция распределения непрерывной случайной величины X Найти: а) коэффициент a; б) плотность распределения случайной величины f (x); в) математическое ожидание E (X) и дисперсию D (X); г) вероятность R (XÎ (0, 2; 0, 8)). д) построить графики функций f (x) и F (x).
Практическое занятие №9 Основы статистической обработки информации с использованием EXCEL. Определение некоторых числовых характеристик экспериментальных статистических данных.
В табл. № 1 представлены экспериментальные данные, полученные после медицинского обследования 100 студентов. Необходимо оценить числовые характеристики выборки студентов, проанализировать форму распределения частот. Таблица 1 Результаты измерения веса студентов
1. Построить в Excel гистограмму распределения признаков по частотам и полигон частот. Для этого: · найти min и max значения в выборочной совокупности (с помощью статистических функций Excel); · размах варьирования: Rx = xmax - xmin; · число интервалов: k 1+3, 2*log10(n), (где n – количество данных в выборке).Число интервалов всегда округляется до целого (вверх или вниз). · создать массив признаков и посчитать для них частоту.
2. Используя данные выборки студентов, рассчитать: · среднее арифметическое; · медиану; · моду; · дисперсию; · среднее квадратичное отклонение; · эксцесс; · асимметрию распределения (функция СКОС).
Рекомендации к выполнению: Ниже в качестве образца приведен пример выполнения подобной работы. В таблице приведены числовые характеристики, которые рассчитываются с помощью функций Excel, построены полигон и гистограмма частот. Таблица 2 Образец выполнения работы
1. Скопировать массив данных из таблицы 1, расположенной в лабораторной работе. 2. Создать массив интервалов (количество интервалов было вами рассчитано). Первый интервал определяется как сумма минимального элемента выборки и цены деления (C), последний элемент не должен существенно превышать максимального элемента выборки. 3. Выделить ячейки под массив частот (пометить доступными способами). Этих ячеек должно быть столько же, сколько ячеек отведено под массив интервалов. 4. Запустить Мастер Функций 5. После указания всех аргументов функции нажать комбинацию: Ctrl+Shift+Enter. После этого функция ЧАСТОТА заполнит весь выделенный массив. Для построения частот используется функция Excel ЧАСТОТА (массив_данных; массив_интервалов ). Эта функция относится к классу статистических и производит операции над массивами. Массив_данных — ячейки с данными выборки. Массив_интервалов — ячейки, содержащие значения интервалов. Результатом выполнения функции ЧАСТОТА является массив, содержащий частоты вариантов, попадающие в указанные интервалы. На основе этого результирующего массива (в примере — “Частоты”) и строятся гистограммы и полигоны.
Полигон и гистограмма частот строятся по значениям частоты.
1. При каком значении эксцесса полигон частот наиболее заострен? Популярное:
|
Последнее изменение этой страницы: 2016-03-22; Просмотров: 2145; Нарушение авторского права страницы