ВЕКТОРЫ И МАТРИЦЫ. ОСНОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
В данной главе рассматриваются основные числовые характеристики матриц (операторов) и методы их вычисления. Именно знание основных числовых характеристик оператора позволяет прогнозировать воздействие этого оператора в пространстве и позволяет осознанно решать основную задачу – нахождение решения операторного уравнения вида  .
.
Нормы векторов и матриц
В векторном пространстве  можно определить следующий функционал, обладающий свойствами нормы (так называемая
можно определить следующий функционал, обладающий свойствами нормы (так называемая  - норма):
- норма):
 ,
, 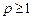 .
.
При различных значениях параметра  получим различные нормы, практически важные из них следующие (при
получим различные нормы, практически важные из них следующие (при  соответственно):
соответственно):
1)  ;
;
2)  ;
;
3) 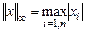 .
.
 Нормы
Нормы  и
и  в векторном пространстве
в векторном пространстве  называются эквивалентными, если существуют такие положительные константы
называются эквивалентными, если существуют такие положительные константы  и
и  , что для любого элемента
, что для любого элемента  выполняется неравенство
выполняется неравенство  .
.
Все  -нормы в пространстве
-нормы в пространстве  эквивалентны. В частности выполнены неравенства:
эквивалентны. В частности выполнены неравенства:
 ;
;  ;
; 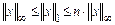 .
.
Из эквивалентности норм  и
и  следует сходимость последовательности в норме
следует сходимость последовательности в норме  при условии ее сходимости в норме
при условии ее сходимости в норме  и наоборот.
и наоборот.
Пример: Вычислить  -нормы вектора
-нормы вектора  .
.
Решение:
1)  ;
;
2)  ;
;
3)  .
.
Так как пространство  матриц изоморфно векторному пространству
матриц изоморфно векторному пространству  , то в нем также определяются
, то в нем также определяются  -нормы, основанные на соответствующих
-нормы, основанные на соответствующих  -нормах векторов по правилу
-нормах векторов по правилу
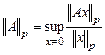 .
.
Т.к.  , то видно, что
, то видно, что  -норма
-норма  матрицы (оператора) есть
матрицы (оператора) есть  -норма наибольшего вектора, полученного действием оператора
-норма наибольшего вектора, полученного действием оператора 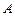 на нормированные (единичной длины в
на нормированные (единичной длины в  -норме) векторы. Построенные так нормы матриц являются операторными или подчиненными соответствующим нормам векторов. Подчиненная норма матрицы (оператора)
-норме) векторы. Построенные так нормы матриц являются операторными или подчиненными соответствующим нормам векторов. Подчиненная норма матрицы (оператора) 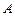 – есть максимальное отклонение от нуля деформированной под действием данного оператора единичной сферы пространства (см.рис. ). Из определения 2.18 следует, что выполнено так называемое условие согласования
– есть максимальное отклонение от нуля деформированной под действием данного оператора единичной сферы пространства (см.рис. ). Из определения 2.18 следует, что выполнено так называемое условие согласования 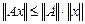 .
.
Таким образом, подчиненная норма – есть наименьшая среди согласованных норм.
Формулы вычисления подчиненных  -норм матриц (при
-норм матриц (при  ) приведены ниже:
) приведены ниже:
1) 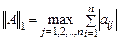 ;
;
2)  ;
;
3) 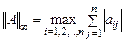 .
.
Наряду с этими нормами рассмотрим евклидову норму матрицы
4)  .
.
Пример: Вычислить  -нормы и евклидову норму матрицы
-нормы и евклидову норму матрицы 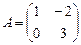 .
.
Решение:
1)  ;
;
2)  ,
,  .
.
Решим характеристическое уравнение для определения собственных значений  . Раскрывая определитель в левой части, получим квадратное уравнение
. Раскрывая определитель в левой части, получим квадратное уравнение  или
или  . Его корни
. Его корни 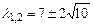 . Наибольшее собственное значение –
. Наибольшее собственное значение –  . Следовательно,
. Следовательно,  .
.
3) 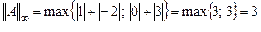 .
.
4) 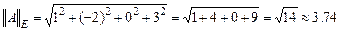 .
.
Введенные нормы эквивалентны, т.к. имеют место оценки:
 ;
; 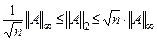 ;
; 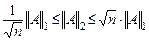 .
.
При практическом применении следует использовать подчиненные нормы векторов и матриц, т.е. если, к примеру, доказана сходимость метода простых итераций в матричной норме 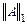 , то и проверку окончания итерационной процедуры необходимо осуществлять в подчиненной норме вектора
, то и проверку окончания итерационной процедуры необходимо осуществлять в подчиненной норме вектора  .
.
 норма матрицы требует вычисления собственных значений
норма матрицы требует вычисления собственных значений  матрицы
матрицы  , что является достаточно сложной задачей для матриц больших размерностей (в этом мы убедимся ниже). Первая оценка, позволяет вместо подчиненной нормы
, что является достаточно сложной задачей для матриц больших размерностей (в этом мы убедимся ниже). Первая оценка, позволяет вместо подчиненной нормы  использовать эквивалентную ей евклидову норму
использовать эквивалентную ей евклидову норму  матрицы, согласованную с нормой
матрицы, согласованную с нормой  вектора.
вектора.
Число обусловленности
Решение операторного уравнения  , как было показано выше на примере СЛАУ второго порядка, может оказаться задачей некорректной в силу неустойчивости получаемого решения
, как было показано выше на примере СЛАУ второго порядка, может оказаться задачей некорректной в силу неустойчивости получаемого решения 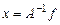 (при условии существования обратного оператора). Решение
(при условии существования обратного оператора). Решение  сильно отклоняется при малых отклонениях правой части
сильно отклоняется при малых отклонениях правой части 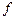 . Это означает, что обратный оператор
. Это означает, что обратный оператор  имеет большую норму (большой коэффициент растяжения), т.е. в матрице
имеет большую норму (большой коэффициент растяжения), т.е. в матрице  возникают большие элементы. Говорят, что такой оператор является плохо обусловленным.
возникают большие элементы. Говорят, что такой оператор является плохо обусловленным.
Пусть  – точное решение уравнения
– точное решение уравнения  , а
, а 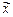 – его приближенное решение. Обозначим через
– его приближенное решение. Обозначим через  – погрешность приближенного решения, а через
– погрешность приближенного решения, а через  – невязку.
– невязку.
Т.к. 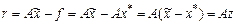 , т.е. погрешность и невязка связаны уравнением
, т.е. погрешность и невязка связаны уравнением  , откуда
, откуда 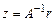 . Т.е. погрешность определяется невязкой. В общем случае ошибочно считать, что малость невязки приводит к малости погрешности в решении. Это не верно в классе плохо обусловленных операторов.
. Т.е. погрешность определяется невязкой. В общем случае ошибочно считать, что малость невязки приводит к малости погрешности в решении. Это не верно в классе плохо обусловленных операторов.
Необходимо определение количественных характеристик оператора, позволяющих судить о взаимосвязи нормы погрешности  и нормы невязки
и нормы невязки  . На практике интерес представляют не абсолютные величины
. На практике интерес представляют не абсолютные величины  и
и  , а их относительные изменения
, а их относительные изменения  и
и  . Важна оценка вида
. Важна оценка вида  . Отыщем коэффициент
. Отыщем коэффициент  , зависящий от оператора
, зависящий от оператора 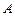 . Т.к.
. Т.к. 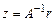 , то
, то 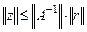 . Т.к.
. Т.к.  , то
, то  . Перемножим эти неравенства. Получим
. Перемножим эти неравенства. Получим  . Деление на
. Деление на 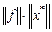 дает
дает  .
.
Коэффициент  называют числом обусловленности линейного обратимого оператора (матрицы).
называют числом обусловленности линейного обратимого оператора (матрицы).
Если число  велико, то оператор
велико, то оператор 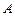 считается плохо обусловленным. Понятие «велико» или «не велико» конечно зависит от конкретной решаемой задачи, от точности, с которой требуется найти решение. Т.к.
считается плохо обусловленным. Понятие «велико» или «не велико» конечно зависит от конкретной решаемой задачи, от точности, с которой требуется найти решение. Т.к. 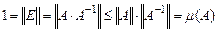 , то число обусловленности – величина не меньшая единицы.
, то число обусловленности – величина не меньшая единицы.
Видно, что число обусловленности зависит от выбора нормы оператора. Оценим его через собственные числа оператора.
Поскольку  и
и  , то
, то  и
и 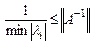 . Тогда
. Тогда
 .
.
Число, вычисляемое как отношение наибольшего по модулю собственного значения оператора к наименьшему по модулю собственному значению, называется числом Тодда. Обозначим его через  . Имеем следующую нижнюю оценку числа обусловленности:
. Имеем следующую нижнюю оценку числа обусловленности:  .
.
Число Тодда есть отношение наибольшей полуоси к наименьшей полуоси эллипсоида рассеяния оператора 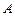 , отношение наибольшего коэффициента растяжения одного собственного подпространства к наименьшему коэффициенту растяжения другого собственного подпространства оператора (см.рис. ).
, отношение наибольшего коэффициента растяжения одного собственного подпространства к наименьшему коэффициенту растяжения другого собственного подпространства оператора (см.рис. ).
В литературе встречаются и иные определения чисел обусловленности [????? ], имеющие вероятностный смысл отношений среднеквадратичных отклонений.
Поскольку большинство методов решения уравнения  основано на последовательном преобразовании
основано на последовательном преобразовании 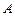 путем умножений слева на элементарные матрицы
путем умножений слева на элементарные матрицы  к некоторому простому виду – диагональному, треугольному и т.д., то следует исследовать как влияют данные умножения на обусловленность.
к некоторому простому виду – диагональному, треугольному и т.д., то следует исследовать как влияют данные умножения на обусловленность.
Справедливы следующие утверждения.
 Если матрица
Если матрица  не вырождена и
не вырождена и  , то умножение матрицы
, то умножение матрицы 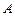 на
на  слева не меняет числа обусловленности матрицы
слева не меняет числа обусловленности матрицы 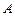 .
.

 тогда и только тогда, когда
тогда и только тогда, когда 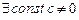 , что
, что 
 .
.
 Число обусловленности инвариантно относительно умножения матрицы на константу, т.е.
Число обусловленности инвариантно относительно умножения матрицы на константу, т.е.  .
.
Замечание: Оператор 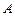 может быть плохо обусловлен, даже если он и не имеет малых собственных значений. С другой стороны, наличие очень малого по модулю собственного значения влечет плохую обусловленность оператора.
может быть плохо обусловлен, даже если он и не имеет малых собственных значений. С другой стороны, наличие очень малого по модулю собственного значения влечет плохую обусловленность оператора.
Замечание: Не верно утверждение, что плохо-обусловленный оператор – есть почти вырожденный оператор (т.е.  ). Условие
). Условие  является необходимым, но не достаточным признаком плохой обусловленности. К примеру, рассмотрим матрицу
является необходимым, но не достаточным признаком плохой обусловленности. К примеру, рассмотрим матрицу  , где
, где  – положительное малое число, а единичная матрица
– положительное малое число, а единичная матрица  – достаточно высокого порядка.
– достаточно высокого порядка. 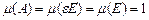 , но определитель при больших
, но определитель при больших 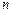 стремиться к нулю, т.к.
стремиться к нулю, т.к.  .
.
Геометрически, плохую обусловленность СЛАУ можно трактовать следующим образом: линейные подпространства, задаваемые уравнениями системы либо сами «почти» параллельны, либо их пересечения образуют «почти» параллельные подпространства меньшей размерности.
Рассмотрим систему  . Она не вырождена –
. Она не вырождена – 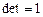 . Ее число обусловленности
. Ее число обусловленности  – велико. Каждое уравнение системы – задает уравнение прямой в плоскости
– велико. Каждое уравнение системы – задает уравнение прямой в плоскости 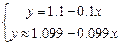 . Видно, что прямые «почти» параллельны. Угловые коэффициенты их близки (
. Видно, что прямые «почти» параллельны. Угловые коэффициенты их близки (  и
и 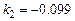 ), но не равны, и, следовательно, прямые пересекаются. Изменение правой части первого уравнения на 0.1 влечет изменение точки пересечения первой прямой с осью
), но не равны, и, следовательно, прямые пересекаются. Изменение правой части первого уравнения на 0.1 влечет изменение точки пересечения первой прямой с осью  на 0.01 и параллельный перенос первой прямой
на 0.01 и параллельный перенос первой прямой  . Точка пересечения этих прямых – новое решение системы – при почти параллельных прямых далеко «убегает» от старого решения (см.рис.).
. Точка пересечения этих прямых – новое решение системы – при почти параллельных прямых далеко «убегает» от старого решения (см.рис.).
Популярное:

