Векторы и матрицы. Основные числовые характеристики.
Норма. Число обусловленности.
Аддитивные и мультипликативные разложения матриц.  -разложение квадратной матрицы,
-разложение квадратной матрицы,  -разложение диагональных матриц.
-разложение диагональных матриц.  -разложение эрмитовых матриц, схема Холецкого. Ортогональные и унитарные матрицы. Разложение матриц с применением ортогональных и унитарных матриц.
-разложение эрмитовых матриц, схема Холецкого. Ортогональные и унитарные матрицы. Разложение матриц с применением ортогональных и унитарных матриц.
Нахождение определителя с использованием мультипликативных разложений матриц.
Проблема собственных значений. Полная и неполная проблема. Прямые и итерационные методы. Метод Данилевского. Метод Леверье. Метод вращений Якоби. Степенной метод. Методы на основе мультипликативных разложений матриц.
Решение систем линейных алгебраических уравнений.
Точные методы. Метод Гаусса. Метод  -разложений. Уточнение решения СЛАУ. Метод прогонки. Метод квадратного корня. Мера обусловленности системы, оценка погрешности приближенного решения системы. Понятие о методе регуляризации решения систем линейных алгебраических уравнений.
-разложений. Уточнение решения СЛАУ. Метод прогонки. Метод квадратного корня. Мера обусловленности системы, оценка погрешности приближенного решения системы. Понятие о методе регуляризации решения систем линейных алгебраических уравнений.
Итерационные методы. Метод простых итераций. Критерий сходимости, достаточные условия сходимости. Оптимизация скорости сходимости итерационных процессов. Метод Якоби. Метод Зейделя. Метод последовательной релаксации.
Обратная матрица. Уточнение элементов обратной матрицы.
ОСНОВНЫЕ ПОНЯТИЯ ВЕКТОРНЫХ, МЕТРИЧЕСКИХ И НОРМИРОВАННЫХ ПРОСТРАНСТВ
 Пусть даны два множества
Пусть даны два множества  и
и  . Говорят, что на множестве
. Говорят, что на множестве  определен оператор, отображающий множество
определен оператор, отображающий множество  в множество
в множество  , если задано правило, по которому каждому элементу
, если задано правило, по которому каждому элементу  однозначно ставится в соответствие определенный элемент
однозначно ставится в соответствие определенный элемент  . Пишут
. Пишут  .
.
 Оператор, действующий из множества
Оператор, действующий из множества  в множество действительных чисел (
в множество действительных чисел ( 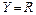 ) называется функционалом.
) называется функционалом.
 Множество
Множество  называется метрическим пространством, если для любой пары
называется метрическим пространством, если для любой пары  его элементов определен неотрицательный функционал
его элементов определен неотрицательный функционал  , называемый расстоянием (метрикой), удовлетворяющий аксиомам:
, называемый расстоянием (метрикой), удовлетворяющий аксиомам:
1)  тогда и только тогда, когда
тогда и только тогда, когда 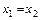 ;
;
2)  для любых
для любых  ;
;
3) 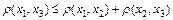 для любых
для любых  (неравенство треугольника).
(неравенство треугольника).
 Последовательность
Последовательность  элементов метрического пространства
элементов метрического пространства  называется сходящейся в метрике
называется сходящейся в метрике  к элементу
к элементу  если
если  .
.
 Последовательность
Последовательность  элементов метрического пространства
элементов метрического пространства  называется фундаментальной, если для любого
называется фундаментальной, если для любого 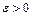 найдется такой номер
найдется такой номер  , что для всех
, что для всех  будет выполняться неравенство
будет выполняться неравенство 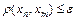 .
.
 Любая сходящаяся последовательность метрического пространства – фундаментальна (обратное не всегда верно).
Любая сходящаяся последовательность метрического пространства – фундаментальна (обратное не всегда верно).
 Метрическое пространство
Метрическое пространство  называется полным, если всякая фундаментальная последовательность его элементов сходится к элементу этого пространства.
называется полным, если всякая фундаментальная последовательность его элементов сходится к элементу этого пространства.
 Множество
Множество  называется линейным (векторным) пространством, если в нем определены операции сложения (+) элементов и умножения (∙ ) элемента на число, не выводящие за пределы
называется линейным (векторным) пространством, если в нем определены операции сложения (+) элементов и умножения (∙ ) элемента на число, не выводящие за пределы  и удовлетворяющие следующим аксиомам:
и удовлетворяющие следующим аксиомам:
1) сложение ассоциативно: 
 ;
;
2) сложение коммутативно: 
 ;
;
3) существует нейтральный по отношению к операции сложения (нулевой) элемент  , такой что
, такой что 
 ;
;
4) 
 ;
;
5)  и
и 
 ;
;
6)  и
и 
 ;
;
7)  и
и 
 ;
;
8) 
 .
.
 Система элементов
Система элементов  линейного пространства
линейного пространства  называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа  одновременно не равные нулю, что
одновременно не равные нулю, что  . Если это равенство выполняется только при
. Если это равенство выполняется только при  , то система называется линейно независимой.
, то система называется линейно независимой.
 Множество
Множество  называется линейным нормированным пространством, если
называется линейным нормированным пространством, если  – линейное пространство, на котором определен вещественный функционал
– линейное пространство, на котором определен вещественный функционал  , т.е. каждому
, т.е. каждому  поставлено в соответствие вещественное число
поставлено в соответствие вещественное число  , называемое нормой и удовлетворяющее аксиомам:
, называемое нормой и удовлетворяющее аксиомам:
1)  , причем
, причем 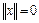 тогда и только тогда, когда
тогда и только тогда, когда  ;
;
2)  ,
,  ;
;
3)  ,
, 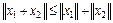 .
.
 Элемент
Элемент  называется нормированным, если
называется нормированным, если  .
.
Линейное нормированное пространство – есть частный случай метрического пространства, в котором норма определена метрикой.
 Полное линейное нормированное пространство называется банаховым.
Полное линейное нормированное пространство называется банаховым.
 Говорят, что в линейном пространстве
Говорят, что в линейном пространстве  определено скалярное произведение, если каждой паре элементов
определено скалярное произведение, если каждой паре элементов  ставится в соответствие вещественное число
ставится в соответствие вещественное число  , обладающее следующими свойствами:
, обладающее следующими свойствами:
1) 
 , причем
, причем 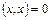 тогда и только тогда, когда
тогда и только тогда, когда  ;
;
2)  ,
,  ;
;
2)  и
и  ,
,  .
.
 Элементы
Элементы  называются ортогональными, если
называются ортогональными, если  . Ортогональность элементов обозначается так:
. Ортогональность элементов обозначается так:  .
.
 Если в линейном пространстве определено скалярное произведение, то в нем можно определить норму
Если в линейном пространстве определено скалярное произведение, то в нем можно определить норму  и расстояние (квадратичную метрику)
и расстояние (квадратичную метрику)  . Метрическое пространство, с метрикой, простроенной на основе скалярного произведения называется предгильбертовым или унитарным.
. Метрическое пространство, с метрикой, простроенной на основе скалярного произведения называется предгильбертовым или унитарным.
 Полное унитарное пространство называется гильбертовым.
Полное унитарное пространство называется гильбертовым.
 Если в унитарном пространстве последовательность
Если в унитарном пространстве последовательность  сходится, т.е
сходится, т.е  , то
, то  .
.
 Если в унитарном пространстве последовательность
Если в унитарном пространстве последовательность  фундаментальна, то последовательность соответствующих норм
фундаментальна, то последовательность соответствующих норм  сходится.
сходится.
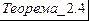 Если в унитарном пространстве последовательность
Если в унитарном пространстве последовательность  фундаментальна, то она ограничена, т.е.
фундаментальна, то она ограничена, т.е.  ,
, 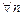
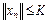 .
.
 Оператор
Оператор  называется линейным, если он определен на линейном пространстве
называется линейным, если он определен на линейном пространстве  и является аддитивным и однородным:
и является аддитивным и однородным:
1)  ,
,  (аддитивность);
(аддитивность);
2) 

 (однородность).
(однородность).
 Множество значений линейного оператора линейно.
Множество значений линейного оператора линейно.
 Если для линейного оператора
Если для линейного оператора  существует обратный оператор
существует обратный оператор  , то
, то  – линейный оператор.
– линейный оператор.
 Пусть
Пусть  – метрическое пространство. Оператор
– метрическое пространство. Оператор  называется сжимающим, если существует такое число
называется сжимающим, если существует такое число  , что для
, что для 
 .
.
 (Банаха о неподвижной точке) (Принцип сжимающих отображений)
(Банаха о неподвижной точке) (Принцип сжимающих отображений)
Пусть  – сжимающий оператор в полном метрическом пространстве
– сжимающий оператор в полном метрическом пространстве  , тогда уравнение
, тогда уравнение  в этом пространстве имеет одно и только одно решение
в этом пространстве имеет одно и только одно решение  (т.е.
(т.е.  ). Элемент
). Элемент 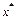 может быть получен как предел последовательности
может быть получен как предел последовательности  с произвольным начальным членом
с произвольным начальным членом 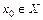 .
.
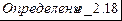 Оператор
Оператор  называется ограниченным в
называется ограниченным в  , если
, если  ,
, 
 . Наименьшее из таких констант
. Наименьшее из таких констант  называется нормой оператора.
называется нормой оператора.
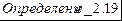 Оператор
Оператор  называется непрерывным в точке
называется непрерывным в точке 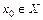 , если для любой последовательности элементов
, если для любой последовательности элементов  для которой
для которой  , последовательность
, последовательность  сходится к
сходится к  , т.е.
, т.е.  или
или  . Если оператор непрерывен во всех точках
. Если оператор непрерывен во всех точках  , то говорят, что он непрерывен в
, то говорят, что он непрерывен в  .
.
 Пусть
Пусть  – линейный оператор в гильбертовом пространстве
– линейный оператор в гильбертовом пространстве  . Если он ограничен в
. Если он ограничен в  , то он так же и непрерывен в
, то он так же и непрерывен в  .
.
КОРРЕКТНОСТЬ. АППРОКСИМАЦИЯ
«… вся наука подчинена идее
аппроксимации …»
Б. Рассел
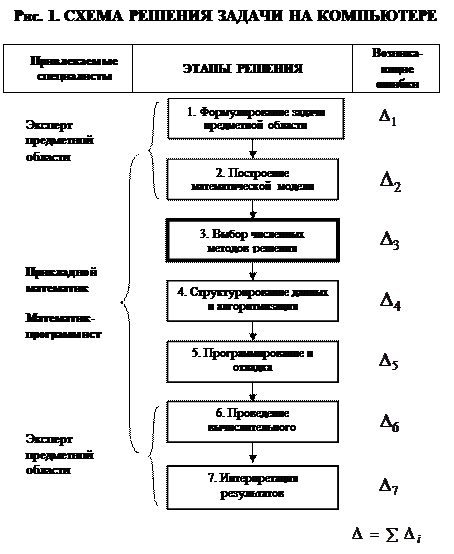
Внимательно посмотрите на схему решения задачи на компьютере (рис.1.). Видно, что начиная с момента формализации задачи, т.е. с этапа построения математической модели и до интерпретации результатов специалистами предметной области, явно необходимо присутствие как математика-прикладника, способного после этапа моделирования построить и численно реализовать алгоритм решения задачи, так и математика-программиста, который обоснованно осуществит выбор вычислительного метода решения и программно его реализует с максимально возможной для данной компьютерной системы эффективностью. Следовательно, и тем и другим необходимо знание основных численных методов решения задач.
Важно так же понимание того, что каждый этап привносит свою ошибку (устранимую и/или неустранимую) в окончательное решение задачи. Выбор численных методов, необходимых для реализации модели должен быть сделан с осознанием привносимой ими ошибки. Грубость выбора численного метода должна быть соизмерима с величинами ошибок (особенно неустранимых) других этапов. Другими словами, нет смысла выбирать «суперточный» метод, когда математическая модель весьма груба. Но с другой стороны, высокая точность примененного численного метода при плохих результатах вычислительного эксперимента поможет обратить внимание на выявление и необходимость уменьшения ошибок на других этапах.
Точность метода связана с затратами ресурсов вычислительной системы. Повышение точности, как правило ведет к повышению времени работы системы и к увеличению требуемого объема памяти. Эффективность метода в свою очередь зависит от мощности множества задач, к которым может данный метод быть применен. Чем шире класс решаемых данным методом задач, следовательно, чем метод универсальнее, тем метод менее эффективен. Найдется такая задача в классе, на которой метод будет давать плохие показатели времени, величины погрешности и т.п. И обратно, сужение класса решаемых задач позволяет модифицировать метод с учетом дополнительных свойств и ограничений, повысив его эффективность. Универсальность метода при этом теряется, метод становится узкоспециальным. «Что-либо приобретая, мы что-то теряем» – эта общая философская сентенция четко работает и в курсе «Численных методов».
Любая исходная задача на языке теории операторов может быть описана следующим образом
 ,
,
где  – некоторые метрические пространства,
– некоторые метрические пространства,  и
и  – подмножества в пространствах
– подмножества в пространствах  и
и  соответственно, определяемые ограничениями задачи на элементы
соответственно, определяемые ограничениями задачи на элементы 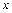 и
и 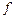 , а
, а  – оператор или закон, по которому каждому элементу
– оператор или закон, по которому каждому элементу 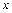 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 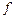 .
.
Если оператор  известен и элемент
известен и элемент 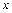 известен, то говорят, что имеет место прямая задача поиска элемента
известен, то говорят, что имеет место прямая задача поиска элемента 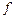 по элементу
по элементу 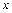 .
.
Например: Пусть  – пространство прямоугольных матриц,
– пространство прямоугольных матриц,  – подмножество квадратных матриц,
– подмножество квадратных матриц,  – есть правило нахождения определителя матрицы, тогда для каждой квадратной матрицы можно найти число
– есть правило нахождения определителя матрицы, тогда для каждой квадратной матрицы можно найти число  . Таким образом, нахождение определителя квадратной матрицы – есть прямая задача.
. Таким образом, нахождение определителя квадратной матрицы – есть прямая задача.
Если же ищется неизвестный элемент  при известных
при известных 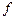 и
и 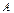 , то имеет место обратная задача. Иногда, когда может быть явно построен оператор обращения
, то имеет место обратная задача. Иногда, когда может быть явно построен оператор обращения  , то решение обратной задачи можно свести к решению прямой задачи вида
, то решение обратной задачи можно свести к решению прямой задачи вида  .
.
 Задача
Задача
 (1)
(1)
называется корректной или корректно поставленной по Адамару, на паре метрических пространств  , если выполняются условия существования, единственности и устойчивости решения:
, если выполняются условия существования, единственности и устойчивости решения:
1) для любого  существует решение
существует решение  ;
;
2) это решение  единственно;
единственно;
3) решение устойчиво, т.е. для любой сходящейся к 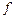 в метрике пространства
в метрике пространства  последовательности элементов
последовательности элементов 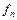 последовательность
последовательность  будет сходится к
будет сходится к  в метрике пространства
в метрике пространства  . Это означает, что обратный оператор
. Это означает, что обратный оператор  непрерывен.
непрерывен.
В противном случае задача называется некорректной или некорректно поставленной.
Корректность задачи напрямую связана с выбором пространств  и метрик в них, а также множеств
и метрик в них, а также множеств  и
и  (с ограничениями на искомые решения). Задача может быть корректна на одной паре пространств и не являться корректной на другой паре. Очевидно, что при расширении пространства
(с ограничениями на искомые решения). Задача может быть корректна на одной паре пространств и не являться корректной на другой паре. Очевидно, что при расширении пространства 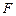 , может оказаться, что не для любого
, может оказаться, что не для любого  решение задачи (1) может существовать. Если оператор
решение задачи (1) может существовать. Если оператор 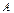 линеен, а пространства
линеен, а пространства  – банаховы, то для корректности задачи необходимо и достаточно существование ограниченного обратного оператора
– банаховы, то для корректности задачи необходимо и достаточно существование ограниченного обратного оператора  из
из 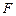 в
в  , причем с областью определения, совпадающей с пространством
, причем с областью определения, совпадающей с пространством 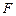 .
.
Приведем классический пример академика А.Н.Тихонова некорректности по Адамару задачи решения систем линейных алгебраических уравнений. Пусть дана СЛАУ вида
 с невырожденной (
с невырожденной (  ) матрицей.
) матрицей.
Ее решение очевидно находится:  . Изменим в системе правую часть первого уравнения на 0.1, получив систему вида
. Изменим в системе правую часть первого уравнения на 0.1, получив систему вида
 .
.
Решение новой системы  в евклидовой метрике пространства
в евклидовой метрике пространства  достаточно далеко (
достаточно далеко (  ) отстоит от первого. Решение оказалось неустойчивым к малым вариациям правой части задачи, в силу плохой обусловленности матрицы системы (мы сможем убедиться в этом в следующей главе).
) отстоит от первого. Решение оказалось неустойчивым к малым вариациям правой части задачи, в силу плохой обусловленности матрицы системы (мы сможем убедиться в этом в следующей главе).
Приведем еще два примера, когда решение задачи не существует (не выполняется условие 1 определения корректности по Адамару) и когда оно существует, но не является единственным (не выполняется условие 2).
Первому случаю соответствует, например, СЛАУ вида
 .
.
Здесь решения нет в соответствии с теоремой Кронекера-Капелли, поскольку ранг матрицы 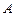 не равен рангу расширенной матрицы.
не равен рангу расширенной матрицы.
Второму случаю соответствует система вида
 .
.
Здесь бесконечное множество решений вида  , где
, где 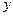 выступает в роли параметра.
выступает в роли параметра.
Ранее считалось, что некорректные задачи не имеют физического смысла, и поэтому их не рассматривали. Однако развитие прикладных наук показывает, что многие важные задачи практики являются по Адамару некорректно поставленными. А.Н. Тихоновым было предложено новое понятие корректности, которое является физически оправданным для многих некорректных по Адамару задач. Рассматривается существенно более узкое, чем все пространство  , множество
, множество  . Пусть образ множества
. Пусть образ множества  при отображении
при отображении 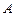 – есть множество
– есть множество  .
.
 Задача (1) называется условно корректной или корректной по Тихонову, если для нее выполнены следующие условия:
Задача (1) называется условно корректной или корректной по Тихонову, если для нее выполнены следующие условия:
1) известно априори, что решение задачи существует и принадлежит некоторому заданному множеству  ;
;
2) решение задачи единственно на множестве  ;
;
3) бесконечно малым вариациям  , не выводящим решение за пределы множества
, не выводящим решение за пределы множества  , соответствуют бесконечно малые вариации решения.
, соответствуют бесконечно малые вариации решения.
Множество  называется множеством корректности задачи.
называется множеством корректности задачи.
Например, задача поиска квадратной матрицы по известному определителю в общем случае, задача не корректная, поскольку ее решение даже в множестве матриц размерности 2х2 не единственно (многим матрицам могут соответствовать одинаковые определители). Но ограничение на поиск решений в множестве матриц размерности 1х1 делает эту задачу корректной.
Заметим, что в условно-корректных задачах нет необходимости доказывать теорему единственности решения задачи (1), т.к. постулируется, что решение на некотором множестве  существует.
существует.
Если оператор 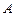 непрерывен, а множество
непрерывен, а множество  компактно, то существует непрерывный обратный оператор, который обеспечивает условие устойчивости 3) определения. Актуальным в этом случае становится доказательство теоремы единственности решения.
компактно, то существует непрерывный обратный оператор, который обеспечивает условие устойчивости 3) определения. Актуальным в этом случае становится доказательство теоремы единственности решения.
Некоторые некорректные по Адамару задачи являются корректными по Тихонову.
В основе компьютерных способов решения большинства задач практики, являющихся, как правило, нелинейными и бесконечномерными, превалируют две идеи: 1) линеаризация (замена нелинейных функций, операторов, множеств линейными) и 2) переход к пространствам конечных размерностей (выбор конечного базиса, переход от интеграла или бесконечного ряда к конечным суммам, замена интервалов на дискретные конечные множества точек (сетки) и т.д.). Переход к конечномерным пространствам необходим по крайней мере, в силу конечности числа хранящих информацию ячеек памяти компьютера и требованием конечности алгоритма вычисления решения задачи.
Задачи при этом сводятся к линейным операторным уравнениям вида  в конечномерных пространствах
в конечномерных пространствах  , где оператором
, где оператором  является матрица. Уравнение
является матрица. Уравнение  – есть не что иное, как система линейных алгебраических уравнений. Именно поэтому задачам линейной алгебры: вычислению числовых характеристик матриц и методам решения систем линейных алгебраических уравнений уделяется повышенное внимание в курсах математики и численных методов высшей школы.
– есть не что иное, как система линейных алгебраических уравнений. Именно поэтому задачам линейной алгебры: вычислению числовых характеристик матриц и методам решения систем линейных алгебраических уравнений уделяется повышенное внимание в курсах математики и численных методов высшей школы.

|
| Рис.2. Аппроксимация задачи.
|
Связь между пространствами  и
и  будем определять оператором
будем определять оператором  , а между пространствами
, а между пространствами 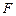 и
и  – оператором
– оператором  . Операторы
. Операторы  и
и  называются операторами сноса. Оператор
называются операторами сноса. Оператор  назовем оператором восполнения (см. рис. 2.). В общем случае оператор
назовем оператором восполнения (см. рис. 2.). В общем случае оператор  не является обратным оператору
не является обратным оператору  (
(  ). Уравнение
). Уравнение  заменяется на уравнение
заменяется на уравнение  . (2)
. (2)
Предположим, что его решение –  – единственно. Так как
– единственно. Так как  и не принадлежит пространству
и не принадлежит пространству  , то, следовательно,
, то, следовательно,  мы не вправе называть приближенным решением исходного уравнения (1). Будем называть его каркасом приближенного решения. Приближенным решением уравнения (1) будем называть элемент
мы не вправе называть приближенным решением исходного уравнения (1). Будем называть его каркасом приближенного решения. Приближенным решением уравнения (1) будем называть элемент 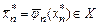 . Отметим, что элемент
. Отметим, что элемент  может и не принадлежать области задания оператора
может и не принадлежать области задания оператора 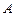 .
.
Если обозначить точное решение уравнения (1) через  , то можно в метрике пространства
, то можно в метрике пространства  измерить расстояние
измерить расстояние  между точным и приближенным решением. Говорят, что имеет место сходимость приближенных решений, если
между точным и приближенным решением. Говорят, что имеет место сходимость приближенных решений, если  . Можно также рассматривать расстояние между каркасом приближенного решения
. Можно также рассматривать расстояние между каркасом приближенного решения  и сносом
и сносом 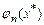 в пространство
в пространство  точного решения – величину
точного решения – величину  . Если
. Если  , то говорят, что имеет место сходимость каркасов приближенных решений.
, то говорят, что имеет место сходимость каркасов приближенных решений.

|
| Рис.3. Погрешность аппроксимации.
|
Говорить о сходимости приближенных решений можно лишь тогда, когда уравнение (2) аппроксимирует уравнение (1).  Уравнение (2) аппроксимирует уравнение (1) (оператор
Уравнение (2) аппроксимирует уравнение (1) (оператор  аппроксимирует оператор
аппроксимирует оператор 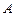 ), если погрешность аппроксимации
), если погрешность аппроксимации  стремиться к нулю при
стремиться к нулю при  .
.
Для лучшего запоминания изучите рисунок 3, на котором погрешность аппроксимации  – есть расстояние между двумя элементами пространства
– есть расстояние между двумя элементами пространства  .
.
Схемы 2 и 3 являются общими схемами аппроксимации исходной задачи. Они имеют место и в случае применения сеточных методов решения задач, когда вместо искомой функции  ищется сеточная функция
ищется сеточная функция  , определяемая на множестве
, определяемая на множестве 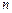 дискретных точек (сетке). Оператор сноса при этом есть оператор проецирования. Оператор восполнения может быть представлен, например, оператором интерполирования.
дискретных точек (сетке). Оператор сноса при этом есть оператор проецирования. Оператор восполнения может быть представлен, например, оператором интерполирования.
Методы решения задачи  делятся на следующие основные классы: 1) методы точные, в которых точное решение задачи определяется за конечное число шагов в предположении отсутствия ошибок округления; 2) методы итерационные, в которых точное решение может быть найдено лишь как результат бесконечной итерационной процедуры, которая представляет собой правило определения последующего приближения на основе нескольких ранее вычисленных приближений; 3) методы вероятностные, в которых задействован аппарат теории вероятности и решение задачи – есть величина, для которой определена лишь вероятность ее попадания в окрестность точного решения.
делятся на следующие основные классы: 1) методы точные, в которых точное решение задачи определяется за конечное число шагов в предположении отсутствия ошибок округления; 2) методы итерационные, в которых точное решение может быть найдено лишь как результат бесконечной итерационной процедуры, которая представляет собой правило определения последующего приближения на основе нескольких ранее вычисленных приближений; 3) методы вероятностные, в которых задействован аппарат теории вероятности и решение задачи – есть величина, для которой определена лишь вероятность ее попадания в окрестность точного решения.
Точные методы, как правило, применяются для задач небольших размерностей (  ), итерационные – для задач размерности
), итерационные – для задач размерности  , вероятностные для задач больших размерностей (
, вероятностные для задач больших размерностей ( 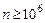 ).
).
В дальнейшем, в данном пособии будем рассматривать линейное операторное уравнение  , в котором будем опускать индекс
, в котором будем опускать индекс 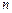 , считая, что элементы
, считая, что элементы  и
и 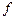 – есть элементы
– есть элементы 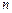 -мерного векторного нормированного пространства
-мерного векторного нормированного пространства  :
:  ,
,  .
.
Линейный оператор 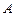 однозначно связан с матрицей. В [1] показано, что матрица
однозначно связан с матрицей. В [1] показано, что матрица 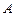 определяет линейный оператор и линейный оператор определяет матрицу. Это соответствие сохраняется при действиях над операторами: матрица суммы операторов равна сумме матриц слагаемых и матрица произведения операторов равна произведению матриц сомножителей.
определяет линейный оператор и линейный оператор определяет матрицу. Это соответствие сохраняется при действиях над операторами: матрица суммы операторов равна сумме матриц слагаемых и матрица произведения операторов равна произведению матриц сомножителей.
Следовательно, под оператором 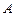 можно понимать квадратную матрицу размерности
можно понимать квадратную матрицу размерности  с элементами
с элементами 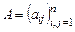 , считая ее элементом нормированного пространства матриц.
, считая ее элементом нормированного пространства матриц.
При изменении базиса пространства по закону 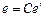 , где
, где  – вектор столбец из координат вектора
– вектор столбец из координат вектора  в новом базисе, матрица оператора
в новом базисе, матрица оператора 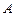 в старом базисе будет связана с матрицей
в старом базисе будет связана с матрицей  этого оператора в новом базисе соотношением
этого оператора в новом базисе соотношением  . Такое преобразование называется преобразованием подобия. При этом преобразовании основные числовые характеристики оператора не изменяются, т.е. инвариантны.
. Такое преобразование называется преобразованием подобия. При этом преобразовании основные числовые характеристики оператора не изменяются, т.е. инвариантны.
 .
.
Популярное:

