RLC-контур. Свободные колебания

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 6.4).

Рис. 6.4.

Когда ключ K находится в положении 1, конденсатор С заряжается до напряжения ε . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер. Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде

(6.9)

,

где – напряжение на конденсаторе, q – заряд конденсатора, – ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t):

(6.10)

.

Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

(6.11)

.

Здесь принято обозначение: . Это уравнение описывает свободные колебания в LC-контуре в отсутствие затухания. Оно в точности совпадает по виду с уравнением свободных колебаний груза на пружине в отсутствие сил трения. Рис. 6.5 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока I(t) и скорости груза υ (t) за один период колебаний.

Рис. 6.5.

Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 6.1.

 

Таблица 6.1

Электрические величины Механические величины Заряд конденсатора q(t) Координата x(t) Ток в цепи Скорость Индуктивность L Масса m Величина, обратная электроемкости Жесткость k Напряжение на конденсаторе Упругая сила kx Энергия электрического поля конденсатора Потенциальная энергия пружины Магнитная энергия катушки Кинетическая энергия Магнитный поток LI Импульс mυ

(6.11)

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

q(t) = q₀cos(ω t + φ ₀).

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний

(6.12)

.

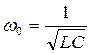Амплитуда q₀ и начальная фаза φ ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 6.4) после переброса ключа K в положение 2, q₀ = Cε , φ ₀ = 0.

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

(6.13)

.

(6.13)

Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 6.6).

Рис.6.6.

Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела:

F_тр = – β v.

Коэффициент β в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид

(6.14)

.

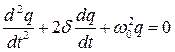Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция

(6.15)

,

которая содержит множитель exp (–δ t), описывающий затухание колебаний. Скорость затухания зависит от электрического сопротивления R контура. Интервал времени , в течение которого амплитуда колебаний уменьшается в e ≈ 2, 7 раза, называется временем затухания.

Добротность Q колебательной системы определяется:

(6.16)

,

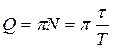где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

(6.17)

Для RLC-контура добротность Q выражается формулой

(6.18)

.

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен. Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω ₀ идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Популярное:

1. Вибрация (механические колебания)
2. Колебания в большевистском ЦК
3. Несвободные: холопы или рабы.
4. Свободные колебания системы с одной степенью свободы.
5. ТЕМА: МАКРОЭКОНОМИЧЕСКИЕ КОЛЕБАНИЯ. ЭКОНОМИЧЕСКИЙ ЦИКЛ
6. Электромагнитные колебания и волны