Электрическое поле. Напряженность поля.

Стр 1 из 5Следующая ⇒

ЭЛЕКТРОДИНАМИКА.

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

И ВОЛНЫ

Методические указания к выполнению

лабораторного практикума по физике

с использованием пакета «Открытая физика 2.5»

Часть 2.1

Уфа 2007

Составитель: А.Г. Саенко, доцент, к.т.н.

УДК 535.3;

Электродинамика. Электромагнитные колебания и волны: Методические указания к выполнению лабораторного практикума по физике с использованием пакета «Открытая физика 2.5». Часть 2.1 / Сост.: А.Г. Саенко.- Уфа: Уфимск. гос. акад. экон. и сервиса, 2007.- 76 с.

В методических указаниях приведена краткая теория изучаемого вопроса, порядок выполнения и правила оформления лабораторных работ по физике разделы «Электродинамика. Электромагнитные колебания и волны» с использованием пакета «Открытая физика 2.5».

Предназначены для студентов дневной и заочной формы обучения инженерных специальностей.

Рис.63, Библиогр.: 5 назв.

Рецензент: С.В. Шапиро, профессор, д.т.н.

А.Г. Саенко, 2007

Уфимская государственная

академия экономики и сервиса, 2007

СОДЕРЖАНИЕ

Лабораторная работа №1. Электрическое поле ……………………………… 6

Лабораторная работа №2. Цепи постоянного тока ………………………... 21

Лабораторная работа №3. Магнитное поле вокруг проводников с токами 32

Лабораторная работа №4. Движение заряда в магнитном поле …………..41

Лабораторная работа №5. Электромагнитная индукция ………………….48

Лабораторная работа №6. Электромагнитные колебания и волны ………58

Данные методические указания направлены на определение порядка выполнения и оформления компьютерных лабораторных работ по программе «Открытая физика 2.5».

Данный пакет предназначен для изучений основных физических законов и явлений с использованием компьютерных моделей студентами очной и заочной форм обучения. Проверка знаний студента проводится во время аудиторных занятий и с помощью контрольных работ, после чего следует тестирование знаний студентов.

Интерфейс программы достаточно удобный и позволяет работать как с теоретическими материалами, так и с моделями одновременно. Кроме этого в пакете присутствует список основных физических констант, формул основных физических законов, приведены биографии великих физиков. Все это позволяет студентам всесторонне подойти к изучению необходимого материала. В пособии учтены особенности учебных планов разных специальностей. Для этого приведены таблицы с указанием количества выполняемых работ для каждого раздела лабораторного практикума.

Практические занятия по данной программе разделяются на:

1) лабораторный практикум;

2) контрольные (домашние) работы.

Лабораторный практикум состоит из 6 лабораторных работ.

Для выполнения домашних контрольных работ каждый студент обеспечивается копией данного пакета.

План проведения занятий

Таблица 1.

Количество занятий по учебному плану	Распределение занятий по разделам	Контрольная работа
	2 – электричество 3 – магнитное поле 1 - тестирование	Все физические модели и задачи
	1 – электромагнитые колебания и волны 1 - тестирование	Все физические модели и задачи

По второй части в лаборатории студент должен выполнить 2 лабораторные работы по электричеству, 2 лабораторные работы по по магнитным полям и 1 лабораторную работу по электромагнитным волнам и колебаниям.

На каждом занятии студент может выполнить разное количество лабораторных работ по указанию преподавателя. В ходе компьютерного моделирования, должен решить задачи или ответить на вопросы к лабораторным работам. По каждой работе составляется отчет, в который входят результаты моделирования (расчеты и графики) и ответы на вопросы и решение задач. Отчет представляется в распечатанном на принтере или письменной форме в тетради (по указанию преподавателя) и сдается преподавателю на проверку.

Решение заданной задачи студент приводит в письменном виде с указанием примененных формул и математических расчетов!

Отчет по лабораторной работе сдается на проверку на следующем аудиторном занятии.

После того как студент выполнил лабораторные и контрольные работы, он допускается к тестированию. По результатам тестирования студент получает зачет или допускается к экзамену.

Требования к отчетам по лабораторным работам по физике

Отчеты по лабораторным работам должны содержать:

- наименование работы;

- цель работы;

- конспект основных законов, определений, понятий, формул;

- результаты компьютерного моделирования и расчетов (графики, рисунки, схемы);

- ответы на контрольные вопросы и подробное решение задач;

- выводы по результатам выполненной работы.

Список литературы

1. Трофимова Т.И. Курс физики. –М.: Высшая школа, 2001.

2. Савельев И.В. Курс общей физики. Т. 2. –М.: АСТ, 2003.

3. Сивухин Д.В. Общий курс физики. Т. 2. –М: Физматлит, 2002.

4. Грабовский Р.И. Курс физики. -6-е изд. – СПб.: Лань, 2002.

5. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. –М.: Академия, 2003.

Лабораторная работа 1
Электрическое поле

Краткая теория

Закон Кулона

Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие этого заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеется два вида электрических зарядов, условно называемых положительными и отрицательными. Заряды одного знака отталкиваются, разных знаков – притягиваются друг другом. Электрический заряд является неотъемлемым свойством некоторых элементарных частиц. Элементарный заряд е=1, 6∙ 10^-19 Кл. К числу элементарных частиц принадлежат, в частности, электрон (несущий отрицательный заряд –е), протон (несущий положительный заряд е) и нейтрон, его заряд равен нулю.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

(1.1)

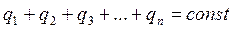Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

Закон, которому подчиняется сила взаимодействия точечных зарядов, был установлен экспериментально в 1785 г. Кулоном. С помощью крутильных весов Кулон измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов и от расстояния между ними (рис 1.1). При этом он исходил из того, что при касании к заряженному металлическому шарику точно такого же незаряженного заряд между ними распределяется поровну. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.

Рис 1.1

В результате своих опытов Кулон пришел к выводу, что сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряды прямой (рис 1.2).

(1.2)

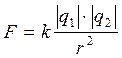Здесь k – коэффициент пропорциональности, который зависит от выбора системы единиц( в системе СИ , где ε ₀– электрическая постоянная; ε ₀=8, 85∙ 10^-12 Ф/м), q₁ и q₂ – величины взаимодействующих зарядов, r – расстояние между зарядами.

Рис 1.2

Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.2). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Опыт дает, что сила взаимодействия двух данных зарядов не изменяется, если вблизи них поместить еще какие-либо заряды. Силы кулоновского взаимодействия подчиняются принципу суперпозиции. Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел (рис 1.3).

(1.3)

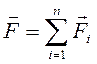
Рис. 1.3

Порядок выполнения работы

Упражнение №1

Теоретическая часть

Если изолированный проводник поместить в электрическое поле , то на свободные заряды q в проводнике будет действовать сила . В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, не скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника равно нулю. Однако, в проводниках может при определенных условиях возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δ q, переносимого через поперечное сечение проводника за интервал времени Δ t, к этому интервалу времени:

(2.1)

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю. Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачки жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток. При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы A_ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

(2.2)

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

(2.3)

Цепь постоянного тока можно разбить на определенные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными. При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δ φ ₁₂ = φ ₁ – φ ₂ между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе

₁₂, действующей на данном участке. Поэтому полная работа равна

(2.4)

Величину U₁₂ принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

(2.5)

Величину R принято называть электрическим сопротивлением. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

(2.6)

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

где l – длина проводника, S – площадь его поперечного сечения, ρ – зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением.

(2.7)

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры

Где α – температурный коэффициент сопротивления, зависящий от материала проводника.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:

(2.8)

Это выражение называется обобщенным законом Ома.

На рис. 2.1 изображена замкнутая цепь. Участок цепи (cd) является однородным. По закону Ома

(2.9)

Рис. 2.1.

Участок ab содержит источник тока с ЭДС, равной ε. Закон Ома для этого участка,

(2.10)

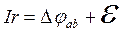Складывая равенства (2.9) и (2.10) получим

(2.11)

Но так как , получается что

(2.12)

Формула 2.12 выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника деленной на сумму сопротивлений однородного и неоднородного участков.

На рис. 2.2 дано схематическое изображение источника постоянного тока с ЭДС равной ε и внутренним сопротивлением r в трех режимах: «холостой ход» - цепь разомкнута(1), работа на нагрузку(2) и режим короткого замыкания(3). Указаны напряженность электрического поля внутри батареи и силы, действующие на положительные заряды: – электрическая сила и – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.

Рис.2.2.

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры. Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R_B. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 2.3, это условие записывается в виде:

Это условие означает, что ток I_B = Δ φ _cd / R_B, протекающий через вольтметр, много меньше тока I = Δ φ _cd / R₁, который протекает по узмеряемому участку цепи. Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.

(2.13)

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R_A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 2.3 сопротивление амперметра должно удовлетворять условию

чтобы при включении амперметра ток в цепи не изменялся.

Рис. 2.3

(2.14)

Проводники в электрических цепях могут соединяться последовательно и параллельно (рис. 2.4). При последовательном соединении проводников (рис. 2.4, а) сила тока во всех проводниках одинакова:

а) б)

Рис. 2.4.

(2.15)

По закону Ома, напряжения U₁ и U₂ на проводниках равны U₁ = IR₁, U₂ = IR₂. Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

U = U₁ + U₂ = I(R₁ + R₂) = IR,

(2.16)

где R – электрическое сопротивление всей цепи. Отсюда следует:

R = R₁ + R_2.

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.Этот результат справедлив для любого числа последовательно соединенных проводников.

(2.17)

При параллельном соединении (рис. 2.4, б) напряжения U₁ и U₂ на обоих проводниках одинаковы:

U₁ = U₂ = U.

(2.18)

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току I в неразветвленной цепи. Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δ t подтекает заряд IΔ t, а утекает от узла за то же время заряд I₁Δ t + I₂Δ t. Следовательно, I = I₁ + I₂. Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

(2.19)

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников. Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 2.5 приведен пример такой сложной цепи и указана последовательность вычислений.

Рис. 2.5.

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 2.6 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Рис. 2.6.

Обобщенный закон Ома позволяет рассчитать практически любую сложную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т.д.), довольно сложен. Эта задача решается более просто с помощью правил Кирхгофа.

Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом (рис 2.7).При этом ток входящий в узел, считается положительным, а ток выходящий из узла – отрицательным.

Рис 2.7.

(2.20)

Первое правило Кирхгофа: алгебраическая сумма токов сходящихся в узле, равна нулю:

Например, для рис. 2.7 первое правило Кирхгофа запишется так:

Первое правило вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 2.8 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d). В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.

Рис.2.8.

Второе правило Кирхгофа является следствием обобщенного закона Ома. Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 2.8, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 2.9.

Рис 2.9.

Для участков контура abcd обобщенный закон Ома записывается в виде:

для участка bc: I₁R₁ = Δ φ _bc – ₁; для участка da: I₂R₂ = Δ φ _da – ₂. Складывая левые и правые части этих равенств и принимая во внимание, что Δ φ _bc = – Δ φ _da, получим:

I₁R₁ + I₂R₂ = Δ φ _bc + Δ φ _da – ₁ + ₂ = – ₁ – _2.

Аналогично, для контура adef можно записать:

– I₂R₂ + I₃R₃ = ₂ + ₃.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

(2.21)

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным – его истинное направление противоположно выбранному.

2. Выбрать направление обхода контура и строго его придерживаться.

Составить столько уравнений, чтобы их число было равно числу искомых величин ( в систему уравнений должны входить все сопротивления и ЭДС рассматривамой цепи).

Порядок выполнения работы

Упражнение №1

Цепи постоянного тока

1) Включите компьютер. Загрузите пакет «Открытая физика 2.5» часть 2.

2) Выберите с помощью компьютерной мыши в содержании раздел «Постоянный электрический ток» на любую строку.

3) В верхнем правом углу расположено меню, которое содержит теорию, вопросы, задачи, задачи с решениями, лабораторные работы, журнал. Выберите раздел лабораторные работы обозначенный . Выберите лабораторную работу №1.2.

4) Перед Вами лабораторная работа №1.2. На рисунке представлено поле предназначенное для сборки различных электрических цепей (рис.2.10). Модель создавать электрические цепи используя различные комбинации соединений резисторов, измерительных приборов (амперметров и вольтметров) и источников ЭДС.

Рис.2.10

5) Составьте схему по указанию преподавателя.

6) Нажмите «Рассчитать». Модель покажет напряжения на различных участках цепи(рис.2.11).

Рис.2.11

7) Объясните полученные результаты.

8) Повторите моделирование несколько раз (с различными цепями по указанию преподавателя).

9) Зарисуйте схемы в тетрадь, запишите полученные результаты, либо распечатайте результат на принтере.

10) Ответьте на вопросы и решите задачи, предложенные к этой лабораторной работе.

10) Дома проработайте модель 1.6 из раздела «Модели».

11) Напишите вывод.

3. Контрольные вопросы

1. Назовите условия возникновения и существования электрического тока.

2. Что такое сторонние силы? Природа их возникновения.

3. В чем заключается физический смысл электродвижущей силы?

4. Что такое электрическое сопротивление? Как оно зависит от температуры?

5. Сформулируйте закон Ома: для однородного участка цепи; для неоднородного участка цепи.

6. Сформулируйте правила Кирхгофа.

7. Приведите пример расчета электрических цепей с помощью законов Ома и Кирхгофа.

Лабораторная работа №3

Магнитное поле вокруг проводников с токами

Краткая теория

Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда (1820 г.). Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов. По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.

Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера). Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако, опыт показывает, что изолированных магнитных зарядов не существует.

Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи). Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности электрического поля. Такой характеристикой является вектор магнитной индукции . Вектор магнитной индукции определяет силы, действующие на токи или движущиеся заряды в магнитном поле.

За положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора . Такое исследование позволяет представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 3.1.

Рис 3.1. Линии магнитной индукции полей постоянного магнита

и катушки с током.

Следует обратить внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.

Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции: е сли магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.

(3.1)

Индукцию проводника с током можно представить как векторную сумму элементарных индукций , создаваемых отдельными участками проводника. На опыте невозможно осуществить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад в магнитную индукцию результирующего магнитного поля, создаваемый малым участком Δ l проводника с током I.

(3.2)

здесь r - расстояние от данного участка Δ l до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ ₀ – постоянная величина, которую называют магнитной постоянной, μ ₀ = 4π ·10^–7 Н/ A² = 4π ·10^–7Гн/м.

Рис. 3.2. Иллюстрация закона Био-Савара

12 3 4 5 Следующая ⇒