Расчет средней проницаемости пласта при линейной фильтрации для изолированных зон
Теория к разделу
Слои и участки расположены параллельно. Допустим, длина и ширина у них одинаковые, а мощности пропластков (высоты) различны, вид фильтрации линейный:

Средняя проницаемость пласта оценивается выражением:
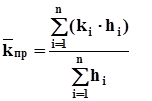 , (2.4) , (2.4)
где 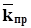 – средняя проницаемость пласта; – средняя проницаемость пласта;
ki – проницаемость i-го пропластка;
hi – мощность (высота) i-го пропластка.
Типовая задача
Рассчитать среднюю проницаемость пласта для условий:
Дано:
| № участка
| hi, м
| ki, мД
| |
| 6, 0
|
| |
| 4, 5
|
| |
| 3, 0
|
| |
| 1, 5
|
|
Найти: 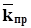
Решение:
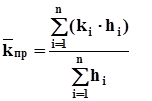 , ,
 . .
2.2.2. Задания для самостоятельной работы
Рассчитать среднюю проницаемость 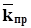 неоднородного пласта, имеющего i- изолированных пропластков, мощностью (высотой) hi, с проницаемостью ki для горизонтально-линейной фильтрации: неоднородного пласта, имеющего i- изолированных пропластков, мощностью (высотой) hi, с проницаемостью ki для горизонтально-линейной фильтрации:
hi - мощность i-го пропластка, м;
ki - проницаемость i-го пропластка, мД;
Ni - число пропластков;
1, ..., 120 - номер варианта.
Исходные данные представлены в таблице 2.2.
Таблица 2.2
| В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 0
|
| 2, 0
|
| 3, 0
|
| 1, 2
|
| 3, 8
|
| 6, 0
|
| 5, 0
|
| |
| 6, 0
|
| 3, 3
|
| 4, 5
|
| 1, 8
|
| 3, 6
|
| 5, 0
|
| 1, 2
|
| |
| 3, 0
|
| 2, 8
|
| 1, 5
|
| 1, 4
|
| 4, 0
|
| 0, 8
|
| 1, 6
|
| |
| 1, 2
|
| 1, 2
|
| 6, 0
|
| 6, 0
|
| 1, 2
|
| 1, 4
|
| 3, 8
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 8
|
| 1, 3
|
| 1, 5
|
| 8, 2
|
| 5, 0
|
| 8, 0
|
| 1, 3
|
| |
| 1, 6
|
| 4, 2
|
| 4, 2
|
| 1, 2
|
| 4, 5
|
| 6, 0
|
| 2, 4
|
| |
| 3, 2
|
| 6, 0
|
| 6, 2
|
| 1, 4
|
| 1, 2
|
| 1, 2
|
| 3, 2
|
| |
| 4, 8
|
| 1, 8
|
| 1, 4
|
| 6, 0
|
| 1, 5
|
| 1, 4
|
| 3, 8
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 4, 2
|
| 1, 4
|
| 1, 2
|
| 6, 0
|
| 1, 5
|
| 1, 2
|
| 1, 0
|
| |
| 4, 8
|
| 1, 6
|
| 0, 8
|
| 5, 0
|
| 4, 2
|
| 3, 8
|
| 3, 3
|
| |
| 2, 6
|
| 3, 6
|
| 1, 4
|
| 1, 8
|
| 1, 6
|
| 6, 0
|
| 4, 5
|
| |
| 5, 3
|
| 5, 0
|
| 3, 8
|
| 1, 3
|
| 4, 8
|
| 3, 6
|
| 6, 0
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 2, 0
|
| 5, 0
|
| 8, 0
|
| 4, 8
|
| 8, 0
|
| 1, 2
|
| 1, 4
|
| |
| 1, 2
|
| 1, 2
|
| 2, 0
|
| 2, 4
|
| 0, 5
|
| 2, 2
|
| 6, 0
|
| |
| 1, 8
|
| 1, 4
|
| 1, 2
|
| 1, 2
|
| 0, 9
|
| 1, 4
|
| 1, 8
|
| |
| 6, 0
|
| 3, 8
|
| 0, 9
|
| 1, 4
|
| 2, 7
|
| 3, 8
|
| 1, 4
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 5
|
| 1, 2
|
| 1, 2
|
| 1, 4
|
| 2, 0
|
| 4, 2
|
| 4, 8
|
| |
| 4, 0
|
| 1, 6
|
| 1, 4
|
| 6, 8
|
| 5, 0
|
| 5, 0
|
| 2, 4
|
| |
| 4, 2
|
| 6, 0
|
| 6, 0
|
| 3, 2
|
| 1, 8
|
| 1, 4
|
| 1, 2
|
| |
| 1, 6
|
| 3, 6
|
| 4, 5
|
| 4, 1
|
| 1, 2
|
| 2, 9
|
| 1, 4
|
|
Продолжение табл. 2.2
| В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 8, 0
|
| 4, 2
|
| 2, 8
|
| 1, 5
|
| 1, 8
|
| 1, 6
|
| 4, 6
|
| |
| 0, 5
|
| 4, 8
|
| 3, 6
|
| 1, 6
|
| 1, 9
|
| 1, 7
|
| 1, 7
|
| |
| 0, 9
|
| 1, 6
|
| 1, 5
|
| 1, 4
|
| 3, 6
|
| 1, 8
|
| 2, 9
|
| |
| 1, 1
|
| 1, 7
|
| 1, 6
|
| 1, 7
|
| 3, 4
|
| 2, 9
|
| 4, 2
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 0
|
| 2, 0
|
| 3, 0
|
| 1, 2
|
| 3, 8
|
| 6, 0
|
| 5, 0
|
| |
| 6, 0
|
| 3, 3
|
| 4, 5
|
| 1, 8
|
| 3, 6
|
| 5, 0
|
| 1, 2
|
| |
| 3, 0
|
| 2, 8
|
| 1, 5
|
| 1, 4
|
| 4, 0
|
| 0, 8
|
| 1, 6
|
| |
| 1, 2
|
| 1, 2
|
| 6, 0
|
| 6, 0
|
| 1, 2
|
| 1, 4
|
| 3, 8
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 4
|
| 8, 0
|
| 5, 0
|
| 8, 2
|
| 1, 5
|
| 1, 3
|
| 1, 8
|
| |
| 2, 4
|
| 6, 0
|
| 4, 5
|
| 1, 2
|
| 4, 2
|
| 4, 2
|
| 1, 6
|
| |
| 3, 2
|
| 1, 2
|
| 1, 2
|
| 1, 4
|
| 6, 2
|
| 6, 0
|
| 3, 2
|
| |
| 3, 8
|
| 1, 4
|
| 1, 5
|
| 6, 0
|
| 1, 4
|
| 1, 8
|
| 4, 8
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 4, 2
|
| 1, 4
|
| 1, 2
|
| 6, 0
|
| 1, 5
|
| 1, 2
|
| 1, 0
|
| |
| 4, 8
|
| 1, 6
|
| 0, 8
|
| 5, 0
|
| 4, 2
|
| 3, 8
|
| 3, 3
|
| |
| 2, 6
|
| 3, 6
|
| 1, 4
|
| 1, 8
|
| 1, 6
|
| 6, 0
|
| 4, 5
|
| |
| 5, 3
|
| 5, 0
|
| 3, 8
|
| 1, 3
|
| 4, 8
|
| 3, 6
|
| 6, 0
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 2, 0
|
| 5, 0
|
| 8, 0
|
| 4, 8
|
| 8, 0
|
| 1, 2
|
| 1, 4
|
| |
| 1, 2
|
| 1, 2
|
| 2, 0
|
| 2, 4
|
| 0, 5
|
| 2, 2
|
| 6, 0
|
| |
| 1, 8
|
| 1, 4
|
| 1, 2
|
| 1, 2
|
| 0, 9
|
| 1, 4
|
| 1, 8
|
| |
| 6, 0
|
| 3, 8
|
| 0, 9
|
| 1, 4
|
| 2, 7
|
| 3, 8
|
| 1, 4
|
|
Продолжение табл. 2.2
| В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 5
|
| 1, 2
|
| 1, 2
|
| 1, 4
|
| 2, 0
|
| 4, 2
|
| 4, 8
|
| |
| 4, 0
|
| 1, 6
|
| 1, 4
|
| 6, 8
|
| 5, 0
|
| 5, 0
|
| 2, 4
|
| |
| 4, 2
|
| 6, 0
|
| 6, 0
|
| 3, 2
|
| 1, 8
|
| 1, 4
|
| 1, 2
|
| |
| 1, 6
|
| 3, 6
|
| 4, 5
|
| 4, 1
|
| 1, 2
|
| 2, 9
|
| 1, 4
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 5
|
| 1, 2
|
| 1, 2
|
| 1, 4
|
| 2, 0
|
| 4, 2
|
| 4, 8
|
| |
| 0, 5
|
| 4, 8
|
| 3, 6
|
| 1, 6
|
| 1, 9
|
| 1, 7
|
| 1, 7
|
| |
| 4, 2
|
| 6, 0
|
| 6, 0
|
| 3, 2
|
| 1, 8
|
| 1, 4
|
| 1, 2
|
| |
| 6, 0
|
| 3, 8
|
| 0, 9
|
| 1, 4
|
| 2, 7
|
| 3, 8
|
| 1, 4
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 5
|
|
|
| 3, 8
|
| 1, 3
|
|
|
| 1, 2
|
|
|
| |
| 0, 5
|
| 3, 3
|
|
|
| 4, 2
|
| 2, 4
|
|
|
| 1, 2
|
| |
| 4, 2
|
| 1, 5
|
| 1, 6
|
| 1, 4
|
| 2, 6
|
| 1, 6
|
| 1, 4
|
| |
| 6, 0
|
|
|
| 4, 8
|
| 1, 5
|
|
|
| 3, 6
|
| 0, 9
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 4, 8
|
| 1, 5
|
|
|
| 4, 2
|
| 1, 6
|
|
|
|
|
| |
| 0, 5
|
| 1, 6
|
|
|
| 3, 6
|
| 1, 7
|
| 1, 8
|
| 2, 4
|
| |
| 1, 4
|
|
|
| 1, 2
|
| 1, 4
|
|
|
|
|
| 1, 2
|
| |
| 1, 8
|
| 4, 1
|
| 1, 1
|
| 3, 4
|
| 1, 2
|
| 1, 4
|
| 1, 5
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 8, 2
|
| 4, 2
|
| 1, 5
|
|
|
| 1, 2
|
| 1, 2
|
| 4, 8
|
| |
| 4, 2
|
| 1, 6
|
| 3, 8
|
|
|
|
|
| 6, 8
|
| 0, 5
|
| |
|
|
| 1, 4
|
| 4, 5
|
| 1, 2
|
| 4, 2
|
| 1, 8
|
|
|
| |
| 4, 8
|
| 1, 3
|
|
|
| 2, 7
|
| 3, 6
|
| 2, 9
|
| 0, 9
|
|
Продолжение табл. 2.2
| В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
| 1, 4
|
| 3, 8
|
| 1, 4
|
| 3, 8
|
| 3, 8
|
| 1, 0
|
| 1, 2
|
| |
| 1, 9
|
| 1, 2
|
|
|
| 1, 2
|
| 1, 8
|
| 3, 8
|
| 4, 2
|
| |
| 1, 2
|
| 4, 5
|
| 1, 6
|
| 2, 4
|
|
|
| 1, 6
|
| 1, 8
|
| |
| 1, 3
|
| 8, 2
|
| 4, 2
|
|
|
| 1, 2
|
| 1, 3
|
| 3, 8
|
| | В
|
|
|
|
|
|
|
| | Ni
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| hi
| ki
| |
|
|
| 1, 2
|
| 1, 4
|
| 1, 4
|
| 1, 2
|
|
|
| 4, 8
|
| |
| 1, 2
|
| 1, 6
|
| 4, 8
|
| 2, 2
|
| 0, 5
|
| 2, 4
|
|
|
| |
| 3, 6
|
| 2, 6
|
| 3, 3
|
| 2, 7
|
| 1, 2
|
| 1, 2
|
| 1, 4
|
| |
| 5, 3
|
| 3, 3
|
| 3, 6
|
| 1, 4
|
| 0, 9
|
| 3, 5
|
| 2, 4
|
| | В
|
| | | Ni
| hi
| ki
| | |
|
|
| | |
| 1, 2
|
| | |
| 1, 8
|
| | |
| 3, 8
|
| |
Расчет средней проницаемости пласта при радиальной фильтрации для изолированных зон
Теория к разделу
Слои и участки представляют собой цилиндрические дренируемые зоны, изолированные между собой. Если радиус скважины обозначить – rс, а радиус контура питания – rк, средняя проницаемость пласта оценивается выражением:
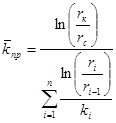 , (2.5) , (2.5)
где 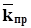 – средняя проницаемость пласта, мД; – средняя проницаемость пласта, мД;
ki – проницаемость зон, мД;
ri – радиус i-той зоны, м;
rс – радиус скважины, см;
rк – радиус контура питания, м.
Типовая задача
Рассчитать среднюю проницаемость пласта для условий:
Дано:
| № участка
| ri, м
| ki, мД
| | |
|
|
| rc = 15 см = 0, 15 м
| |
|
|
| |
|
|
| rk= 600 м
| |
|
|
| Найти: 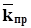
Решение:
 , ,
 . .
2.3.2. Задания для самостоятельной работы
Рассчитать среднюю проницаемость неоднородного пласта, состоящего из i – цилиндрических дренируемых, изолированных между собой зон, если радиус скважины – rс, радиус контура питания – rк; радиусы дренируемых зон – ri; с проницаемостью ki, мД:
ri – радиусы дренируемых зон, м;
ki – проницаемость дренируемых зон, мД;
rс – радиус скважины, см;
rк – радиус контура питания, м;
1, ..., 120 – номер варианта.
Исходные данные представлены в таблице 2.3.
Таблица 2.3
| В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| Продолжение табл. 2.3
| В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| Продолжение табл. 2.3
| В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| Продолжение табл. 2.3
| В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| Продолжение табл. 2.3
| В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | В
|
|
|
|
| | Ni
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| ri
| ki
|
| |
|
|
| rc=
|
|
| rc=
|
|
| rc=
|
|
| rc=
| |
|
|
|
|
|
|
|
|
| |
|
|
| rk=
|
|
| rk=
|
|
| rk=
|
|
| rk=
| |
|
|
|
|
|
|
|
|
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | Продолжение табл. 2.3
Популярное: - AT : химич. Природа, строение, свойства, механизм специфического взаимодействия с АГ
- AVC достигают макс. величины при этом объеме
- Aбстрактные классы, используемые при работе с коллекциями
- CПИСОК ТЕМ ДЛЯ РЕФЕРАТОВ, КУРСОВЫХ И ДИПЛОМНЫХ РАБОТ
- DOUBLE NEEDS PANG PANG ТУШЬ ДЛЯ РЕСНИЦ от TONY MOLY – 660 руб
- E) для факторов - капитал и земля
- E) может быть необъективным, сохраняя беспристрастность
- E) Способ взаимосвязанной деятельности педагога и учащихся, при помощи которого достигается усвоение знаний, умений и навыков, развитие познавательных процессов, личных качеств учащихся.
- Else write('не принадлежит')
- else write('не принадлежит')
- Gerund переводится на русский язык существительным, деепричастием, инфинитивом или целым предложением.
- I Чемпионат России по керлингу. Сезон 1992-1993гг (Мужчины)
|

