Линейные операции над векторами
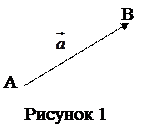 Вектором (свободным) называют совокупность всех одинаково направленных отрезков, имеющих одинаковую длину. Пусть
Вектором (свободным) называют совокупность всех одинаково направленных отрезков, имеющих одинаковую длину. Пусть 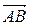 – направленный отрезок с началом в точке А и концом в точке В (рисунок 1). Этот отрезок
– направленный отрезок с началом в точке А и концом в точке В (рисунок 1). Этот отрезок 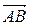 однозначно определяет некоторый вектор
однозначно определяет некоторый вектор  . В дальнейшем вектор
. В дальнейшем вектор  и направленный отрезок
и направленный отрезок 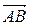 будут отождествляться, а использоваться будет тот из них, который в данном случае удобнее. Итак
будут отождествляться, а использоваться будет тот из них, который в данном случае удобнее. Итак  . Длина вектора
. Длина вектора  есть длина соответствующего отрезка
есть длина соответствующего отрезка 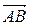 и обозначается
и обозначается  .
.
1.1.1 Определение. Векторы  и
и  называются коллинеарными, если соответствующие им направленные отрезки параллельны. Векторы
называются коллинеарными, если соответствующие им направленные отрезки параллельны. Векторы  ,
,  ,
, 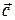 называются компланарными, если соответствующие им направленные отрезки параллельны одной плоскости.
называются компланарными, если соответствующие им направленные отрезки параллельны одной плоскости.
Два вектора  и
и  равны, если они коллинеарны, одинаково направлены и равны по длине. Пишут
равны, если они коллинеарны, одинаково направлены и равны по длине. Пишут  =
=  .
.
1.1.2 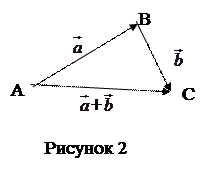 Определение. Суммой векторов
Определение. Суммой векторов  и
и 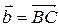 называется вектор, обозначаемый
называется вектор, обозначаемый  +
+  и равный
и равный 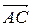 (рисунок 2).
(рисунок 2).
Итак, 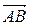 +
+ 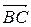 =
= 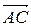 (правило треугольника).
(правило треугольника).
При решении задач полезно использовать свойства суммы векторов.
1.1.3  +
+  =
=  +
+  ,
, 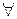
 ,
,  .
.
1.1.4  + (
+ (  +
+ 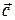 ) = (
) = (  +
+  )+
)+ 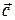 ,
, 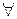
 ,
,  ,
, 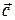 .
.
1.1.5 Существует единственный нулевой вектор  , имеющий нулевую длину и такой, что
, имеющий нулевую длину и такой, что 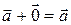 ,
, 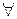
 .
.
1.1.6 Для любого вектора  существует единственный противоположный вектор (–
существует единственный противоположный вектор (–  ) такой, что
) такой, что 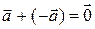 .
.
1.1.7 Определение. Произведением вектора  на действительное число
на действительное число 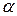 называется вектор
называется вектор 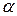
 (или
(или 
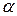 ), длина которого равна
), длина которого равна 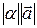 , а направление совпадает с направлением
, а направление совпадает с направлением  , если
, если 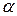 > 0, и противоположно
> 0, и противоположно  , если
, если 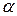 < 0.
< 0.
Перечислим свойства произведения вектора на число, которые постоянно используются при решении задач:
1) 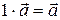 ; ;
| 3) 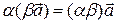 ; ;
| 5) 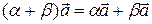 ; ;
|
2) 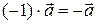 ; ;
| 4) 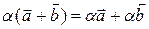 ; ;
| для любых 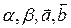 . .
|
1.1.8 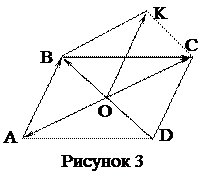 Пример. Пусть задан параллелограмм
Пример. Пусть задан параллелограмм 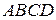 ,
, 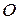 – точка пересечения его диагоналей (рисунок 3). Доказать, что
– точка пересечения его диагоналей (рисунок 3). Доказать, что
1) 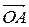 +
+ 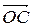 =
= 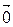 ; 3)
; 3) 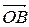 +
+ 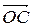 =
= 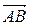 .
.
2) 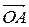 +
+ 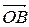 +
+ 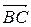 =
= 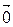 ;
;
Решение.
1 Известно, что диагонали параллелограмма вточке пересечения делятся пополам. Значит, 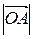 =
= 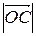 . Поскольку векторы
. Поскольку векторы 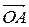 и
и 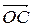 противоположно направлены, то
противоположно направлены, то 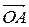 =−
=− 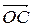 , т.е.
, т.е. 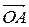 +
+ 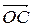 =
= 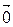 .
.
2 По определению суммы векторов 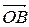 +
+ 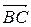 =
= 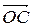 . С другой стороны
. С другой стороны 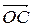 =−
=− 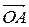 , поэтому
, поэтому 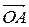 +
+ 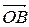 +
+ 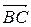 =
= 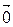 .
.
3 На векторах 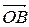 и
и 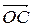 , как на сторонах, построим параллелограмм
, как на сторонах, построим параллелограмм 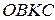 (см. рисунок 3). Тогда
(см. рисунок 3). Тогда 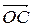 =
= 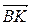 ,
, 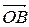 +
+ 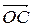 =
= 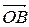 +
+ 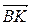 =
= 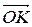 . Обратимся к четырехугольнику
. Обратимся к четырехугольнику 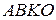 . Это параллелограмм, т.к.
. Это параллелограмм, т.к. 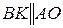 , и поэтому
, и поэтому 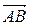 =
= 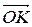 . Теперь очевидно, что
. Теперь очевидно, что 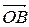 +
+ 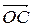 =
= 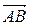 .
.
Линейная зависимость и независимость векторов
1.2.1 Определение. Векторы 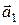 ,
,  , …,
, …, 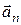 называются линейно зависимыми, если существуют числа
называются линейно зависимыми, если существуют числа 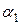 ,
, 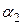 , …,
, …,  , не равные одновременно нулю, для которых выполняется равенство
, не равные одновременно нулю, для которых выполняется равенство
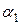
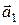 +
+ 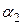
 + … +
+ … + 
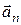 =
=  . (1)
. (1)
Если же равенство (1) выполняется только для 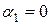 ,
, 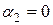 , …,
, …, 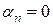 , то векторы
, то векторы 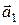 ,
,  , …,
, …, 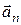 называются линейно независимыми.
называются линейно независимыми.
Основной признак, которым полезно пользоваться при установлении линейной зависимости (независимости) векторов, заключается в следующем.
1.2.2 Теорема. Векторы 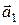 ,
,  , …,
, …, 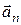 линейно зависимы тогда и только тогда, когда один из них является линейной комбинацией остальных.
линейно зависимы тогда и только тогда, когда один из них является линейной комбинацией остальных.
1.2.3 Пример. Пусть  и
и  – ненулевые векторы. Тогда следующие условия равносильны.
– ненулевые векторы. Тогда следующие условия равносильны.
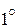 Векторы
Векторы  и
и  линейно зависимы.
линейно зависимы. 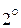
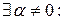
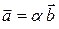 .
. 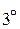
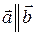 .
.
Доказательство проведем по схеме 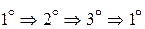 .
.
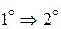 . Если
. Если  и
и 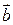 линейно зависимы, то существуют числа
линейно зависимы, то существуют числа 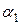 и
и 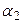 , такие, что
, такие, что 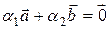 . Так как
. Так как  и
и  – ненулевые векторы, то в этом равенстве
– ненулевые векторы, то в этом равенстве 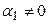 и
и 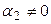 и из него получим
и из него получим 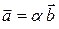 , где
, где 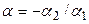 .
.
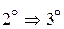 . Из равенства
. Из равенства 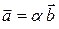 и условия
и условия 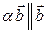 следует, что
следует, что 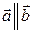 .
.
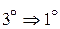 . Пусть
. Пусть 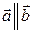 . Умножим вектор
. Умножим вектор 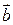 на число
на число 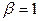 , если
, если  и
и  одинаково направлены, и на
одинаково направлены, и на  , если
, если  и
и  направлены противоположно. Тогда векторы
направлены противоположно. Тогда векторы  и
и 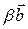 , имеющие одинаковые длины, равны, т.е.
, имеющие одинаковые длины, равны, т.е. 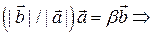
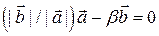 , что означает линейную зависимость векторов
, что означает линейную зависимость векторов  и
и  .
.
Таким образом, любые два коллинеарных вектора линейно зависимы. То же самое можно сказать о любых трех компланарных векторах.
Упражнения
1.3.1 Построить векторы  +
+  и
и  –
–  , если:
, если:
1.3.2 Проверить геометрически справедливость следующих равенств:
1) (  +
+  )+(
)+(  –
–  )=2
)=2  ; 3)
; 3) 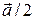 +
+ 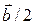 = (
= (  +
+  )/2;
)/2;
2) (  +
+  )– (
)– (  –
–  )=2
)=2  ; 4) (
; 4) (  –
–  )/2+
)/2+  = (
= (  +
+  )/2.
)/2.
1.3.3 Найти условия, которым должны удовлетворять векторы  и
и  , если:
, если:
1) 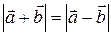 ; 2)
; 2) 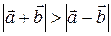 ; 3)
; 3) 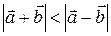 .
.
1.3.4 Пусть 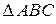 – произвольный треугольник, К, L, М – середины сторон
– произвольный треугольник, К, L, М – середины сторон 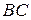 ,
, 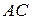 ,
,  соответственно,
соответственно, 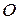 – точка пересечения медиан этого треугольника. Доказать, что
– точка пересечения медиан этого треугольника. Доказать, что
1) 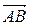 =
= 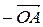 +
+ 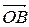 ; 3)
; 3) 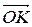 +
+ 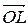 +
+ 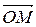 =
= 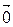 ;
;
2) 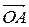 +
+ 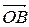 +
+ 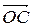 =
= 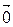 ; 4)
; 4) 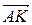 +
+ 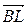 +
+ 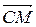 =
= 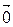 .
.
1.3.5 Дан параллелограмм 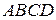 . Пусть
. Пусть 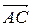 =
= 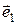 ,
, 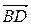 =
= 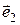 . Выразить векторы
. Выразить векторы 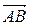 ,
, 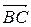 ,
, 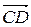 ,
, 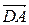 через векторы
через векторы 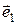 ,
, 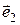 .
.
1.3.6 Доказать, что векторы 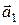 ,
,  , …,
, …, 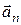 линейно зависимы, если хотя бы один из них нулевой.
линейно зависимы, если хотя бы один из них нулевой.
1.3.7 Доказать, что если некоторое непустое подмножество векторов из множества 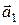 ,
,  , …,
, …, 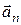 линейно зависимо, то и все векторы в целом линейно зависимы.
линейно зависимо, то и все векторы в целом линейно зависимы.
1.3.8 Доказать, что векторы 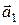 ,
,  , …,
, …, 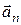 линейно зависимы, если среди них есть хотя бы два противоположных вектора.
линейно зависимы, если среди них есть хотя бы два противоположных вектора.
1.3.9 Доказать, что если векторы 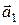 ,
,  , …,
, …, 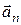 линейно независимы, то любое непустое подмножество из них также линейно независимо.
линейно независимы, то любое непустое подмножество из них также линейно независимо.
1.4 Контрольные задания
Рекомендуемая литература [1, гл. 1, §1], [2, гл. 2, §§2.1–2.4], [3, гл. I, §1.3].
1.4.1 Выбрать два произвольных неколлинеарных вектора  ,
,  и построить вектор
и построить вектор 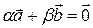 , где
, где
1) 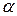 =1,
=1, 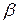 =1; 2)
=1; 2) 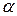 = –1,
= –1, 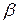 =1; 3)
=1; 3) 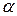 = –1,
= –1, 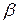 = –1; 4)
= –1; 4) 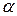 = –
= – 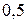 ,
, 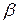 =3.
=3.
1.4.2 Пусть 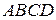 – параллелограмм,
– параллелограмм, 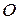 – точка пересечения его диагоналей АС и BD. Доказать, что
– точка пересечения его диагоналей АС и BD. Доказать, что
1) 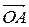 =
= 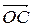 ; 3)
; 3) 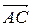 +
+ 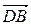 =
= 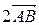 ;
;
2) 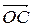 −
− 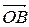 +
+ 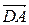 =
= 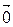 ; 4)
; 4) 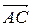 –
– 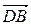 =
= 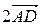 ;
;
5) 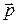 коллинеарен
коллинеарен 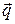 , где
, где 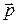 =2
=2 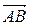 –3
–3 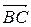 ,
, 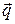 =
= 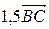 –
– 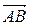 .
.
1.4.3 Пусть 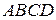 – произвольный четырехугольник,
– произвольный четырехугольник, 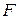 и
и 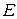 – середины сторон AB и CD соответственно. Доказать, что
– середины сторон AB и CD соответственно. Доказать, что 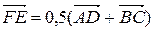 .
.
1.4.4 Пусть  – треугольник, М - точка пересечения его медиан, О – произвольная точка,
– треугольник, М - точка пересечения его медиан, О – произвольная точка, 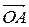 =
= 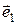 ,
, 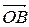 =
= 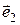 ,
, 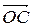 =
= 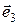 . Выразить вектор
. Выразить вектор 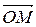 через векторы
через векторы 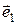 ,
, 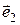 ,
, 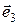 .
.
1.4.5 Доказать, что векторы 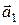 ,
,  , …,
, …, 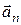 линейно зависимы, если хотя бы два на них равны.
линейно зависимы, если хотя бы два на них равны.
Популярное:

