Истечение через большое отверстие
При истечении из отверстия больших размеров в боковой стенке сосуда напор Н не будет одинаковым во всем сечении отверстия. Для точек нижней части сечения он будет большим, а в верхней – меньшим. Однако давление во всех точках вытекающей струи будет одинаковым (при истечении в атмосферу оно будет равно атмосферному давлению), что не соответствует распределению давления по гидростатическому закону. В связи с чем уравнение Бернулли здесь можно применить не ко всей струе в целом, а лишь к отдельным элементарным струйкам. Чтобы определить среднюю скорость истечения и расход жидкости, площадь поперечного сечения отверстия подразделяется на элементарные площади и для каждой из них находится элементарный расход. Полный расход определяется суммированием элементарных расходов по всему сечению.
Пусть a и b - высота и ширина бокового отверстия в тонкой стенке некоторой емкости (рис. 8.3). Разобьем площадь поперечного сечения отверстия на полоски высотой dz. Элементарный расход через такую полоску сечением dzb согласно формуле (8.1) будет
 , ,
где m - коэффициент расхода для малого отверстия.

Рис. 8.3
Принимая  и считая, что скорость на свободной поверхности и считая, что скорость на свободной поверхности  , получим , получим
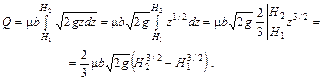 (8.2) (8.2)
Обозначая через H0 полный напор над центром тяжести отверстия, найдем  и и  . Разлагая члены вида . Разлагая члены вида  по формуле бинома Ньютона, будем иметь (ограничимся четырьмя членами разложения) по формуле бинома Ньютона, будем иметь (ограничимся четырьмя членами разложения)
 ; ;
 . .
Учитывая эти соотношения, выражение, заключенное в скобки в формуле (8.2), примет вид
 . (8.3) . (8.3)
Второй член в скобке обычно мал по сравнению с единицей и им можно пренебречь.
Тогда формула (8.2) с учетом (8.3) примет вид

или
 . (8.4) . (8.4)
Учитывая, что  , получим , получим
 , ,
где w - площадь сечения отверстия.
Эта формула имеет тот же вид, что и формула для определения расхода при истечении жидкости из малого отверстия в тонкой стенке (см § 8.1).
Допущения, принятые при выводе формулы (8.4), корректируются уточнением коэффициента расхода m. Как показывают опыты, этот коэффициент существенно зависит от формы, размеров отверстия и от напора. Так, с увеличением размеров отверстия коэффициент расхода уменьшается, а с увеличением напора уменьшается влияние размера отверстия на коэффициент расхода.
Истечение через затопленное отверстие
Рассмотрим открытый сосуд, разделенный перегородкой на два отделения с разными уровнями жидкости (рис. 8.4). В перегородке имеется отверстие, через которое жидкость перетекает из одной части сосуда в другую.
Требуется определить скорость истечения жидкости через отверстие и ее расход.
Составим уравнение Бернулли для сечений 1-1 и с-с (примем для простоты  ) )
 . .
Учитывая, что по формуле гидростатического давления

 и принимая и принимая  вследствие ее малости, получим вследствие ее малости, получим
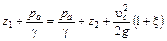 . .
Отсюда
 , ,
где  . .
Расход жидкости через отверстие определяется по формуле
 , (8.5) , (8.5)
где 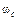 - площадь струи в узком сечении. - площадь струи в узком сечении.
Учитывая, что  (см. § 8.1), где (см. § 8.1), где  - площадь сечения отверстия, формула (8.5) будет - площадь сечения отверстия, формула (8.5) будет
 . .
Так как  , где m - коэффициент расхода, то , где m - коэффициент расхода, то
 . .
Опыт показывает, что коэффициент расхода m для затопленных и незатопленных отверстий практически одинаков.
Истечение жидкости при переменном напоре
Истечение при переменном напоре является, по сути дела, неустановившимся движением жидкости. Мы ограничимся лишь тем случаем, когда такое движение можно приближенно считать установившимся, то есть пренебречь силами инерции. Рассмотрим простейший случай опорожнения резервуара, имеющего площадь живого сечения W (рис.8.5).
Пусть начальный напор есть H1 и конечный H2. Расчет опорожнения заключается в определении времени этого процесса. Количество жидкости, вытекающее за время dt, равно
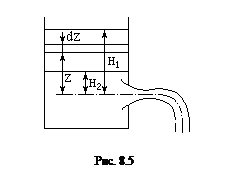  . .
С другой стороны,
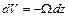 , ,
где знак минус взят потому, что dz - отрицательно, а dV принимаем положительным.
Тогда
 . .
Отсюда
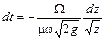 . .
Интегрируя, получим
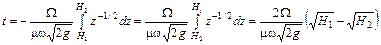 . .
Время полного опорожнения получим, положив H2 = 0.
 . .
Или
 , ,
где V - объем резервуара; Q - расход жидкости при начальном напоре H1.
То есть время опорожнения сосуда при переменном напоре в 2 раза больше того времени, которое требуется для вытекания жидкости при начальном напоре H1, в количестве, равном первичному объему V1.
ИСТЕЧЕНИЕ ЧЕРЕЗ НАСАДКИ
Насадком называется короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина патрубка  , где d диаметр отверстия. , где d диаметр отверстия.
Насадки делятся на 3 основных типа.
1. Цилиндрические (рис. 8.6, 8.7).
2. Конические (рис. 8.8, 8.9).
3. Коноидальные (рис. 8.10).
1. Цилиндрические насадки делятся на внешние (рис. 8.6) и внутренние (рис. 8.7).

При движении жидкости внутри насадка образуется сжатое сечение с-с, в области которого наблюдается вакуум. Образование вакуума объясняется тем, что скорость в сжатом сечении больше, чем скорость в месте выхода струи из насадка. Как показывает опыт, при применении цилиндрических насадок пропускная способность увеличивается по сравнению с тонким отверстием того же диаметра. Увеличение пропускной способности и является основным назначением этих насадок.
2. Конические насадки бывают 2-х типов - расходящиеся (рис. 8.8) и сходящиеся (рис. 8.9).

В конических расходящихся насадках также создается вакуум. При большом угле конусности возможен обрыв потока от стенок и насадок будет работать как обычное отверстие. Конические расходящиеся насадки имеют самые большие потери энергии. Отличительными особенностями расходящихся насадок являются: значительный вакуум, большая пропускная способность, малые скорости выхода. Они применяются там, где требуется значительный вакуум, например в инжекторах, а также там, где требуется малая скорость, например в дождевальных аппаратах.
Основным назначением конических сходящихся насадков является увеличение скорости выхода потока с целью создания большой кинетической энергии в струе. Конические сходящиеся насадки применяются в качестве сопел гидромониторов и активных гидротурбин, наконечников пожарных брандспойтов и в других устройствах.
 3. Коноидальные насадки представляют собой усовершенствованные конически сходящиеся насадки (рис. 8.10). Они выполняются по форме струи, выходящей из отверстия и поэтому потери энергии в них минимальные. 3. Коноидальные насадки представляют собой усовершенствованные конически сходящиеся насадки (рис. 8.10). Они выполняются по форме струи, выходящей из отверстия и поэтому потери энергии в них минимальные.
Коэффициент расхода коноидального насадка является наивысшим.
Гидравлический расчет насадков ведется по тем же формулам, что для отверстия в тонкой стенке
 , ,
где -  и и  . Только вместо коэффициента местных потерь ξ следует поставить в формулу для j суммарный коэффициент сопротивления . Только вместо коэффициента местных потерь ξ следует поставить в формулу для j суммарный коэффициент сопротивления
 , ,
где l - длина, d - диаметр насадка.
Оглавление
| Глава 1. Введение
|
| | § 1.1.
| Краткий исторический обзор развития гидравлики
|
| | § 1.2.
| Определение науки «Гидромеханика»
|
| | § 1.3.
| Реальные и идеальные жидкости
|
| | § 1.4.
| Размерности физических величин, применяемых в гидромеханике
|
| | Глава 2. Свойства жидкостей ………………………………
|
| | § 2.1.
| Основные физико-механические свойства жидкости ……………...
|
| | § 2.2.
| Вязкость. Закон Ньютона для внутреннего трения в жидкости
|
| | § 2.3.
| Зависимость вязкости от температуры и давления. Вискозиметры
|
| | Глава 3. Гидростатика ……………………………………………...
|
| | § 3.1.
| Силы, действующие в жидкости …………………………………….
|
| | § 3.2.
| Гидростатическое давление и его свойства ………………………...
|
| | § 3.3.
| Дифференциальные уравнения равновесия жидкости ……………..
|
| | § 3.4.
| Потенциал массовых сил …………………………………………….
|
| | § 3.5.
| Интеграл уравнений Эйлера для несжимаемой жидкости ………...
|
| | § 3.6.
| Уравнение поверхности равного давления …………………………
|
| | § 3.7.
| Основное уравнение гидростатики ………………………………….
|
| | § 3.8.
| Методы и приборы для измерения давления. Абсолютное и избыточное давление. Вакуум ……………………………………..
|
| | § 3.9.
| Гидростатический напор и энергетический закон для жидкости, находящейся в равновесии …………………………………………...
|
| | § 3.10.
| Интегрирование уравнений Эйлера для случая относительного покоя жидкости ……………………………………………………….
|
| | § 3.11.
| Сила давления жидкости на криволинейную поверхность произвольной формы …………………………………………………
|
| | § 3.12.
| Частные случаи расчета сил, действующих на криволинейные поверхности закономерных форм …………………………………...
|
| | § 3.13.
| Сила давления жидкости на плоскую стенку произвольной формы
|
| | § 3.14.
| Гидростатический парадокс ………………………………………….
|
| | § 3.15.
| Центр давления и определение его координат ……………………..
|
| | § 3.16.
| Простые гидравлические машины. Гидравлический пресс ………..
|
| | § 3.17.
| Гидравлический аккумулятор ………………………………………..
|
| | § 3.18.
| Закон Архимеда ……………………………………………………....
|
| | § 3.19.
| Условия плавучести и остойчивости тел, частично погруженных в жидкость …………………………………………………………….
|
| | Глава 4. Гидродинамика …………………………………………...
|
| | § 4.1.
| Основные кинематические понятия и определения. Два метода исследования жидкости ………………………………...
|
| | § 4.2.
| Траектории частиц и линии тока …………………………………….
|
| | § 4.3.
| Установившееся движение …………………………………………..
|
| | § 4.4.
| Струйчатая модель движения жидкости. Трубка тока. Расход жидкости ……………………………………………………..
|
| | § 4.5.
| Средняя скорость ……………………………………………………..
|
|
| § 4.6.
| Уравнение неразрывности в переменных Эйлера в декартовой системе координат ……………………………………………………
|
| | § 4.7.
| Дифференциальные уравнения движения идеальной (невязкой) жидкости (уравнения Эйлера) ……………………………………….
|
| | § 4.8.
| Дифференциальные уравнения движения вязкой жидкости (уравнения Навье-Стокса) ……………………………………………
|
| | § 4.9.
| Уравнение Бернулли для элементарной струйки идеальной жидкости ………………………………………………………………
|
| | § 4.10.
| Физический и геометрический смысл уравнения Бернулли. Напор жидкости ………………………………………………………
|
| | § 4.11.
| Уравнение Бернулли для элементарной струйки реальной жидкости ………………………………………………………………
|
| | § 4.12.
| Уравнение Бернулли для потока реальной жидкости ……………...
|
| | § 4.13.
| Графическая иллюстрация уравнения Бернулли для потока реальной жидкости …………………………………………………...
|
| | § 4.14.
| Практическое применение уравнения Бернулли …………………...
|
| | § 4.15.
| Трубка Прандтля ……………………………………………………...
|
| | § 4.16.
| Трубка Вентури, сопло, диафрагма ………………………………….
|
| | Глава 5. Основы теории гидродинамического подобия ………..
|
| | § 5.1.
| Основные понятия и определения теории подобия ………………...
|
| | § 5.2.
| Теоремы теории подобия. Критерии подобия ……………………...
|
| | § 5.3.
| Физический смысл критериев подобия ……………………………..
|
| | § 5.4.
| Метод анализа размерности …………………………………………
|
| | Глава 6. Классификация гидравлических потерь. Режимы течения жидкости ………………………………………...
|
| | § 6.1.
| Два режима движения жидкости …………………………………….
|
| | § 6.2.
| Равномерное движение жидкости …………………………………...
|
| | § 6.3.
| Основное уравнение равномерного потока. Уравнение динамического равновесия равномерного потока ………………….
|
| | § 6.4.
| Ламинарное движение жидкости ……………………………………
|
| | § 6.5.
| Расход жидкости ……………………………………………………...
|
| | § 6.6.
| Коэффициент линейных потерь при ламинарном движении жидкости ………………………………………………………………
|
| | § 6.7.
| Формирование изотермического ламинарного потока …………….
|
| | § 6.8.
| Основы гидродинамической теории смазки ………………………..
|
| | § 6.9.
| Турбулентное движение жидкости ………………………………….
|
| | § 6.10.
| Турбулентное перемешивание. Пульсация скоростей и напряжений при турбулентном режиме …………………………..
|
| | § 6.11.
| Осреднение скоростей ………………………………………………..
|
| | § 6.12.
| Осреднение напряжений ……………………………………………..
|
| | § 6.13.
| Структура турбулентного потока ……………………………………
|
| | § 6.14.
| Касательные напряжения в турбулентном потоке …………………
|
| | § 6.15.
| Полуэмпирические теории турбулентности ……………………….
|
| | § 6.16.
| Логарифмический закон распределения скоростей в круглой трубе
|
|
| § 6.17.
| Экспериментальные данные для коэффициента гидравлического сопротивления. Опыты Никурадзе и Зегжда ………………………….….
|
| | § 6.18.
| Формулы для определения коэффициента гидравлического сопротивления ………………………………………………………...
|
| | § 6.19.
| Местные сопротивления ……………………………………………..
|
| | § 6.20.
| Зависимость коэффициента местных потерь от числа Рейнольдса
|
| | § 6.21.
| Принцип наложения потерь напора. Коэффициент
сопротивления системы ……………………………………………...
|
| | § 6.22.
| Основные расчетные формулы для определения потерь напора …
|
| | Глава 7. Гидравлический расчет трубопроводов ………………………
|
| | § 7.1.
| Назначение и классификация трубопроводов ………………………
|
| | § 7.2.
| Расчет и проектирование трубопроводов …………………………...
|
| | § 7.3.
| Гидравлический расчет простого трубопровода …………………...
|
| | § 7.4.
| Метод эквивалентных потерь ……………………………………….
|
| | § 7.5.
| Гидравлический расчет сложных трубопроводов ………………….
|
| | § 7.6.
| Гидравлические характеристики трубопроводов …………………..
|
| | § 7.7.
| Гидроэнергетический баланс насосной установки …………………
|
| | § 7.8.
| Сифонные трубопроводы …………………………………………….
|
| | § 7.9.
| Гидравлический удар в трубах ………………………………………
|
| | § 7.10.
| Кавитация ……………………………………………………………..
|
| | Глава 8. Истечение жидкости через отверстия и насадки …………….
|
| | § 8.1.
| Истечение через малое отверстие в тонкой стенке ………………...
|
| | § 8.2.
| Истечение через большое отверстие ……………………………….
|
| | § 8.3.
| Истечение через затопленное отверстие ……………………………
|
| | § 8.4.
| Истечение жидкости при переменном напоре ……………………..
|
| | § 8.5.
| Истечение через насадки …………………………………………….
|
| |
| Приложения ………………………………………………….………..
|
| |
| Библиографический список ………………………………………….
|
|
ПРИЛОЖЕНИЯ
Таблица П1
Средние значения плотности ρ и кинематической
вязкости v некоторых жидкостей
| Жидкости
| Плотность r,
кг/м3 при Т, оС
| Кинематическая вязкость n, Ст при Т, оС
| |
|
|
|
|
|
| | Вода пресная
Нефть Баку, легкая
Нефть Баку, тяжелая
Бензин авиационный
Керосин Т-1(очищен.)
Керосин Т-2(трактор.)
Дизельное топливо
Глицерин
Ртуть
Масла:
Касторовое
Трансформаторное
АМГ-10
Веретенное АУ
Индустриальное 12
Индустриальное 20
Индустриальное 30
Индустриальное 50
Турбинное
|
-
-
-
-
-
-
-
| -
-
-
-
-
-
-
-
-
-
| 0, 010
0, 25
1, 4
0, 0073
0, 025
0, 010
0, 28
9, 7
0, 0016
0, 28
0, 17
0, 48
0, 48
0, 85
1, 8
5, 3
0, 97
| 0, 0065
-
-
0, 0059
0, 018
-
0, 12
3, 3
0, 0014
3, 5
0, 13
0, 11
0, 19
0, 19
0, 33
0, 56
1, 1
0, 38
| 0, 0047
-
-
0, 0049
0, 012
-
-
0, 88
0, 0010
0, 88
0, 078
0, 085
0, 098
0, 098
0, 14
0, 21
0, 38
0, 16
| 0, 0036
-
-
0, 010
-
-
0, 38
-
0, 25
0.048
0, 065
0, 099
0, 059
0, 080
0, 11
0, 16
0, 088
|
Таблица П2
Давление насыщенного пара pп воды
| Температура T, 0C
| 0, 0
| 5, 00
| 10, 0
| 20, 0
| 30, 0
| 40, 0
| 50, 0
| 60, 0
| 80, 0
| | Давление, кПа
| 0, 588
| 0, 882
| 1, 18
| 2, 35
| 4, 19
| 7, 29
| 12, 1
| 19, 6
| 46, 0
|
Таблица П3
Плотность и кинематическая вязкость воды и воздуха (p = 98 кПа)
| Температура, 0С
| r, кг/м3
| n× 106, м2/с
| r, кг/м3
| n× 106, м2/с
| | для воды
| для воздуха
| |
| 999, 87
1000, 0
999, 73
998, 23
995, 76
992, 24
998, 07
983, 24
997, 81
971, 83
965, 34
953, 38
| 1, 79
1, 65
1, 31
1, 01
0, 81
0, 60
0, 56
0, 48
0, 42
0, 37
0, 33
0, 29
| 1, 28
1, 26
1, 23
1, 185
1, 150
1, 110
1, 080
1, 045
1, 020
0, 990
0, 960
0, 935
| 13, 7
14, 1
14, 7
15, 7
16, 6
17, 6
18, 6
19, 6
20, 45
21, 7
22, 9
23, 8
|
Таблица П4
Зависимость коэффициента температурного расширения
воды bt от температуры
| t,
0C
| bt × 106, 0C-1 при p, Па× 105
| | 1, 0
| 2, 0
| 5, 0
| 9, 0
| | 1-10
10-20
40-50
60-80
90-100
|
|
—
|
|
|
Таблица П5
Зависимость коэффициента температурного сжатия
воды bp от температуры
| t,
0C
| bp × 106, Па-1 при p, Па× 105
| | 0, 5
| 1, 0
| 2, 0
| 3, 0
| |
| 5, 40
5, 29
5, 23
5, 18
5, 15
| 5, 37
5, 23
5, 18
5, 10
5, 05
| 5, 31
5, 18
5, 08
5, 03
4, 95
| 5, 23
5, 08
4, 98
4, 88
4, 81
|
Таблица П6
Популярное:
|

