Теорема Остроградского–Гаусса и ее применение к расчету полей

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Вычисление электрического поля во многих случаях сильно упрощается применением теоремы, которая была установлена М.В.Остроградским в виде некоторой общей математической теоремы и Гауссом – применительно к случаю электрического поля, создаваемого точечным зарядом, через замкнутую шаровую поверхность .

Значение проекции вектора напряженности на поверхности сферы радиуса R:

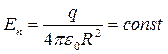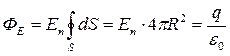
Выразим поток вектора через любую замкнутую поверхность. Он равен числу силовых линий, выходящих наружу, т.е. начинающихся на заряде.

Теперь допустим, что внутри замкнутой поверхности находятся N точечных зарядов q₁, q₂, …, q_N. В силу принципа суперпозиции: .

Если линия напряженности пересекает поверхность не один раз, а несколько, то обязательно нечетное число раз, так что в интеграле она будет учтена только один раз, и выражение сохранит силу и для этого случая. Таким образом, для электростатики теорема Остроградского–Гаусса формулируется следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε ₀.

Применим теорему Остроградского-Гаусса для расчета конкретных полей:

а) электрическое поле, создаваемое бесконечной однородно заряженной плоскостью

Пусть поверхностная плотность заряда . В качестве замкнутой поверхности, через которую вычислим величину потока вектора напряженности электрического поля выберем цилиндрическую поверхность, как показано на рисунке.

Из соображения симметрии (электрическое поле имеет плоскую симметрию) вытекает, что напряженность поля в любой точке имеет направление, перпендикулярное плоскости. Очевидно, что модуль напряженности в точках, симметричных относительно плоскости одинаков: E' = E" =E. Направление внешней нормали перпендикулярно заряженной поверхности.

Согласно теореме Гаусса: 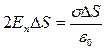. С учетом того, что получаем: . Напряженность электрического поля одинакова на любом расстоянии от плоскости.

б) электрическое поле, создаваемое двумя бесконечными заряженными плоскостями

Пусть поверхностная плотность заряда на каждой поверхности . В случае разноименно заряженных бесконечных плоскопараллельных пластин, как видно из рисунка, с учетом выражения для напряженности электрического поля, создаваемого бесконечно заряженной плоскости ( ).

Для пространства между пластинами 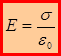; для пространства за пластинами (слева от левой и справа от правой пластины) .

В случае одноименно заряженных бесконечных плоскопараллельных пластин,

как видно из рисунка, для пространства за пластинами ; для пространства между пластинами .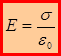

в) электрическое поле бесконечного заряженного цилиндра

Пусть поверхностная плотность заряда , R – радиус цилиндрической поверхности. В качестве замкнутой поверхности, через которую вычислим величину потока вектора напряженности электрического поля выберем цилиндрическую поверхность, как показано на рисунке. Из соображений симметрии (электрическое поле имеет осевую симметрию) напряженность электрического поля направлена перпендикулярно боковой поверхности замкнутой цилиндрической поверхности. Направление внешней нормали к боковой поверхности цилиндра по направлению является радиальным: . Откуда . С учетом E=E _n , имеем: пр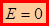и ; при ; при .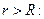

Или введя линейную плотность запишем теорему Остроградского-Гаусса . Откуда Учитывая, что , получаем выражение для определения величины напряженности электрического поля: Для различных областей пространства имеем: для (внутри данной области электрические заряды отсутствуют): ; для : ; для : .

г) поле заряженной сферической поверхности

Пусть поверхностная плотность заряда , R – радиус сферической поверхности. В качестве замкнутой поверхности, через которую вычислим величину потока вектора напряженности электрического поля, выберем сферическую поверхность, как показано на рисунке. Из соображений симметрии (электрическое поле имеет центральную симметрию) напряженность электрического поля направлена перпендикулярно сферической поверхности. Направление внешней нормали к сферической поверхности по направлению является радиальным. Используя теорему Остроградского-Гаусса, получаем: ; . С учетом E=E _n , имеем: для (внутри данной области электрические заряды отсутствуют) ; для ; для : .

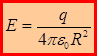Получим также выражение для напряженности электрического поля в случае, когда известна величина заряда q на сферической поверхности. Использование теоремы Остроградского-Гаусса дает следующий результат: . Откуда . С учетом E=E _n , имеем: для (внутри данной области электрические заряды отсутствуют) ; для : ; для : .

д) поле объемно-заряженного шара:

Пусть R – радиус шара. Из соображений симметрии (электрическое поле имеет центральную симметрию) напряженность электрического поля направлена перпендикулярно сферической поверхности. Направление внешней нормали к сферической поверхности по направлению является радиальным. Рассмотрим возможные случаи. Для случая 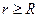в качестве замкнутой поверхности, через которую вычислим величину потока вектора напряженности электрического поля, выберем сферическую поверхность 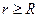, как показано на рисунке.

Используя теорему Остроградского-Гаусса, получаем:

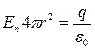. Откуда . С учетом E=E _n , имеем: дл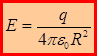я : ; для : .

Для случая в качестве замкнутой поверхности, через которую вычислим величину потока вектора напряженности электрического поля, выберем сферическую поверхность , как показано на рисунке.

При этом внутрь замкнутой поверхности попадает не весь электрический заряд шара, а лишь его часть. Для вычисления ее введем величину объемной плотности электрического заряда . Используя теорему Остроградского-Гаусса, получаем: 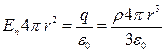, откуда: . Учитывая, что заряд шара , полученное выражение можно преобразовать: 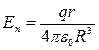. С учетом E=E _n , имеем: .

⇐ Предыдущая 123 4 Следующая ⇒