|
| ВОПРОС
|
| ОТВЕТ
|
|
| Длина звуковой волны λ. связана со скоростью распространения волны V и частотой колебаний ν соотношением:
|
| 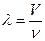 или λ = VT,
где Т — период колебания. или λ = VT,
где Т — период колебания.
|
|
| При переходе звуковой волны из одной среды в другую отношение скорости звука к длине волны остается
|
| постоянным, т. е.
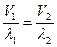 ,
где V1, λ 1 и V2, λ 2 — соответственно скорости и длины волн в первой и второй средах ,
где V1, λ 1 и V2, λ 2 — соответственно скорости и длины волн в первой и второй средах
|
|
| По принципу Доплера частота звука v1 воспринимаемая наблюдателем, связана с частотой звука v0, создаваемой источником звука, соотношением
|
| 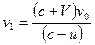 ,
где с — скорость распространения звука в среде; V — скорость движения наблюдателя относительно земли (V > 0, если наблюдатель движется к источнику звука, и V< 0, если удаляется от него); и — скорость движения источника относительно земли (u> 0, если источник звука движется к наблюдателю, и u< 0, если удаляется от него). ,
где с — скорость распространения звука в среде; V — скорость движения наблюдателя относительно земли (V > 0, если наблюдатель движется к источнику звука, и V< 0, если удаляется от него); и — скорость движения источника относительно земли (u> 0, если источник звука движется к наблюдателю, и u< 0, если удаляется от него).
|
|
| Доплеровский сдвиг частоты
|
| 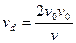 где v0 — скорость движущегося тела, v — скорость волны (ультразвука). Формула получена в предположении v> v0.
где v0 — скорость движущегося тела, v — скорость волны (ультразвука). Формула получена в предположении v> v0.
|
|
| Волновым сопротивлением среды называют
|
| произведение плотности среды ρ, в которой распространяется звук, на скорость звука V в этой среде:
Z=ρ V
|
|
| Амплитудное значение звукового давления для чистого тона можно определить по формуле
|
| 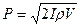 ,
где I — интенсивность звука; ρ — плотность среды; V — скорость звука в среде. ,
где I — интенсивность звука; ρ — плотность среды; V — скорость звука в среде.
|
|
| Уровень интенсивности звука L относительно условного нулевого уровня, соответствующего интенсивности I0, определяется на основании психофизического закона Вебера — Фехнера:
|
| 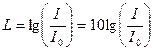 ,
где I0 — условная интенсивность для звука с частотой 1000 гц на пороге слышимости (пороговая интенсивность раздрожителя), равная 10-12 Bт/м2; I — интенсивность (надпороговая интенсивность) исследуемого звука. ,
где I0 — условная интенсивность для звука с частотой 1000 гц на пороге слышимости (пороговая интенсивность раздрожителя), равная 10-12 Bт/м2; I — интенсивность (надпороговая интенсивность) исследуемого звука.
|
|
| Закон В.Фехнера
|
| ν =klog(I/I0), где ν - силовая функция
|
|
| Психофизический закон Стивенса
|
| ν = k(I-I0)n, где n- константа, разная у различных рецепторов. Обычно n< 1.
|
|
| Ощущение, возникающее при слуховом восприятии звука, характеризуется
|
| уровнем громкости
|
|
| Уровень громкости данного звука принимается равным
|
| уровню интенсивности равногромкого с ним эталонного звука частотой 1000 гц.
|
|
| Уровень интенсивности и интенсивность характеризуют звук как
|
| физический процесс независимо от того, воспринимается звук ухом человека или нет.
|
|
| Уровень интенсивности является объективной и
|
| относительной энергетической характеристикой звука и измеряется в белах или децибелах
|
|
| Уровень громкости — субъективная характеристика звука и
|
| измеряется в фонах.Шкалы фонов и децибел неодинаковы для разных частот и совпадают лишь для частоты 1000 гц
|
|
| Бел (Б) это
|
| единица логарифмической относительной величины (логарифма отношения двух одноименных энергетических физических величин).
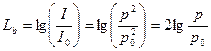 где LB — выраженный в белах уровень интенсивности I и давления р звука относительно Iо и р0, принятого за начальный уровень шкалы
где LB — выраженный в белах уровень интенсивности I и давления р звука относительно Iо и р0, принятого за начальный уровень шкалы
|
|
| Изменение уровня интенсивности на один бел соответствует
|
| Увеличению или уменьшению энергии звука или интенсивности звука в 10 раз, а амплитуда звука меняется в 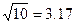 раз раз
|
|
| В качестве эталона тона выбран тон
|
| частотой 1000 Гц
|
|
| Интенсивность эталонного тона на пороге слышимости соответствует
|
| I0=10-12 Вт/м2 или эффективному звуковому давлению Δ р=2. 10-5 Н/м2
|
|
| интенсивность эталонного тона на пороге болевого ощущения соответствует
|
| Iб=10 Вт/м2 или эффективному звуковому давлению Δ р=63 Н/м2
|
|
| Шкала уровней интенсивности звука для эталонного тона составлена следующим образом
|
| Взяли десятичный логарифм отношения интенсивности эталонного тона на пороге болевого ощущения к интенсивности эталонного тона на пороге слышимости и получили 13 Б

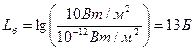 (бел) или (бел) или
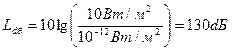 (децибел) (децибел)
|
|
| Изменение уровня интенсивности на 4 Б соответствует
|
| увеличению интенсивности в 104 раз
|
|
| Соответствие между интенсивностью и громкостью звука на разных частотах можно найти
|
| по кривым равной громкости
|
|
| Интенсивность звука, прошедшего через среду, определяется формулой
|
| I=I0e-μ x,
где I — интенсивность звука, прошедшего через среду толщиной x; I0 — интенсивность звука, падающего на среду; μ — постоянная величина (коэффициент поглощения).
|

