СВОЙСТВА ЖИДКОСТЕЙ. ОСОБЕННОСТИ КРОВОТОКА

⇐ ПредыдущаяСтр 5 из 8Следующая ⇒

	ВОПРОС		ОТВЕТ
	На тело, погруженное в жидкость, действует		выталкивающая сила F, равная весу жидкости, вытесненной телом (закон Архимеда): F = pgV, где р — плотность жидкости; g — ускорение силы тяжести; V — объем вытесненной жидкости.
	Коэффициент поверхностного натяжения жидкости α равен		силе поверхностного натяжения F, действующей на единицу длины l контура, ограничивающего поверхность жидкости
	Энергетическое значение коэффициента поверхностного натяжения		равен работе, необходимой для увеличения поверхности жидкости на единицу поверхности, т. е. α есть свободная энергия единицы площади поверхности жидкости:
	Добавочное давление Δ р, вызванное кривизной поверхности жидкости		определяется формулой Лапласа: где R₁ и R₂ — радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости
	Добавочное давление Δ р, вызванное кривизной поверхности жидкости для сферической поверхности (R₁ = R₂ = R)		Δ p=
	Высота поднятия (опускания) жидкости в капилляре		, где θ — краевой угол, R — радиус капилляра, ρ _ж — плотность жидкости, g — ускорение силы тяже.
	Сила трения, действующая на шарик, движущийся внутри вязкой среды, определяется по формуле Стокса:		F = 6 π η Rv, где η — коэффициент внутреннего трения (вязкость); R — радиус шарика; v— скорость движения шарика в жидкости.
	Скорость равномерного падения шарика в вязкой жидкости		, где ρ и ρ _ж — плотности материала, из которого сделан шарик, и жидкости соответственно.
	Сила внутреннего трения, действующая между слоями жидкости площадью S, (уравнение Ньютона)		, где η — вязкость, — градиент скорости.
	Объем жидкости, переносимый за 1 с; через сечение цилиндрической трубы радиусом R (формула Пуазейля)		Q=π R4 через переменное сечение , где L — длина участка трубы, на концах которого поддерживается разность давлений p1-p2
	Гидравлическое сопротивление
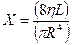
	Рейнольдс доказал, что отсутствие вихрей и подчинение закону Гагена — Пуазейля возможно только в таком потоке		для которого выражение где Re — число Рейнольдса; ρ — плотность; v — скорость жидкости; R — радиус трубки; η — вязкость, не достигает некоторой определенной критической величины; например, для крови Re = 970 ± 80, для воды — в пределах 2000—2400.
	Уравнение неразрывности струи для установившегося (стационарного) движения жидкости выражается формулой		S₁v₁=S₂v₂ где S₁ и S₂ — сечения трубы; v₁ и v₂ — скорости жидкости в соответствующих сечениях.
	Масса жидкости, протекающей ежесекундно через трубу сечением S при установившемся течении со скоростью v, равна		m = ρ Sv, где ρ — плотность жидкости
	запас энергии движущегося потока жидкости определяется		уравнением Бернулли определяет , где pV— потенциальная энергия, обусловленная тем, что жидкость находится под некоторым давлением p; mgh — потенциальная энергия жидкости, поднятой на высоту h относительно земли; mv²/2 кинетическая энергия движущейся жидкости.
	Учитывая, что m/V=ρ, уравнение Бернулли можно записать так		, где р=р_ст статическое давление, ρ gh=р_гидр гидростатическое давление (обусловленное подъёмом жидкости над землей), динамическое давление (обусловленное движением жидкости)
	Для горизонтально расположенных трубок уравнение Бернулли имеет вид		или Для горизонтальной трубки тока гидростатическое давление остается постоянным и может быть отнесено в правую часть
	Уравнение Бернулли формулируется так:		При стационарном течении идеальной жидкости полное давление равное сумме статического, гидростатического и динамического давлений, остается величиной постоянной в любом поперечном сечении потока
	Если в струю жидкости поставить рядом две измерительные трубки: прямую и изогнутую под прямым углом (трубки Пито) то		жидкость в прямой трубке, плоскость отверстия которой расположена параллельно движению жидкости, поднимется на высоту h_c_т относительно свободной поверхности или края потока и определит статическое давление р_ст =ρ gh_c_т, а в изогнутой трубке, плоскость отверстия которой расположена перпендикулярно движению жидкости, поднимется на высоту h_пол относительно свободной поверхности или края потока и определит полное давление р_пол =ρ gh_пол, где ρ плотность движущейся жидкости
	Динамическое давление в потоке жидкости определяется трубками Пито как		разность полного и статического давления т.е. , где ρ плотность движущейся жидкости
	Скорость движения стационарного потока жидкости можно определить трубками Пито		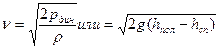, где ρ плотность движущейся жидкости, высота подьёма h_пол в изогнутой трубке и определяющее полное давление, а h_ст высота подьёма в прямой трубке и определяющее статическое давление
	Осмотическое давление недиссоциирующего вещества в растворе равняется		давлению, которое это вещество имело бы в газообразном состоянии в таком же объеме и при той же температуре, как объем и температура данного раствора. На основании этого осмотическое давление р_осм раствора для недиссоциирующих веществ может быть определено из преобразованного уравнения Менделеева — Клапейрона для газов (закон Вант-Гоффа): 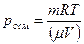, где m— масса вещества, растворенного в объеме V растворителя; μ — молекулярный вес растворенного вещества; R — универсальная газовая постоянная; Т — абсолютная температура раствора.
	Осмотическое давление диссоциирующего вещества в растворе равняется		где α — коэффициент диссоциации; k — число ионов, получающихся при диссоциации одной молекулы.
	Работа левого желудочка сердца равна		, р – среднее давление, V_уд-ударный объём крови в покое, ρ - плотность крови, v_а – скорость кровотока в аорте
	Работа сердца равна		1.2 А_ж, где А_ж – работа левого желудочка сердца
	Скорость распространения пульсовой волны в крупных сосудах		, где ρ — плотность вещества стенки сосуда, r — радиус просвета сосуда, h — толщина стенки сосуда, Е — модуль упругости (модуль Юнга).
	Механическое напряжение стенки кровеносного сосуда		где r — радиус просвета сосуда, h — толщина стенки сосуда.