Анализ стационарного режима автогенератора при фиксированном смещении

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Основной задачей анализа работы АГ является установление связи между токами и напряжениями в его цепях при известных параметрах ГП и КС. Поставленная задача существенно упрощается, если ГП является безынерционным. Ниже будет показано, что именно в этом случае при прочих равных условиях удается реализовать максимальную стабильность частоты генерируемых колебаний. Поэтому будем считать, что .

Зависимости первой гармоники выходного тока ГП от амплитуды высокочастотного напряжения на входном электроде 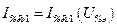носят название колебательных характеристик (рис.4). Для их построения удобно воспользоваться зависимостями 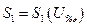рис. 2, умножив каждое значение на соответствующее ему . Для определения точек равновесия целесообразно в поле колебательных характеристик построить линии управляющих сопротивлений в соответствии с соотношением . Точки пересечения колебательных характеристик с линиями управляющего сопротивления, являющиеся точками равновесия «a», «b», «c» и «d» на рис.4 соответствуют одноименным точкам рис. 2. Если учесть, что , условие устойчивости баланса амплитуд в данном случае может быть представлено в виде

. (13)

В соответствии с (13) точка равновесия является устойчивой, если крутизна касательной к колебательной характеристике меньше крутизны линии управляющего сопротивления.

При принудительном изменении смещения точка равновесия будет переходить по линии управляющего сопротивления с одной колебательной характеристики на другую. Естественно, будут изменяться и и . Получающиеся при этом зависимости принято называть диаграммами срыва. На рис. 5 представлены диаграммы срыва, построенные для двух значений . Поясним ход приведенных кривых.

Рис. 4

При (рис. 5, а) колебания в АГ возникают в режиме мягкого самовозбуждения как только превысит 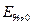. При этом на начальном участке диаграммы в области недонапряженного режима и связаны линейной зависимостью. Таким образом, на начальном участке – прямая линия, наклон которой определяется значением . Ограничение амплитуды колебаний при каждом конкретном значении может осуществляться только за счет уменьшения угла отсечки с ростом , а значения угла отсечки в стационарном режиме лежат в пределах Зависимость рис. 5, б соответствует режиму «жесткого» самовозбуждения.

. При больших значениях , а значит и , ГП переходит в перенапряженный режим и в импульсе выходного тока появляется провал, препятствующий росту его первой гармоники. Поэтому дальнейшее увеличение вызывает лишь незначительное возрастание . Приближенно можно считать, что 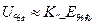, где – напряжение источника питания выходного электрода ГП.

При (рис. 5, б) колебания в АГ возникают также при , но ограничение амплитуды нарастающих колебаний теперь осуществляется только за счет перехода ГП в перенапряженный режим (точка «f» рис. 5, б и 2). Поэтому возрастает скачком до значения, близкого к и при дальнейшем увеличении лишь незначительно изменяется. Если после возникновения колебаний начать принудительное уменьшение , то срыв колебаний наступит при таком смещении , меньшем 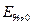, при котором нарушится устойчивость баланса амплитуд, т.е. тогда, когда соответствующая колебательная характеристика станет касательной к линии управляющего сопротивления (точка «e» рис.5, б и 2). Таким образом, на диаграмме срыва появится область гистерезиса, ширина которой будет возрастать с ростом .

Рис. 5

В заключение отметим, что АГ с фиксированным смещением находят весьма ограниченное применение.

Как правило, высокая стабильность амплитуды, а значит и частоты колебаний в АГ обеспечивается при работе ГП в недонапряженном режиме с углом отсечки . Но, как это следует из анализа колебательных характеристик рис.6, точка «1», соответствующая этому случаю, согласно критерию (13) является точкой неустойчивого равновесия, а сам режим возникновения колебаний жестким.

Однако, указанное противоречие удается разрешить при использовании автоматического смещения, например, в АГ на биполярном транзисторе за счет базового и эмиттерного токов (см. рис. 7). Если напряжение источника базового питания больше напряжения запирания , колебания в АГ возникают в режиме мягкого самовозбуждения. увеличение амплитуды колебаний приводит к росту и сопровождается ростом базового и эмиттерного токов, в том числе и их постоянных составляющих и . Это приводит к уменьшению напряжения смещения в соответствии с соотношением

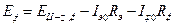
и при определенных значениях и к уменьшению угла отсечки и средней крутизны S₁, что и ограничивает дальнейшее увеличение амплитуды колебаний.

Результирующая колебательная характеристика АГ с автосмещением изображена на рис.6 пунктирной линией. Нетрудно убедиться, что в соответствии с (13) для этой колебательной характеристики точка равновесия «1» является устойчивой.

Подчеркнем, что для получения подобной характеристики необходимо, чтобы напряжение успевало следить за изменением амплитуды колебаний. Для этого постоянные времени цепей автоматического смещения и должны быть меньше постоянной времени колебательной системы , где 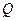– нагруженная добротность колебательной системы; – частота генерируемых колебаний.

Рис. 6 Рис. 7

Если цепочка автоматического смещения обладает большой постоянной времени, АГ переходит в режим прерывистой генерации. В этом случае при возникновении колебаний их амплитуда быстро нарастает до значения . Затем начинается заряд конденсаторов цепей автоматического смещения и постепенное уменьшение и до тех пор, пока напряжение смещения между базой и эмиттером не достигнет значения , при котором наступает срыв колебаний. После того, как колебания прекращаются, начинается разряд конденсаторов 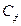и и напряжение постепенно возрастает. При достижении смещением значения , колебания АГ возникают вновь и процесс повторяется. На рис.6 показано перемещение рабочей точки АГ на семействе колебательных характеристик при прерывистой генерации. В приведенном на данном рисунке примере = 0, а = .

Схемы автогенераторов

При синтезе схем одноконтурных АГ первоначально рассмотрим случай, когда среднюю крутизну ГП можно считать вещественной величиной. Это позволяет представить уравнение стационарного состояния в виде (7). Далее допустим, что, как и ранее, добротность КС достаточно велика. Следовательно, остается справедливым выражение (10). Поскольку для выполнения условия равновесия должно быть вещественным и положительным из (10) следует, что

, (14)
а двухполюсники и должны быть одного знака, т.е. либо оба быть катушками индуктивности, либо конденсаторами. Знак реактивного сопротивления двухполюсника должен быть противоположным, что вытекает непосредственно из уравнения (14). Сказанное позволяет построить две возможные схемы АГ, представленные на рис.8 и предполагающие, что в качестве ГП использован биполярный транзистор.

Рис. 8

Схема рис.8, а носит название емкостной трехточки и в ней ; ; . В схеме рис.8, б ; ; и она называется индуктивной трехточкой.

Рис. 9

Из соотношения (14) также следует, что при принятых допущениях частота генерируемых колебаний равна собственной резонансной частоте КС. Тогда , а коэффициент обратной связи в любой их схем рис.8 с учетом (14) определяется соотношением

Помимо рассмотренных, к простейшим относится и трансформаторная схема, представленная на рис. 8, в. В этой схеме противофазность напряжений на входном и выходном электродах ГП обеспечивается соответствующим включением обмоток трансформатора.

На рис. 9 представлена принципиальная схема АГ, выполненного по классической схеме емкостной трехточки. В АГ использовано параллельное питание коллекторной цепи. Номиналы блокировочных и разделительных элементов в коллекторной и базовой цепях выбираются из тех же требований, что и в случае ГВВ. В базовой цепи используется автоматическое смещение, особенности осуществления которого были рассмотрены выше. Подчеркнем, что наличие резистора позволяет также стабилизировать режим работы транзистора при изменении температуры окружающей среды и напряжения источника питания.

Сравнительный анализ простейших схем АГ показывает, что лучшими характеристиками с точки зрения стабильности частоты обладает емкостная трехточечная схема, что и определяет ее широкое использование при создании автогенераторов.

Как уже отмечалось, воздействие внешних дестабилизирующих факторов, воздействующих на параметры КС и ГП, приводит к изменению одного или нескольких фазовых углов, входящих в уравнение баланса фаз, что сопровождается изменением частоты генерируемых колебаний

При определении изменения частоты колебаний АГ под воздействием различных дестабилизирующих факторов, можно воспользоваться соотношением:

, (15)
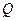где , и - малые приращения , и соответственно, вызванные действием дестабилизирующих факторов.

Анализ полученного выражения показывает, что с увеличением 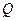и уменьшением уменьшается влияние относительного изменения фазового угла средней крутизны и добротности колебательной системы на частоту генерируемых колебаний. Причина отмеченного явления заключается в том, что с ростом 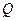увеличивается крутизна фазовой характеристик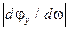и при и, в соответствии с комментариями к (9), уменьшается приращение , обусловленное изменением фазовых углов. Аналогичным образом можно пояснить и уменьшение чувствительности к изменению при уменьшении абсолютного значения фазового угла средней крутизны, поскольку при этом стремится к и 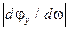возрастает. Что же касается отклонения частоты от номинального значения, обусловленного изменением собственной резонансной частоты КС, то оно, как это следует из (15), практически не зависит от значения и и с достаточной точностью можно считать, что . Само изменение резонансной частоты обусловлено изменением и 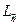и в первом приближении равно

Таким образом, обеспечение высокой стабильности частоты, т. е. незначительного изменения при изменении внешних воздействий требует в первую очередь малой чувствительности к изменению параметров ГП и КС. Поэтому при построении высокостабильных АГ следует использовать усилительные элементы, в которых на частоте генерации еще не проявляются инерционные свойства, и колебательные системы с высокой добротностью и эталонностью. Под эталонностью понимается способность КС поддерживать постоянство собственной резонансной частоты при изменении тех или иных внешних условий.

Кварцевые автогенераторы

Описанные выше АГ с КС на L, C элементах обладают относительно низкой стабильностью частоты ( ). В тех случаях, когда требуется более высокая стабильность частоты, в автогенераторах применяются механические колебательные системы, из которых наиболее широкое распространение получили кварцевые резонаторы (КвР).

Существование прямого и обратного пьезоэлектрического эффекта в кварце, допускающего практически полное преобразование электрической энергии в механическую и обратно, делает удобным использование КвР в качестве колебательной системы автогенератора.

КвР, имеющие обычно форму пластин, стержней или чечевиц, вырезают из кристалла кварца, ориентируя определенным образом оси симметрии резонаторов относительно кристаллографических осей. Это позволяет получить резонаторы с заданными физическими свойствами и в первую очередь с требуемым значением температурного коэффициента частоты.

В КвР может быть возбуждено несколько видов механических колебаний. Наибольшее распространение в последнее время получили колебания сжатия и растяжения по длине и ширине, сдвига по толщине и в меньшей степени по ширине; изгиба по ширине и толщине и крутильные колебания по длине.

Частота собственных колебаний определяется скоростью распространения упругих волн и протяженностью их пути, т.е. расстоянием между гранями отражения : . Как во всякой колебательной системе с распределенными параметрами, в КвР наблюдается ряд частот колебаний данного вида, число которых в общем случае бесконечно. Колебания более высоких частот этого ряда называются обертонами (модами). Обертоны, частоты которых находятся в почти кратных отношениях с частотой низшего колебания, иногда называют механическими гармониками. Поскольку скорости распространения упругих волн для разных видов колебаний различны для расширения возможного диапазона частот кварцевых резонаторов используют различные виды колебаний, а в пределах одного вида – разные срезы, колебания на обертонах, распространение упругих волн в направлении различных размеров и, наконец, варьируют размеры самого резонатора. При этом диапазон рабочих частот КвР простирается от сотен герц до сотен мегагерц.

Простейший КвР по своему устройству подобен плоскому конденсатору, помещенному в вакуумированный или герметизированный корпус и состоящему из кварцевой пластины, противоположные грани которой покрыты слоем металлизации, и кварцедержателя, служащего для крепления кварцевой пластины и осуществляющего электрический контакт с металлизированной поверхностью, но не препятствующего механическим колебаниям резонатора.

Рис. 10

Эквивалентная электрическая схема КвР рис. 10 может быть представлена в виде параллельного соединения емкости кварцедержателя C₀ и, в общем случае, бесконечного числа , , контуров, резонансные частоты которых совпадают с частотами механических колебаний кварцевой пластины. Однако, поскольку КвР является высокодобротной колебательной системой, при построении эквивалентной схемы, справедливой для узкого диапазона, вблизи каждой из частот гармоник, влиянием всех последовательных контуров, кроме одного, настроенного на эту частоту, можно пренебречь.

К основным параметрам эквивалентной схемы КвР относятся динамические индуктивность 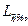и емкость , емкость кварцедержателя , сопротивление потерь , добротность резонатора и коэффициент включения .

Номиналы элементов эквивалентной схемы резонатора существенно отличаются от соответствующих элементов обычных колебательных контуров. Так Гн; пФ; пФ; Ом; . Недостижимое в обычных , контурах такое значение добротности является одной из причин высокой стабильности частоты АГ с кварцевыми резонаторами.

Эквивалентная схема КвР характеризуется двумя резонансными частотами: частотой последовательного резонанса в динамической ветви

и частотой параллельного резонанса

Коэффициент включения существенно меньше единицы ( ), поэтому изменение параметров внешних по отношению к резонатору элементов, подключаемых параллельно емкости , практически не влияет на значение . При рассмотрении эквивалентного сопротивления резонатора его удобно представить в виде последовательного соединения резистивного и реактивного двухполюсников .

На рис.11 приведены частотные характеристики ; ; и , вычисленные для резонатора со следующими параметрами: МГц; пФ; пФ; Ом; (сплошные линии) и (пунктирные линии). Внутри резонансного промежутка эквивалентное сопротивление КвР носит индуктивный характер, а вне его – емкостной. При частоты и сливаются, а при участок, на котором наблюдается индуктивное сопротивление КвР, вообще отсутствует. Фазочастотная характеристика резонатора имеет наибольшую крутизну в узких диапазонах частот и , где .

Рис. 11

Высокое значение крутизны фазочастотной характеристики КвР является основной причиной, обеспечивающей высокую стабильность частоты кварцевых АГ. Широко используемые на практике схемы автогенераторов с кварцевой стабилизацией, несмотря на их многообразие, можно разбить на две большие группы. К первой группе схем относятся те, в которых КвР включается вместо одного из двухполюсников , или в обобщенной трехточечной схеме АГ рис.12.

Рис. 12

Это так называемые осцилляторные схемы. В них эквивалентное сопротивление КвР должно носить индуктивный характер, а выход резонатора из строя приводит к срыву колебаний, поскольку невозбужденный КвР имеет емкостной характер эквивалентного сопротивления. В осцилляторных схемах частота генерации 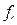удовлетворяет условию . Во вторую группу схем можно включить схемы с КвР в цепи обратной связи и схемы с КвР в контуре. Во всех этих схемах, как правило, помимо КвР имеется обычный колебательный контур, обеспечивающий выполнение условий самовозбуждения. Отличительной особенностью схем второй группы является возможность сохранения колебаний в автогенераторе при закорачивании КвР, поскольку в них используется последовательный резонанс кварца. Схемы с кварцем в цепи обратной связи могут быть получены из схемы рис.12 путем включения КвР в одну из ветвей, соединяющих колебательный контур с эмиттером или базой транзистора, а схемы с кварцем в контуре – включением КвР последовательно с одним из двухполюсников , или . В обеих схемах генерация происходить на частотах, близких к частоте . Возможные осцилляторные схемы кварцевых АГ представлены на рис.13, - а, б и в. Схема рис. 13, а при индуктивном характере эквивалентного сопротивления резонатора сводится к емкостной трехточечной схеме, а схемы рис. 13, б и в – к индуктивной. Из этих схем наибольшее применение на практике находит схема с КвР между коллектором и базой транзистора, обеспечивающая наибольшую стабильность частоты. Последнее обусловлено меньшим шунтированием кварцевого резонатора самим транзистором, малым влиянием собственных емкостей транзистора на резонансную частоту КС и тем, что высшие гармоники в базовом и коллекторном напряжениях ослаблены емкостями и .

Рис.13

Основные особенности процессов, происходящих в осцилляторных схемах, рассмотрим на примере схемы АГ рис. 13, а. Пренебрегая, как и ранее, фазовым углом средней крутизны, для определения частоты генерации можно воспользоваться соотношением (14), которое в данном случае приобретает вид

. (16)

Рис. 14

Графическое решение (16) представлено на рис. 14. Из двух возможных значений частоты генерации и 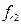следует выбрать меньшую, поскольку только при выполняется условие устойчивости баланса фаз (12).

При построении АГ, работающих на частотах, превышающих 10 МГц, обычно используют КвР с колебаниями на высших механических гармониках. Для исключения возможности генерации на частотах гармоник, отличных от заданной, схему генератора рис. 13, а приходится усложнять, включая, например, между базой и эмиттером транзистора последовательный , контур, а между эмиттером и коллектором – параллельный ( , ). Нетрудно убедиться, что, если резонансные частоты каждого из контуров удовлетворяют неравенствам

, ,

(здесь 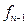, и – частоты гармоник с номерами ( ), и ( ), соответственно), баланс фаз в АГ будет выполняться только вблизи частоты n-ой гармоники.

Используя работу КвР на -ой механической гармонике, необходимо также учитывать, что емкость в динамической ветви уменьшится в раз по сравнению с ее значением на основной частоте. Это может нарушить неравенство , необходимое для реализации осцилляторных схем. В подобных случаях требуется нейтрализовать емкость кварцедержателя . Наиболее просто это можно осуществить, подключая параллельно КвР катушку индуктивности , образующую с емкостью параллельный контур, настроенный на частоту генерации.

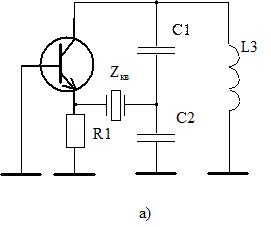
Рис.15

Однако наиболее часто при построении АГ, работающих на частотах высших механических гармоник КвР, находят применение фильтровые схемы и в первую очередь схемы с КвР в цепи обратной связи. Принцип работы таких схем основан на том, что сопротивление кварцевого резонатора минимально вблизи частоты последовательного резонанса и резко возрастает при удалении от нее. Следовательно, условия самовозбуждения, выполняемые вблизи частоты , будут нарушаться на всех других частотах. Отсутствие генерации на отличных от требуемой гармониках обеспечивается собственной колебательной системой АГ. Для реализации высокой фиксирующей способности КвР, а следовательно, и высокой стабильности частоты генерируемых колебаний 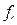необходимо, чтобы в цепи обратной связи последовательно с КвР не включались элементы, сопротивление которых на частоте было бы сравнимо или больше . С этой точки зрения более предпочтительной оказывается схема, представленная на рис.15, а, в которой база транзистора заземлена, а КвР включен в цепь, связывающую эмиттер с колебательной системой. Аналогичный результат можно получить и используя схему рис.15, б, в которой для получения низкого входного сопротивления транзистора в точке подключения КвР используется балластный резистор .

Угловая модуляция

Во многих случаях, например при угловой модуляции, полная фаза формируемого сигнала должна изменяться по закону, определяемому модулирующим напряжением. Полная фаза и частота колебаний связаны друг с другом известными соотношениями:

= и (17)

Различают два вида угловой модуляции: частотную (ЧМ) и фазовую (ФМ). При ЧМ пропорциональным модулирующему сигналу является изменение частоты , а при ФМ – изменение полной фазы несущего колебания , т.е. = а при ЧМ и = b при ФМ, где а и b – коэффициенты пропорциональности. При использовании гармонического модулирующего сигнала = с учетом (18) получим:

для ЧМ = =

= = (18)

для ФМ = =

= , (19)

где и 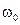– амплитуда и частота несущего колебания. В качестве характеристик ЧМ- и ФМ- колебаний используют девиацию частоты – максимальное отклонение частоты от своего среднего значения и индекс модуляции – максимальное отклонение фазы колебаний. Из соотношений (18) и (19) следует, что:

при ЧМ = ; = / ; = ;

при ФМ = ; = ; = ,

т.е. при обоих видах угловой модуляции девиация частоты и индекс модуляции пропорциональны модулирующему напряжению. Зависимость же этих параметров от частоты модулирующего сигнала различна: при ЧМ девиация частоты не зависит от частоты , а индекс модуляции обратно пропорционален частоте; при ФМ девиация частоты прямо пропорциональна , а индекс модуляции не зависит от .

Рассматриваемые виды угловой модуляции могут быть преобразованы из одного в другой путем обработки модулирующего сигнала в блоке с частотно-зависимым коэффициентом передачи.

Колебание с угловой модуляцией гармоническим сигналом может быть представлено следующим образом:

, (20)
где 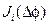– функция Бесселя 1-го рода i-го порядка от аргумента . Отсюда следует, что спектр такого сигнала состоит бесконечного числа составляющих, частоты которых отличаются на .

Если индекс модуляции , то , , а (при n > 1). Тогда, как следует из (20), спектр колебания содержит всего три составляющие ( 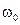, и ) и от спектра амплитудно-модулированного сигнала отличается только фазой составляющей разностной частоты. Угловая модуляция с таким спектром носит название узкополосной, а мощности отдельных спектральных составляющих такие же, как и амплитудной с глубиной модуляции .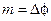

В общем случае спектр сигнала с широкополосной угловой модуляцией бесконечен, однако на практике в полосу сигнала включают только спектральные компоненты, амплитуда которых составляет не менее 10 – 15 % амплитуды несущего немодулированного колебания. При этом их число , а занимаемую сигн

⇐ Предыдущая 1 234 5 Следующая ⇒