Алгоритм нахождения решения по методу Гаусса

⇐ ПредыдущаяСтр 2 из 2

1) Полагая, что в расширенной матрице системы коэффициент (если это не так, то следует на первое место поставить строку с отличным от нуля коэффициентом при ), преобразуем матрицу следующим образом: первую строку оставляем без изменения, а из всех остальных строк исключаем неизвестную с помощью эквивалентных преобразований.

2) В полученной матрице, считая, что (что всегда можно получить, переставив строки), оставляем без изменений первые две строки, а из остальных строк расширенной матрицы, используя вторую строку, с помощью элементарных преобразований исключаем неизвестную .

3) Во вновь полученной матрице, при условии оставляем без изменений первые три строки, а из всех остальных с помощью третьей строки элементарными преобразованиями исключаем неизвестную .

Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:

1) если в результате приходим к ступенчатой матрице соответствующей системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;

2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;

3) если получается система с трапецеидальной матрицей коэффициентов и при этом не выполняется условие пункта 1), то система совместна и неопределенна.

Если матрицу размера можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера и стоящую справа прямоугольную матрицу, то матрицу назовем трапециевидной или трапецеидальной.

Матрица – трапециевидная матрица.

Методика и порядок выполнения работы

Пример 1

Решить систему уравнений методом Гаусса:

Решение

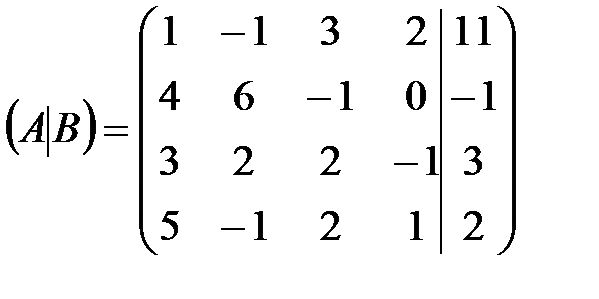
Для исходной системы уравнений запишем расширенную матрицу и приведем ее к ступенчатому виду с помощью элементарных преобразований:

Проведенные элементарные преобразования:

1) поскольку в первой матрице элемент , то первую строку оставим без изменений;

2) вместо второй строки запишем ее сумму с первой, умноженной на (-4);

3) вместо третьей строки запишем ее сумму с первой строкой, умноженной на (-3);

4) вместо четвертой строки запишем ее сумму с первой строкой, умноженной на (-5).

Полученная новая матрица эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при (это и являлось целью преобразований 1 – 4).

Преобразуем полученную матрицу следующим образом:

1) первые две строки оставим без изменения, поскольку элемент ;

2) вместо третьей строки запишем сумму второй строкой и третьей, умноженной на (-2);

3) четвертую строку заменим суммой удвоенной второй строкой и умноженной на (-5) четвертой.

В результате получится матрица, соответствующая системе, у которой неизвестное исключено из всех уравнений, кроме первого, а неизвестное – из всех уравнений кроме первого и второго:

Далее исключаем неизвестную из четвертого уравнения. Для этого последнюю матрицу преобразуем так:

1) первые три строки оставим без изменения, так как ;

2) четвертую строку заменим суммой третьей, умноженной на (-39), и четвертой.

Полученная ступенчатая матрица соответствует системе уравнений:

Из последнего уравнения этой системы получаем . Подставив это значение в третье уравнение, получим . Из второго уравнения следует, что , а из первого – . Очевидно, что полученное решение единственно (так как единственным образом определяется значение , затем и т. д.).

Пример 2

Решить систему уравнений методом Гаусса:

Решение

Проведенные элементарные преобразования:

1) первую строку оставим без изменения;

2) вместо второй строки запишем сумму второй строкой и первой, умноженной на (-2);

3) вместо третьей строки запишем сумму третьей строкой и первой, умноженной на (-3);

4) четвертую строку заменим суммой четвертой и первой, умноженной на (-1);

5) пятую строку заменим суммой пятой строки и первой, умноженной на (-2).

В результате преобразований получили матрицу эквивалентную данной. Оставив без изменения первые две строки этой матрицы, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки приведем к нулю коэффициенты при в четвертой и пятой строках. После деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получили матрицу ступенчатого вида, каждая из двух последних строк которой соответствует уравнению . Это уравнение удовлетворяется любым набором чисел , , , и и его следует удалить из системы.

Для последней матрицы составляем соответствующую систему:

В качестве базисных (главных) переменных можно выбрать , и , соответствующие столбцам минора третьего порядка , тогда и – свободные переменные. Придавая свободным переменным произвольные значения , а , из последнего уравнения системы получим: . Подставив выражения , и во второе уравнение той же системы, получим . Теперь из первого уравнения можно получить . Окончательно решение системы представляется в виде:

Пример 3

Решить систему методом Крамера:

Решение

1) Вычислим определитель системы:

Так как определитель системы , то система совместна и определена. Причем решения системы можно найти по формулам Крамера.

2) Вычислим определители и :

3) Находим решения:

Таким образом, , .

Пример 4

Решить систему с помощью матричного исчисления:

Решение

1) Найдем определитель матрицы :

Так как определитель , то матрица – невырожденная и для нее существует обратная матрица.

2) Определим алгебраические дополнения ко всем элементам матрицы.

3) Составим присоединенную матрицу :

4) Вычислим обратную матрицу:

5) Найдем решение системы:

Итак, , , .

Задания

Задание 1

Проверить совместность системы уравнений и в случае совместности решить ее двумя способами: 1) по формулам Крамера, 2) методом Гаусса.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Задание 2

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

Задание 3

Найти общее и одно частное решения системы линейных уравнений методом Гаусса.

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

3.9.

3.10.

Задание 4

Дана система линейных уравнений. Доказать её совместность и решить двумя способами: 1) методом Крамера; 2) средствами матричного исчисления.

4.1. 4.2.

4.3. 4.4.

4.5. 4.6.

4.7. 4.8.

4.9. 4.10.

Содержание отчета и его форма

Выбрать вариант своего задания. Номер варианта соответствует номеру, под которым записана фамилия студента в журнале группы. Отчет о выполнении лабораторной работы необходимо оформлять по предложенному выше образцу.

При выполнении лабораторной работы необходимо придерживаться указанных выше правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

Вопросы для защиты работы

1. Что называется решением системы?

2. Какая классификация систем в зависимости от существования решения вам известна?

3. Какие системы называются равносильными?

4. Какие преобразования считаются элементарными?

5. Метод Крамера.

6. Матричный метод решения СЛАУ.

7. Метод Гаусса.

8. Может ли частное решение системы линейных уравнений совпадать с ее общим решением?

9. Могут ли различные методы решения системы линейных уравнений (метод Крамера, метод Гаусса и метод обратной матрицы) дать различные ответы?

10. Возможно ли, чтобы система линейных уравнений имела решение с помощью метода Гаусса, но не имела решения по формулам Крамера?

Список основной литературы

1. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: Учеб. Пособие для студентов втузов. В 2-х ч. Ч. Ι. – М.: Высш. Шк., 1986.

2. Линейная алгебра: Учебное пособие / Под ред. В. С. Зарубина, А. Л. Криценко. Вып. IV. М.: Изд-во МГТУ, 2001.

⇐ Предыдущая 12