Системы линейных алгебраических уравнений

Лабораторная работа 1

Тема: Решение СЛАУ по формулам Крамера и методом Гаусса.

Цель: оказание студентам помощи в овладении навыками решения задач, отражающих тематику данной лабораторной работы; научить студентов решать СЛАУ.

Теоретическое обоснование

Системы линейных алгебраических уравнений

Система линейных уравнений с переменными имеет вид:

(1)

где ( ) – произвольные числа называющиеся коэффициентами при переменных, а – свободными членами уравнений.

Система (1) называется однородной, если все её свободные члены равны нулю, если хотя бы одно из чисел отлично от нуля, то система называется неоднородной.

Решением системы называется такая совокупность чисел , , …, , при подстановке которых данное уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если решений нет.

Совместная система называется определённой, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, умножение обеих частей какого-либо уравнения системы на отличное от нуля число. С помощью элементарных преобразований системы уравнений получается система равносильная данной.

Теорема (Кронекера - Капелли):

Для того чтобы система (1) линейных алгебраических уравнений относительно неизвестных была совместна (имела решение), необходимо и достаточно, чтобы ранг основной матрицы (А) системы и ранг

расширенной матрицы (А, В) системы (1) были равны, т. е. .

Рангом матрицы (обозначается или ) называется наибольший порядок порожденных ею определителей, отличных от нуля.

Методы решения СЛАУ

1. Матричный метод.

Пусть дана система уравнений (1) записанная в виде матричного уравнения

(2)

Если основная матрица невырожденная, т.е. , тогда для матрицы существует обратная матрица . Умножив матричное уравнение (2) слева на , получим:

Откуда

(3)

Следовательно, (3) – матричное решение уравнения (2).

Обратная матрица для матрицы определяется по формуле:

или

где – определитель матрицы ; – присоединенная матрица, составленная из алгебраических дополнений; – алгебраические дополнения элементов матрицы .

2. Метод Крамера.

Рассмотрим систему из уравнений с неизвестными:

(4)

Определитель -го порядка , составленный из коэффициентов при неизвестных, называется определителем системы. В зависимости от определителя различают следующие случаи:

1) если определитель системы отличен от нуля, то система имеет единственное решение, которое может быть определено по формулам Крамера

, , …, ,

где определитель -го порядка ( ) получается из путем замены -го столбца свободными членами , , …, .

2) Если , но хотя бы один из ( ), то система несовместна.

3) Если и ( ), то система либо несовместна, либо имеет бесчисленное множество решений.

3. Метод Гаусса.

Эффективным методом решения и исследования систем линейных уравнений является метод исключения неизвестных, называемый методом Гаусса. Преобразование системы по методу Гаусса состоит из нескольких шагов, на каждом из которых производится исключение одного неизвестного. Для каждого такого шага необходимо указать ведущее неизвестное и ведущее уравнение, а также определить из каких уравнений исключается ведущее неизвестное.

В качестве первого ведущего элемента (ведущего элемента 1-го шага можно выбрать любой отличный от нуля коэффициент данной системы уравнений). Произведя такой выбор, исключим 1-ое ведущее неизвестное из всех уравнений системы, используя элементарные преобразования:

1) прибавление к обеим частям одного уравнения системы соответствующих частей другого уравнения той же системы, умноженных на некоторое число;

2) перестановка местами уравнений в системе;

3) удаление из системы уравнений вида 0=0.

Совокупность уравнений системы, кроме 1-го ведущего, назовём первой подсистемой. Первое ведущее уравнение дальнейшим преобразованиям подвергать не будем. В качестве второго ведущего элемента (ведущего элемента 2-го шага) можем выбрать любой отличный от нуля коэффициент в 1-ой подсистеме. Произведя такой выбор, исключим 2-ое ведущее неизвестное из всех уравнений 1-ой подсистемы, кроме 2-го ведущего.

Совокупность уравнений системы, кроме 1-го и 2-го ведущих, назовём 2-ой подсистемой. Второе ведущее уравнение также как и 1-ое, дальнейшим преобразованиям подвергать не будем.

В качестве третьего ведущего элемента (ведущего элемента 3-го шага) можно выбрать любой отличный от нуля коэффициент во 2-ой подсистеме и т.д.

Если в процессе хотя бы одно уравнение вида (5) ( ), то исследование закончено – система несовместна. Если же появится уравнение вида (6), то его просто удалим. Если в процессе не появятся уравнения (5) и (6), то данная система совместна.

Процесс её преобразования закончится тогда, когда на очередном шаге мы получим подсистему, состоящую только из 1-го уравнения, или подсистема вообще не будет иметь вид (7).

На каждом шаге преобразования системы линейных, уравнений по методу Гаусса мы имеем большую свободу в выборе ведущего элемента (он не может только равняться нулю). Но как бы мы эти элементы не выбирали, число уравнений в окончательно полученной системе будет одним и тем же, оно равно максимальному числу независимых уравнений в исходной системе это число и является рангом системы ( ).

Приведение системы к виду (7) называется прямым ходом, отыскание решения системы (7) – обратным ходом метода Гаусса.

(7)

или

В случае система имеет единственное решение, которое легко найти. Если же , то из системы (7) находим значения неизвестных , , …, через неизвестные , …, .

Придавая неизвестным , …, произвольные значения будем получать решение системы.

При этом неизвестные , …, называют свободными, а неизвестные , , …, – базисными. Число базисных неизвестных равно рангу системы , а число свободных неизвестных ( – число неизвестных).

Базисные неизвестные единственным образом выражаются через свободные неизвестные.

Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением.

Если свободные неизвестные выражены через параметры, то получается решение, которое называется общим решением.

Все бесконечное множество решений системы можно получить, придавая свободным неизвестным любые числовые значения и находя соответствующие значения базисных неизвестных.

Если всем свободным неизвестным приданы нулевые значения, то полученное решение называется базисным.

Метод Гаусса – матричный способ.

Оформляют решение по методу Гаусса так: записывают расширенную матрицу системы. Затем над строками производят элементарные преобразования, приводя данную матрицу к диагональному виду.

Пример 1

Решить систему уравнений методом Гаусса:

Решение

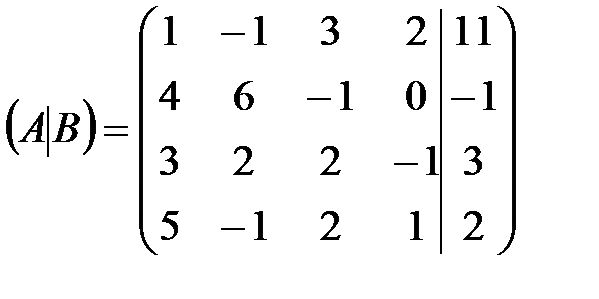
Для исходной системы уравнений запишем расширенную матрицу и приведем ее к ступенчатому виду с помощью элементарных преобразований:

Проведенные элементарные преобразования:

1) поскольку в первой матрице элемент , то первую строку оставим без изменений;

2) вместо второй строки запишем ее сумму с первой, умноженной на (-4);

3) вместо третьей строки запишем ее сумму с первой строкой, умноженной на (-3);

4) вместо четвертой строки запишем ее сумму с первой строкой, умноженной на (-5).

Полученная новая матрица эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при (это и являлось целью преобразований 1 – 4).

Преобразуем полученную матрицу следующим образом:

1) первые две строки оставим без изменения, поскольку элемент ;

2) вместо третьей строки запишем сумму второй строкой и третьей, умноженной на (-2);

3) четвертую строку заменим суммой удвоенной второй строкой и умноженной на (-5) четвертой.

В результате получится матрица, соответствующая системе, у которой неизвестное исключено из всех уравнений, кроме первого, а неизвестное – из всех уравнений кроме первого и второго:

Далее исключаем неизвестную из четвертого уравнения. Для этого последнюю матрицу преобразуем так:

1) первые три строки оставим без изменения, так как ;

2) четвертую строку заменим суммой третьей, умноженной на (-39), и четвертой.

Полученная ступенчатая матрица соответствует системе уравнений:

Из последнего уравнения этой системы получаем . Подставив это значение в третье уравнение, получим . Из второго уравнения следует, что , а из первого – . Очевидно, что полученное решение единственно (так как единственным образом определяется значение , затем и т. д.).

Пример 2

Решить систему уравнений методом Гаусса:

Решение

Проведенные элементарные преобразования:

1) первую строку оставим без изменения;

2) вместо второй строки запишем сумму второй строкой и первой, умноженной на (-2);

3) вместо третьей строки запишем сумму третьей строкой и первой, умноженной на (-3);

4) четвертую строку заменим суммой четвертой и первой, умноженной на (-1);

5) пятую строку заменим суммой пятой строки и первой, умноженной на (-2).

В результате преобразований получили матрицу эквивалентную данной. Оставив без изменения первые две строки этой матрицы, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки приведем к нулю коэффициенты при в четвертой и пятой строках. После деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получили матрицу ступенчатого вида, каждая из двух последних строк которой соответствует уравнению . Это уравнение удовлетворяется любым набором чисел , , , и и его следует удалить из системы.

Для последней матрицы составляем соответствующую систему:

В качестве базисных (главных) переменных можно выбрать , и , соответствующие столбцам минора третьего порядка , тогда и – свободные переменные. Придавая свободным переменным произвольные значения , а , из последнего уравнения системы получим: . Подставив выражения , и во второе уравнение той же системы, получим . Теперь из первого уравнения можно получить . Окончательно решение системы представляется в виде:

Пример 3

Решить систему методом Крамера:

Решение

1) Вычислим определитель системы:

Так как определитель системы , то система совместна и определена. Причем решения системы можно найти по формулам Крамера.

2) Вычислим определители и :

3) Находим решения:

Таким образом, , .

Пример 4

Решить систему с помощью матричного исчисления:

Решение

1) Найдем определитель матрицы :

Так как определитель , то матрица – невырожденная и для нее существует обратная матрица.

2) Определим алгебраические дополнения ко всем элементам матрицы.

3) Составим присоединенную матрицу :

4) Вычислим обратную матрицу:

5) Найдем решение системы:

Итак, , , .

Задания

Задание 1

Проверить совместность системы уравнений и в случае совместности решить ее двумя способами: 1) по формулам Крамера, 2) методом Гаусса.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Задание 2

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

Задание 3

Найти общее и одно частное решения системы линейных уравнений методом Гаусса.

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

3.9.

3.10.

Задание 4

Дана система линейных уравнений. Доказать её совместность и решить двумя способами: 1) методом Крамера; 2) средствами матричного исчисления.

4.1. 4.2.

4.3. 4.4.

4.5. 4.6.

4.7. 4.8.

4.9. 4.10.

Содержание отчета и его форма

Выбрать вариант своего задания. Номер варианта соответствует номеру, под которым записана фамилия студента в журнале группы. Отчет о выполнении лабораторной работы необходимо оформлять по предложенному выше образцу.

При выполнении лабораторной работы необходимо придерживаться указанных выше правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

Вопросы для защиты работы

1. Что называется решением системы?

2. Какая классификация систем в зависимости от существования решения вам известна?

3. Какие системы называются равносильными?

4. Какие преобразования считаются элементарными?

5. Метод Крамера.

6. Матричный метод решения СЛАУ.

7. Метод Гаусса.

8. Может ли частное решение системы линейных уравнений совпадать с ее общим решением?

9. Могут ли различные методы решения системы линейных уравнений (метод Крамера, метод Гаусса и метод обратной матрицы) дать различные ответы?

10. Возможно ли, чтобы система линейных уравнений имела решение с помощью метода Гаусса, но не имела решения по формулам Крамера?

Список основной литературы

1. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: Учеб. Пособие для студентов втузов. В 2-х ч. Ч. Ι. – М.: Высш. Шк., 1986.

2. Линейная алгебра: Учебное пособие / Под ред. В. С. Зарубина, А. Л. Криценко. Вып. IV. М.: Изд-во МГТУ, 2001.

Лабораторная работа 2

Тема: Линейные системы. Фундаментальная система решений. Применения теоремы Кронекера-Капелли.

Цель: оказание студентам помощи в овладении навыками решения задач, отражающих тематику данной лабораторной работы; научить студентов исследовать СЛАУ, применяя теорему Кронекера-Капелли, и находить фундаментальную систему решения.

Теоретическое обоснование

Задания

Задание 1. Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Задание 2. Найти фундаментальныйнабор решений однородной системы линейных уравнений.

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

Задание 3. Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

3.9.

3.10.

Пример 1

Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.

Решение

× (-4) × (-7)

С помощью элементарных преобразований приведем матрицу системы к ступенчатому виду:

Из последней ступенчатой системы видно, что ранг матрицы системы равен , а количество переменных равно , так как , то система неопределенна.

Количество базисных переменных равно . В качестве главных переменных можно выбрать и , соответствующие столбцам ненулевого минора второго порядка: , в качестве свободной переменной – .

Запишем систему, соответствующую полученной матрице:

Из второго уравнения выражаем через , получим: . Подставляя это выражение в первое уравнение, получим: . Обозначив , получим общее решение системы . это решение можно записать в виде: . Фундаментальную систему решений образует решение .

Пример 2

Найти фундаментальныйнабор решений однородной системы линейных уравнений.

Решение

× (-3) × (-4) × (-3)

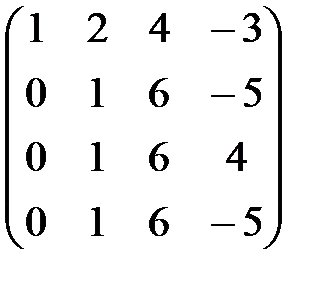С помощью элементарных преобразований приведем матрицу системы к ступенчатому виду:

× (-1) × (-1/3) × (1/2)

× (-1) × (-1)

Количество базисных переменных равно . В качестве главных переменных можно выбрать , и , соответствующие столбцам ненулевого минора третьего порядка: , в качестве свободной переменной – .

Запишем систему, соответствующую полученной матрице:

Из третьего уравнения получим: . Подставляя это выражение в первое и второе уравнения, получим: , . Обозначив , получим общее решение системы . это решение можно записать в виде: . Фундаментальную систему решений образует решение .

Пример 3

Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.

Решение

Проведем элементарные преобразование расширенной матрицы системы по методу Гаусса:

× (-2) × (-2) × (-3)

× 1 × (-1)

~ .

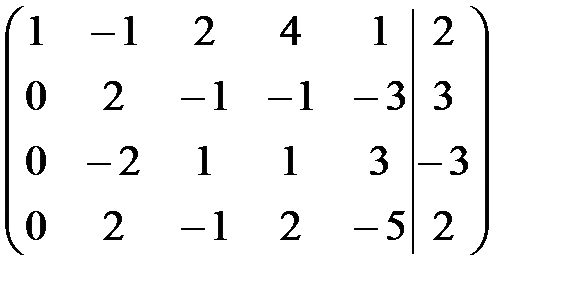Из последней ступенчатой системы видно, что ранг матрицы системы равен , ранг расширенной матрицы равен , а количество переменных равно , так как , то система совместна и неопределенна.

Количество базисных переменных равно . В качестве главных переменных можно выбрать , и , соответствующие столбцам ненулевого минора третьего порядка: , в качестве свободных переменных – и .

Запишем систему, соответствующую полученной матрице:

Из третьего уравнения выражаем через , получим: . Подставляя это выражение во второе уравнение, получим: . Подставляя выражения для и в первое уравнение, получим: . Обозначив , а получим общее решение системы

Придавая свободным переменным любые значения, будем получать частные решения системы. Частным решением системы будет являться решение .

Вопросы для защиты работы

1. Однородные и неоднородные системы.

2. Совместные и несовместные системы.

3. Что называется решением системы?

4. Сформулировать теорему Кронекера-Капелли.

5. Что означает «исследовать систему уравнений»?

6. Что можно сказать о множестве решений системы линейных уравнений, если ранг матрицы этой системы и ранг расширенной матрицы равны нулю?

7. Фундаментальная система решений?

Список основной литературы

1. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: Учеб. Пособие для студентов втузов. В 2-х ч. Ч. Ι. – 4-е изд., испр. и доп. – М.: Высш. Шк., 1986. – 304 с.

2. Виленкин И. В., Гробер В. М. Высшая математика для студентов экономических, технических и естественно-научных специальностей / Серия «Учебники, учебные пособия». – Ростов н/Д: Феникс, 2002. – 416 с.

3. Линейная алгебра: Учебное пособие / Под ред. В.С. Зарубина, А. Л. Криценко. Вып. IV. М.: Изд-во МГТУ, 2001.

Лабораторная работа 1

Тема: Решение СЛАУ по формулам Крамера и методом Гаусса.

Теоретическое обоснование

Системы линейных алгебраических уравнений

Система линейных уравнений с переменными имеет вид:

(1)

12 Следующая ⇒