ИССЛЕДОВАНИЕ РЕЖИМОВ РАБОТЫ ЦЕПЕЙ

Лабораторная работа № 23

ИССЛЕДОВАНИЕ РЕЖИМОВ РАБОТЫ ЦЕПЕЙ

Синусоидального ТОКА

Цель работы: экспериментальное определение параметров пассивных элементов электрической цепи; исследование влияния переменного параметра (емкости конденсатора С) на величины тока и напряжения в неразветвленной цепи, исследование режима резонанса напряжений; исследование влияния переменного параметра (емкости конденсатора С) на величины токов в цепи с параллельным соединением катушки индуктивности и конденсатора, исследование режима резонанса токов; получение навыков построения векторных диаграмм по опытным данным.

Теоретические сведения

Синусоидальный ток. Основные понятия

Мгновенные значения синусоидальных тока и напряжения определяются выражениями

i(t)= I_m sin(ω t + ψ _i), u(t)= U_m sin(ω t + ψ _u),

где I_m, U_m – амплитудные значения тока и напряжения;

(ω t + ψ ) – фаза колебания, аргумент синусоидальной функции;

ω [рад/с] – угловая частота, которая может быть определена как ω =2π f = 2π /T;

f [Гц] – линейная частота; Т [c] – период колебаний;

ψ _i, ψ _u - начальные фазы тока и напряжения, которые отсчитываются от начала координат до ближайшей точки на оси абсцисс перехода синусоидальной функции через ноль от отрицательных к положительным ее значениям. Начальная фаза может быть положительной, отрицательной и равной нулю. При ψ > 0 начало синусоиды сдвинуто влево относительно начала координат, при ψ < 0 – вправо, а при ψ = 0 синусоида имеет начало в начале координат.

На рис. 3.1 построены временные графики мгновенных значений тока и напряжения одинаковой частоты:

i(t)= I_m sin(ω t + ψ _i), u(t)= U_m sin(ω t + ψ _u).

Угол, на который синусоида тока сдвинута относительно синусоиды напряжения, называют углом сдвига фаз φ и определяют его как разность начальных фаз напряжения и тока:

φ = ψ _u – ψ _i.

Рис. 3.1

Большинство измерительных приборов измеряют действующие значения токов и напряжений. Поэтому расчеты в цепях синусоидального тока чаще всего выполняются по действующим значениям, которые связаны с амплитудными следующими соотношениями:

, .

Изображение синусоидальных величин

Векторами и комплексными числами

Расчет цепей переменного тока существенно упрощается, если синусоидально изменяющиеся токи, напряжения, ЭДС и другие величины заменить их изображениями на комплексной плоскости (рис. 3.2)

где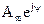

- называется комплексной амплитудой.

Комплексная амплитуда представляет собой вектор на комплексной плоскости, длина которого соответствует амплитудному значению синусоидальной функции А_m, а угол ψ – начальной фазе.

В курсе ТОЭ пользуются следующими темя формами записи комплексной амплитуды в виде комплексного числа:

показательная ;

тригонометрическая ;

алгебраическая .

где - действительная часть комплексного числа;

- мнимая часть комплексного числа,

Для обратного перехода от алгебраической к показательной форме записи необходимо найти модуль этого комплексного числа с помощью теоремы Пифагора (рис.3.2) и аргумент путем определения тангенса соответствующего угла:

, .

Алгебраическая форма удобна при сложении и вычитании комплексных величин, а показательная при умножении, делении, возведении в степень и извлечении корня.

Мнимая единица называется оператором поворота на угол . Умножение на сводится к повороту вектора против часовой стрелки на прямой угол, а умножение на - к повороту вектора на прямой угол по часовой стрелке.

Числа и

называют комплексно-сопряженными числами. Произведение комплексно-сопряженных чисел - действительное число, равное квадрату их модуля .

Комплексное действующее значение .

Все формы записи комплексной величины и связь между ними записываются

Векторная диаграмма представляет собой совокупность векторов токов и напряжений, построенных на комплексной плоскости.

Параллельное соединение реальной индуктивной

Катушки и конденсатора

На рис. 3.14 представлена схема параллельного соединения реальной индуктивной катушки с параметрами L_К, R_К и идеального конденсатора с емкостью С.

Для действующих комплексных значений токов на основании первого закона Кирхгофа запишем:

где активная и реактивные составляющие проводимостей

Ток реальной индуктивной катушки представлен как сумма активной составляющей, совпадающей по фазе с напряжением, и реактивной составляющей отстающей от напряжения по фазе на угол 90º. В этом случае на схеме замещения реальную индуктивную катушку можно представить в виде параллельного соединения двух ветвей с активной и реактивной проводимостями (рис. 3.15).

Заметим, что в случае, если ветвь содержит не один, а несколько элементов, активная и реактивная составляющие полной проводимости такой ветви будут определяться:

, .

Комплексная проводимость схемы рис. 3.14

Векторная диаграмма токов и напряжений (рис. 3.16) будет аналогична векторной диаграмме параллельного соединения идеальных элементов R, L, C.

Опытным путем

Параметры пассивных двухполюсников можно определить опытным путем с помощью амперметра, вольтметра и фазометра.

Рис. 3.17

Определим параметры индуктивной катушки. Насхеме замещения реальная катушка индуктивности изображена в виде последовательного соединения ее активного и реактивного сопротивлений. Для того чтобы определить активное сопротивление катушки R_к и ее индуктивность L_к, катушку и измерительные приборы подключают к сети переменного тока согласно схеме, показанной на рис. 3.17.

Определив по приборам действующие значения напряжения на зажимах цепи U, тока I и с помощью фазометра угол сдвига фаз φ _к между ними, рассчитаем модуль полного сопротивления катушки: , а также активную и реактивную составляющие этого сопротивления. Из треугольника сопротивлений (рис. 3.10) можно легко получить формулы для их определения:

активное сопротивление катушки

реактивное сопротивление катушки

Так как X_L = ω L=2π f, то индуктивность катушки определяется:

Аналогичным образом можно определить параметры схемы замещения конденсатора. Но так как потери в диэлектрике на низкой частоте невелики, то в данной лабораторной работе конденсатор будем считать идеальным с заданной емкостью С.

Программа работы

1. Определение параметров индуктивной катушки R_K, L_K:

а) собрать цепь лабораторной установки (рис. 3.20);

б) исключить из цепи емкостный элемент, для чего замкнуть накоротко клеммы батареи конденсаторов;

в) при двух значениях входного напряжения 80 и 100 В, устанавливаемых с помощью ЛАТра, измерить ток в цепи и угол сдвига фаз между напряжением на зажимах катушки и током. Измеренные значения занести в табл. 3.1;

г) по результатам измерений вычислить активное R_K и индуктивное X_K сопротивления катушки, а также ее индуктивность L. Данные расчетов занести в табл. 3.1;

Таблица 3.1

Измерено	Вычислено
U, B	I, A	φ _К, град	R_K, Ом	X_K, Ом	L, Гн
80 В
100 В
Среднее значение определяемых величин

2. Исследование влияния переменной емкости на свойства цепи с последовательным соединением катушки и конденсатора:

а) рассчитать значение резонансной емкости, используя значение индуктивности катушки из табл. 3.1;

б) убрать провод, закорачивающий клеммы батареи конденсаторов;

в) установить на входе цепи напряжение 20 В и далее поддерживать его неизменным;

г) изменяя емкость батареи конденсаторов, произвести 7 измерений величин, указанных в табл. 3.2, из них 3 опыта проводят при емкости меньше резонансной, 3 опыта при емкости больше резонансной, и особо необходимо отметить режим, наиболее близкий к резонансному; данные измерений занести в табл. 3.2.

Наиболее целесообразно выполнять исследования по п. 2, г следующим образом:

- изменяя емкость батареи конденсаторов вблизи рассчитанной величины С_Р, подобрать такое значение емкости, при котором в цепи наступит резонанс напряжений, то есть угол сдвига фаз, измеряемый фазометром, будет равен или близкий к нулю; измерить ток и напряжения на катушке и конденсаторе для этого режима;

- далее выполнить три опыта при емкости меньше резонансной, и три опыта – больше резонансной; шаг изменения емкости батареи конденсаторов принять 3-4 мкФ.

Таблица 3.2

№ опыта	Измерено	Вычислено
U, B	C, мкФ	I, А	U_K, В	U_C, В	φ, град	z, Ом	X, Ом	X_K, Ом	U_L, В
	20 B

3. Исследование влияния переменной емкости на свойства цепи с параллельным соединением катушки и конденсатора:

а) собрать цепь лабораторной установки рис. 3.21 с параллельным соединением катушки и конденсатора;

б) рассчитать значение резонансной емкости, используя значение индуктивности катушки из табл. 3.1;

в) установить на входе цепи напряжение 80 В и далее поддерживать его неизменным;

г) изменяя емкость батареи конденсаторов, произвести 7 измерений величин, указанных в табл. 3.3, из них 3 опыта проводят при емкости меньше резонансной, 3 опыта при емкости больше резонансной, и особо необходимо отметить режим, наиболее близкий к резонансному; данные измерений занести в табл. 3.3.

Порядок проведения опытов сохранять таким же, как и при выполнении эксперимента по п. 2, г.

4. Построение резонансных кривых.

а) для исследуемой схемы (рис. 3.20) по данным табл. 3.2 построить на миллиметровой бумаге на одном графике зависимости I(C), U_L(C), U_C(C), φ (C).

б) для исследуемой схемы (рис. 3.21) по данным табл. 3.3 построить на миллиметровой бумаге на одном графике зависимости I(C), I_L(C), I_C(C), φ (C).

Таблица 3.3

№ опыта	Измерено	Вычислено
U, B	C, мкФ	I, А	I_К, А	I_С, А	φ, град	C, мкФ
	80 B

5. Построение векторных диаграмм.

а) по данным табл. 3.2 построить векторные диаграммы токов и напряжений для трех режимов: X_L> X_C, X_L=X_C, X_L< X_C.

б) по данным табл. 3.3 построить векторные диаграммы токов и напряжений для трех режимов: b_L> b_C, b_L=b_C, b_L< b_C.

6. Сделать выводы по проделанной работе, обращая внимание насколько экспериментальные значения соответствуют теоретическим.