Изображение синусоидальных величин

Векторами и комплексными числами

Расчет цепей переменного тока существенно упрощается, если синусоидально изменяющиеся токи, напряжения, ЭДС и другие величины заменить их изображениями на комплексной плоскости (рис. 3.2)

где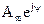

- называется комплексной амплитудой.

Комплексная амплитуда представляет собой вектор на комплексной плоскости, длина которого соответствует амплитудному значению синусоидальной функции А_m, а угол ψ – начальной фазе.

В курсе ТОЭ пользуются следующими темя формами записи комплексной амплитуды в виде комплексного числа:

показательная ;

тригонометрическая ;

алгебраическая .

где - действительная часть комплексного числа;

- мнимая часть комплексного числа,

Для обратного перехода от алгебраической к показательной форме записи необходимо найти модуль этого комплексного числа с помощью теоремы Пифагора (рис.3.2) и аргумент путем определения тангенса соответствующего угла:

, .

Алгебраическая форма удобна при сложении и вычитании комплексных величин, а показательная при умножении, делении, возведении в степень и извлечении корня.

Мнимая единица называется оператором поворота на угол . Умножение на сводится к повороту вектора против часовой стрелки на прямой угол, а умножение на - к повороту вектора на прямой угол по часовой стрелке.

Числа и

называют комплексно-сопряженными числами. Произведение комплексно-сопряженных чисел - действительное число, равное квадрату их модуля .

Комплексное действующее значение .

Все формы записи комплексной величины и связь между ними записываются

Векторная диаграмма представляет собой совокупность векторов токов и напряжений, построенных на комплексной плоскости.

Действия с комплексными числами

Пусть мы имеем два комплексных числа, записанных в показательной и алгебраической формах:

и .

Рассмотрим основные действия, выполняемые над комплексными числами.

Алгебраическое сложение комплексных чисел выполняется при записи их в алгебраической форме. При этом мы суммируем отдельно действительные части комплексных величин, отдельно - мнимые:

Умножение комплексных чисел удобнее всего выполнять в показательной форме записи. При этом модуль нового комплексного числа получается путем перемножения модулей комплексных величин, а аргумент – путем сложения фаз:

Деление комплексных величин выполняется аналогично. Для определения модуля новой комплексной величины, модуль числителя необходимо разделить на модуль знаменателя, а для определения аргумента необходимо из фазы числителя вычесть фазу знаменателя:

Возведение в степень n выполняется в показательной форме, для этого модуль комплексного числа возводят в соответствующую степень, а показатель просто умножают на n:

Извлечение корня n-ой степени равносильно возведению в степень 1/n:

Пример.

Записать в показательной и алгебраической формах напряжение В и ток А.

Решение. Комплексное действующее значение напряжения

Комплексное действующее значение тока

Пример. Записать в показательной форме следующие комплексные числа:

а) 3+j4; б) 3-j4; в) -3+j4; г) -3-j4.

Решение. Для наглядности при переводе из алгебраической формы записи комплексного числа в показательную удобно сопровождать вычисления построением векторов на комплексной плоскости. Необходимо помнить, что во всех случаях, когда действительная часть комплексного числа отрицательна, то при определении начальной фазы необходимо прибавить или отнять 180^°.

а) 3+j4=