
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Теорема Вариньона о моменте равнодействующей силы.Стр 1 из 8Следующая ⇒
Виды связей и их реакции Связями называются любые ограничения, препятствующие перемещению тела в пространстве. Виды связей и их реакции
|
| 2Вращательное движение вокруг неподвижной оси | |
Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения. Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' (рис. 2.12).
 Рис. 2.12
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr. При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная Рис. 2.12
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr. При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная  , ни вторая производная , ни вторая производная 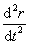 не могут служить характеристикой движения всего твердого тела. За это же время dt радиус-вектор не могут служить характеристикой движения всего твердого тела. За это же время dt радиус-вектор  , проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). Угол поворота dφ характеризует перемещение всего тела за время dt. Удобно ввести , проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). Угол поворота dφ характеризует перемещение всего тела за время dt. Удобно ввести  – вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора – вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора  и направление вращения связаны «правилом буравчика»). Элементарные повороты удовлетворяют обычному правилу сложения векторов: и направление вращения связаны «правилом буравчика»). Элементарные повороты удовлетворяют обычному правилу сложения векторов:
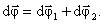 Угловой скоростью называется вектор
Угловой скоростью называется вектор  , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении  ( (  и и  всегда направлены в одну сторону). всегда направлены в одну сторону).
Если ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси.
В векторной форме
Введем вектор углового ускорения
Вектор
Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:
Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения. · равномерное вращение ε = 0; ω = const; φ = φ 0 ± ω t, · равнопеременное вращение |
4Теорема Вариньона ( теорема о моменте равнодействующей силы): момент равнодействующей относительно любой точки = геометрической сумме моментов составляющих сил относительно той же точки. Условия равновесия пространств. сист.сил:
å Fkx=0; å Fky=0; å Fkz=0; å Mx(Fk)=0; å My(Fk)=0; å Mz(Fk)=0. Условия равновесия для системы параллельных сил (||z): å Fkz=0; å Mx(Fk)=0; å My(Fk)=0. Центр параллельных сил — точка, через которую проходит линия действия равнодействующей системы ||-ых сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол. Координаты центра ||-ых сил: и т.д.
Условия равновесия пл. сист. сил: векторное: . аналитич:
, или
где А, В, С — точки, не лежащие на одной прямой, или, ось " х" не перпендикулярна отрезку АВ.
Равновесие тел при наличии трения. Закон Кулона (закон Амонта — Кулона): максимальная сила сцепления пропорциональна нормальному давлению тела на плоскость
, fсц — коэффициент сцепления (зависит от материала, состояния поверхностей, определяется экспер-но). Направление силы сцепления противоположно направлению того движения, которое возникло бы при отсутствии сцепления. При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Ее направление противоположно скорости тела, f —коэффициент трения скольжения (определяется опытным путем). f< fсц. Реакция шероховатой (реальной) поверхности в отличии от идеально гладкой имеет две составляющие: нормальную реакцию и силу сцепления (или силу трения при движении). Угол jсц—угол сцепления (jтр — угол трения) tgjсц=fсц (tgjтр=f). Конус с вершиной в точке касания тел, образующая которого составляет угол сцепления (угол трения) с нормалью к поверхностям тела назыв. конусом сцепления (конус трения). Для того чтобы тело начало движение, необходимо (и достаточно), чтобы равнодействующая активных сил находилась вне конуса трения. Трение качения — сопротивление, возникающее при качении одного тела по поверхности другого. Причина его появления в деформации катка и плоскости в точке их соприкосновения и смещения нормальной реакции в сторону возможного движения. Мтр= fkN — момент трения качения, fk — коэффициент трения качения; имеет размерность длины.
Рис.34
Рассмотрим круглый цилиндрический каток радиуса R и веса  , лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу
, лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу  (рис. 34, а), меньшую Fпр. Тогда в точке А возникает сила трения
(рис. 34, а), меньшую Fпр. Тогда в точке А возникает сила трения  , численно равная Q, которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию
, численно равная Q, которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию  тоже приложенной в точке А, то она уравновесит силу
тоже приложенной в точке А, то она уравновесит силу  , а силы
, а силы  и
и  образуют пару, вызывающую качение цилиндра. При такой схеме качение должно начаться, как видим, под действием любой, сколь угодно малой силы
образуют пару, вызывающую качение цилиндра. При такой схеме качение должно начаться, как видим, под действием любой, сколь угодно малой силы  .
.
Истинная же картина, как показывает опыт, выглядит иначе. Объясняется это тем, что фактически, вследствие деформаций тел, касание их происходит вдоль некоторой площадки АВ (рис. 34, б). При действии силы  интенсивность давлений у края А убывает, а у края В возрастает. В результате реакция
интенсивность давлений у края А убывает, а у края В возрастает. В результате реакция  оказывается смещенной в сторону действия силы
оказывается смещенной в сторону действия силы  . С увеличением
. С увеличением  это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара (
это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара (  ,
,  ) с моментом
) с моментом  и уравновешивающая ее пара (
и уравновешивающая ее пара (  ) с моментом Nk. Из равенства моментов находим
) с моментом Nk. Из равенства моментов находим  или
или 
Пока  , каток находится в покое; при
, каток находится в покое; при  начинается качение.
начинается качение.
Входящая в формулу линейная величина k называется коэффициентом трения качения. Измеряют величину k обычно в сантиметрах. Значение коэффициента k зависит от материала тел и определяется опытным путем.
Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.
Для вагонного колеса по рельсу k=0, 5 мм.Рассмотрим движение ведомого колеса.  Качение колеса начнется, когда выполнится условие QR> M или Q> Mmax/R=kN/RСкольжение колеса начнется, когда выполнится условие Q> Fmax=fN.Обычно отношение
Качение колеса начнется, когда выполнится условие QR> M или Q> Mmax/R=kN/RСкольжение колеса начнется, когда выполнится условие Q> Fmax=fN.Обычно отношение  и качение начинается раньше скольжения.Если
и качение начинается раньше скольжения.Если  , то колесо будет скользить по поверхности, без качения.
, то колесо будет скользить по поверхности, без качения.
Отношение  для большинства материалов значительно меньше статического коэффициента трения
для большинства материалов значительно меньше статического коэффициента трения  . Этим объясняетсято, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катки, шариковые подшипники и т. п.).
. Этим объясняетсято, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катки, шариковые подшипники и т. п.).
трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Вследствие деформации тел их касание происходит вдоль площадки AB (рисунок 2.4, а), появляется распределенная система сил реакции (рисунок 2.4, б), которая может быть заменена силой и парой (рисунок 2.4, в).
Сила раскладывается на две составляющие – нормальную и силу трения скольжения. Пара сил называется моментом сопротивления качению Mc.

Рисунок 2.4
При равновесии тела момент сопротивления качению определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения.
Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством
Mcmax = Nδ ,
где δ – коэффициент трения качения, имеет размерность длины [м], зависит от материала контактирующих тел и геометрии зоны контакта.
Различают:
чистое качение – точка A (рисунок 2.4) не скользит по неподвижной плоскости;
качение со скольжением – наряду с вращением катка присутствует и проскальзывание в месте контакта, т.е. точка A движется по плоскости;
чистое скольжение – каток движется по плоскости, не имея вращения (см. п.2.1).
Для того, чтобы каток не скользил, необходимо условие Fтр < Fтр max < fN; чтобы каток не катился – Mc < Mcmax = δ N.
Также существует трение верчения – когда активные силы стремятся вращать тело вокруг нормали к общей касательной поверхности соприкосновения.
Основная теорема статики

Пусть дана произвольная система сил (F1, F2,..., Fn). Сумму этих сил F=å Fk называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса.
Осн теор статики (теорема Пуансо ): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. Пусть О — центр приведения, принимаемый за начало координат, r1, r2, r3, …, rn–соответствующие радиусы-векторы точек приложения сил F1, F2, F3, ..., Fn, составляющих данную систему сил (рис. 4.2, а). Перенесем силы F1, Fa, F3, ..., Fn в точку О. Сложим эти силы как сходящиеся; получим одну силу: Fо=F1+F2+…+Fn=å Fk, которая равна главному вектору (рис. 4.2, б). Но при последовательном переносе сил F1, F2,..., Fn в точку О мы получаем каждый раз соответствующую пару сил (F1, F”1), (F2, F”2),..., (Fn, F" n).Моменты этих пар соответственно равны моментам данных сил относительно точки О: М1=М(F1, F”1)=r1 x F1=Мо(F1), М2=М(F2, F”2)=r2 x F2=Мо(F2), …, Мп=М(Fn, F" n)=rn x Fn=Мо(Fn). На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т. е. равен главному моменту, так как согласно формулам (3.18) и (4.1) имеем (рис. 4.2, в) М0=М1+М2+...+Мn=Мо(F1)+Мо(F2)+…+ Мо(Fn)==å Мо(Fk)=å rk x Fk. Систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой Fo=å Fk (4.2) и парой сил с моментом M0=å M0(Fk)=å rk x Fk. (4.3). В технике очень часто проще задать не силу или пару, а их моменты. Например, в характеристику электромотора входит не сила, с которой статор действует на ротор, а вращающий момент.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектораколичества движения  рассматривают его момент относительно некоторого центра или оси.
рассматривают его момент относительно некоторого центра или оси.
Эти моменты определяются так же, как и моменты силы (см. § 8, 14 и 28).
Таким образом, моментом количества движения точки относительно некоторого центра О называется векторная величина то  определяемая равенством
определяемая равенством
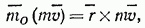
где 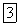 — радиус-вектор движущейся точки, проведенный из центра О.
— радиус-вектор движущейся точки, проведенный из центра О.
При этом вектор  направлен перпендикулярно плоскости, проходящей через
направлен перпендикулярно плоскости, проходящей через  и центр
и центр  (рис. 224; для сравнения на нем показан и вектор
(рис. 224; для сравнения на нем показан и вектор  ).
).
Момент количества движения точки относительно какой-нибудь оси  проходящей через центр О, будет равенпроекции вектора
проходящей через центр О, будет равенпроекции вектора  на эту ось:
на эту ось:
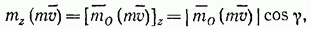
где  — угол между вектором
— угол между вектором  и осью Oz.
и осью Oz.
Теорема моментов устанавливает, как изменяется со временем вектор  . Чтобы доказать ее, продифференцируем по времени выражение (35). Получим
. Чтобы доказать ее, продифференцируем по времени выражение (35). Получим
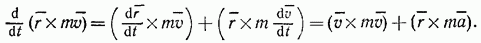
Но  как векторное произведение двух параллельных векторов,
как векторное произведение двух параллельных векторов,  , где при действии нескольких сил
, где при действии нескольких сил  . Следовательно,
. Следовательно,
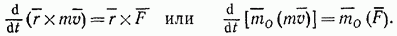
В результате мы доказали следующую теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.
Сравнивая уравнения (37) и (32), видим, что моменты векторов  и F связаны такой же зависимостью, какой связаны сами векторы
и F связаны такой же зависимостью, какой связаны сами векторы 
Если спроектировать обе части равенства (37) на какую-нибудь ось  проходящую через центр О, то, учтя соотношение (36), получим
проходящую через центр О, то, учтя соотношение (36), получим
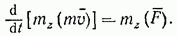
Это равенство выражает теорему моментов относительно оси.
Из уравнения (37) следует, что если  то
то  , т. е. если момент действующей силы относительно некоторого центра равен нулю, то момент количества движения точки относительно этого центра есть величина постоянная. Такой результат имеет место в практически важном случае движения под действием центральной силы (см. § 86).
, т. е. если момент действующей силы относительно некоторого центра равен нулю, то момент количества движения точки относительно этого центра есть величина постоянная. Такой результат имеет место в практически важном случае движения под действием центральной силы (см. § 86).
 Рис. 224
Рис. 224 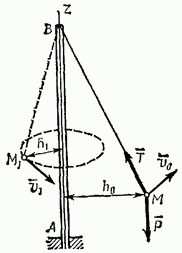
Рис. 225
Связи и их реакции
Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.
Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.
Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.
Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.
3.1.
3.2.
Пара сил. Момент пары
Система двух равных по модулю, параллельных и противоположно направленных сил  и
и  называется парой сил.Система не находится в равновесии, но и не имеет равнодействующей.Плоскость, проходящая через линии действия сил называют плоскостью действия пары ( рис. 24
называется парой сил.Система не находится в равновесии, но и не имеет равнодействующей.Плоскость, проходящая через линии действия сил называют плоскостью действия пары ( рис. 24  ).Расстояние d между линиями действия сил пары называют плечом пары.Действие пары сил на твердое тело сводится к вращательному эффекту и зависит от:
).Расстояние d между линиями действия сил пары называют плечом пары.Действие пары сил на твердое тело сводится к вращательному эффекту и зависит от:
1) модуля F и длины плеча d;
2) положения плоскости пары;
3) направления поворота в этой плоскости.
Для характеристики этого вращательного эффекта вводится понятие момент пары.
Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо.

Момент пары условимся считать положительным (+), если пара стремится повернуть тело против хода часовой стрелки, и отрицательным (-) - когда по ходу часовой стрелки.
Обозначение момента пары m или М без индекса имеет свой смысл, так как момент пары нельзя смешивать с моментом силы относительно центра и этот центр указывается в индексе (например:  ). Момент же пары определяется только силами и плечом.
). Момент же пары определяется только силами и плечом.
Действие пары сил, как уже указывалось выше, характеризуется тремя условиями. При характеристике пар необходимо задавать все три значения. Но мы знаем, что вектор-нормаль к плоскости задает значения второго и третьего условия. Если мы теперь пронормируем вектор-нормаль значением момента пары, то все три условия будут выполнены. Эти соображения и позволили рассматривать момент пары как вектор.
Будем изображать момент пары вектором  или
или 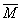 , модуль которого равен модулю момента пары, и который направлен перпендикулярно плоскости действия пары, в ту сторону откуда поворот пары виден происходящим против хода часовой стрелки ( рис. 25
, модуль которого равен модулю момента пары, и который направлен перпендикулярно плоскости действия пары, в ту сторону откуда поворот пары виден происходящим против хода часовой стрелки ( рис. 25  ).
).
Если рассматривать только пары лежащие в одной плоскости, то вместо вектора момента пары, можно стрелкой указывать только направлением поворота.
Вектор  на рис. 25 условно изображен выходящим из точек В и D, однако он может изображаться выходящим из середины АВ или CD или из произвольной точки плоскости действия пары, так как
на рис. 25 условно изображен выходящим из точек В и D, однако он может изображаться выходящим из середины АВ или CD или из произвольной точки плоскости действия пары, так как

3.3.
Основное уравнение динамики
| 1. | F= ma |
, или в векторной форме
| 2. |
= m
|
Единица СИ силы:
| 3. | [F]= нютон(Н)= кг ·
|
Сила, определение
Силой в один ньютон называется такая сила, которая сообщает телу массой 1 (кг) ускорение 1 (м/с² ).
44. Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма.
Вид уравнений[править | править вики-текст]
Если голономная механическая система описывается лагранжианом 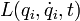 (
( 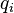 — обобщённые координаты, t — время, точкой обозначено дифференцированиепо времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
— обобщённые координаты, t — время, точкой обозначено дифференцированиепо времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
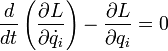
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы.
Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид

где 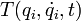 — кинетическая энергия системы,
— кинетическая энергия системы, 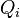 — обобщённая сила.
— обобщённая сила.
Вывод уравнений[править | править вики-текст]
Уравнения Лагранжа в механике получаются из законов динамики Эйлера (баланса количества движения и момента количества движения) при определенных ограничениях на систему (в ней должны присутствовать лишь идеальные голономные связи). Для других случаев получаются модификации уравнений Лагранжа. Отметим, что это частный (хотя и очень важный) случай механических систем.
Если для рассматриваемой системы применим принцип наименьшего действия, то вывод можно провести иначе. В лагранжевой механике вывод уравнений Лагранжа происходит на основе принципа наименьшего действия. Механическая система может быть описана некой функцией 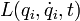 , называемой лагранжианом. Лагранжиан - это разность кинетической и потенциальной энергий системы. Принцип наименьшего действия гласит, что функционал
, называемой лагранжианом. Лагранжиан - это разность кинетической и потенциальной энергий системы. Принцип наименьшего действия гласит, что функционал
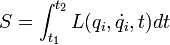
называемый действием принимает минимальное значение на траектории системы (здесь t1 и t2 — начальный и конечный моменты времени). Заметим, что необходимо доказать применимость принципа наименьшего действия к рассматриваемой системе: далеко не все физические системы ему подчиняются. Применяя к функционалу действию стандартную схему оптимизации, получаем для него уравнения Лагранжа — Эйлера, которые и называются уравнениями Лагранжа второго рода для механической системы.
Вывод уравнений для системы с одной обобщенной координатой и скоростью

Изменение действия при переходе из состояния  в
в 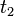

Разлагая эту разность по степеням

Варьируя это выражение, получаем:

Первое слагаемое заменяется по формуле Ньютона-Лейбница. Второе интегрируем по частям замечая что 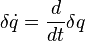
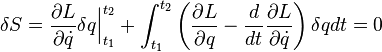
Первое слагаемое равно нулю исходя из самой первой формулы вывода. Второе слагаемое может быть равно нулю только если подынтегральное выражение равно нулю. Оно и является искомым уравнением Лагранжа:
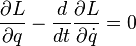
Виды связей и их реакции
Связями называются любые ограничения, препятствующие перемещению тела в пространстве.
Тело, стремясь под действием приложенных сил осуществить переме-щение, которому препятствует связь, будет действовать на нее с некоторой силой, называемой силой давления на связь. По закону о равенстве действия и противодействия, связь будет действовать на тело с такой же по модулю, но противоположно направленной силой.
Сила, с которой данная связь действует на тело, препятствуя тем или иным перемещениям, называется силой реакции (реакцией) связи.
Одним из основных положений механики является принцип освобождаемости от связей: всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями связей. Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. Основные виды связей и их реакции приведены в таблице 1.1.
Виды связей и их реакции
Последнее изменение этой страницы: 2016-05-29; Просмотров: 1000; Нарушение авторского права страницы